
- •Численные методы (Методические указания и задания)
- •Численное интегрирование
- •1. 1. Метод прямоугольников
- •1. 2. Метод трапеций
- •1. 3. Метод парабол (метод Симпсона)
- •Приближенное решение алгебраических и трансцендентных уравнений
- •2. 1. Уточнение корней методом половинного деления
- •2. 2. Метод итераций
- •2. 3. Метод хорд
- •2. 4. Метод касательных (Метод Ньютона)
- •2. 5. Комбинированный метод хорд и касательных
- •Аппроксимация функций
- •3. 1. Математическая постановка задачи интерполирования
- •3. 2. Интерполяционный многочлен Лагранжа
- •3. 3. Линейная интерполяция
- •3. 4. Метод наименьших квадратов
- •3. 5. Нахождение параметров линейной функции
- •3. 6. Нахождение параметров квадратичной функции
- •Решение систем линейных уравнений
- •Содержание
2. 1. Уточнение корней методом половинного деления
Пусть корень
уравнения
![]() отделен на отрезке[a,
b],
т.е. f(a)f(b)<0
и f
’(x)
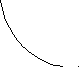
сохраняет знак (рис. 2.6.).
отделен на отрезке[a,
b],
т.е. f(a)f(b)<0
и f
’(x)
сохраняет знак (рис. 2.6.).


b
c0
x a
c1



Рис. 2.6
В качестве начального
приближения корня возьмем точку c0
– середину отрезка:
![]() .
Еслиf(с0)=0,
то c0
– искомый корень уравнения, если
.
Еслиf(с0)=0,
то c0
– искомый корень уравнения, если
![]() ,
то из двух отрезков[a,
c0]
и [c0,
b]
выбираем тот, на концах которого функция
принимает значение разных знаков.
,
то из двух отрезков[a,
c0]
и [c0,
b]
выбираем тот, на концах которого функция
принимает значение разных знаков.
Новый отрезок опять делим пополам и далее поступаем аналогично вышеизложенному. Длина каждого нового отрезка вдвое меньше длины предыдущего отрезка, т.е. за n шагов сократится в 2n раз.
Вычисления
прекращаем, если длина отрезка![]() станет меньше заданной погрешности
станет меньше заданной погрешности![]() ,
т.е.
,
т.е.![]() .
.
Блок-схема метода половинного деления



ВЫЧИСЛЕНИЕ СЕРЕДИНЫ ОТРЕЗКА c=(a+b)/2

ВЫЧИСЛЕНИЕ f(c)


f(c)f(a)<0

нет

b=c
a=c



нет![]()
да
a,
b


КОНЕЦ
2. 2. Метод итераций
Решение уравнения
вида
![]() методом итераций состоит в выборе
начального приближения значенияx0
и последовательном вычислении
методом итераций состоит в выборе
начального приближения значенияx0
и последовательном вычислении
x1=f(x0);
x2=f(x1)
и т.д.
Если производная
f
’(x)
удовлетворяет условию
![]() ,
то последовательностьxi
сходится к исходному корню.
,
то последовательностьxi
сходится к исходному корню.
При реализации метода итераций на ЦВМ, исходя из предположения, что метод может не сойтись, необходимо предусмотреть в программе следующие условия окончания работы:
Останов, как только
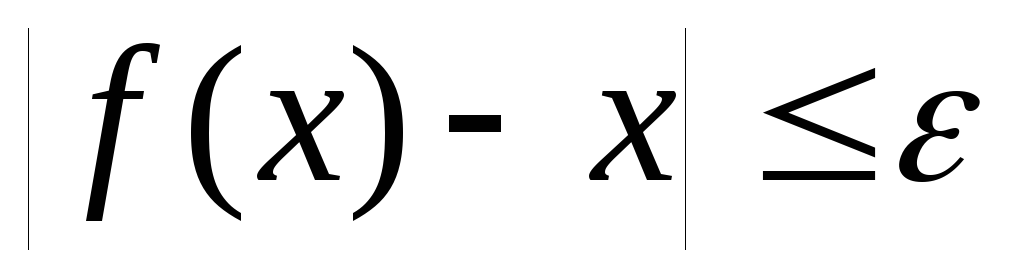 .
.Останов, как только число итераций достигнет N.
Величины
![]() иN
задаются.
иN
задаются.
2. 3. Метод хорд
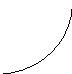
Пусть на отрезке [a, b] функция f(x) непрерывна, принимает на концах отрезка значение разных знаков, а производная f ’(x) сохраняет знак. В зависимости от знака второй производной возможны следующие случаи расположения кривых (рис. 2.7., 2.8):
f(a)<0, f(b)>0, f ‘(x)>0 – функция возрастает
а) f ’’(x)>0 (кривая вогнута вниз) б) f ’’(x)<0 (кривая вогнута вверх)
y y




a a
x b b x




Рис. 2.7
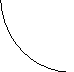
f(a)>0, f(b)<0, f ‘(x)<0 – функция убывает
а) f ’’(x)>0 б) f ’’(x)<0
y y



b b
x a a x




Рис. 2.8
Рассмотрим случай, когда f ’(x) и f ’’(x) имеют одинаковые знаки. (рис. 2.9.)
f(a)<0, f(b)>0, f ‘(x)>0 – функция возрастает
а) f ’’(x)>0 (кривая вогнута вниз) б) f ’’(x)<0 (кривая вогнута вверх)
y
в


 f(a)<0,
f(b)>0
f(a)<0,
f(b)>0
f ‘(x)>0, f ’’(x)>0
a
x1
x b
x2 ξ


A0
A1
Рис. 2.9
График функции проходит через точки A0(a, f(a)) и B(b, f(b)). Искомый корень уравнения (точка ξ) нам известен, вместо него возьмем точку x1 пересечения хорды A0B с осью абсцисс это и будет приближенное значение корня.
Уравнение хорды
A0B:
![]() .
.
Найдем значение x=x1, для которого y=0
![]() .
.
Теперь корень находится на отрезке [x1, b]. Применим метод хорд к этому отрезку. Проведем хорду, соединяющую точки A1(x1, f(x1)) и B и найдем точку x2 – точку пересечения хорды A1B с осью ox
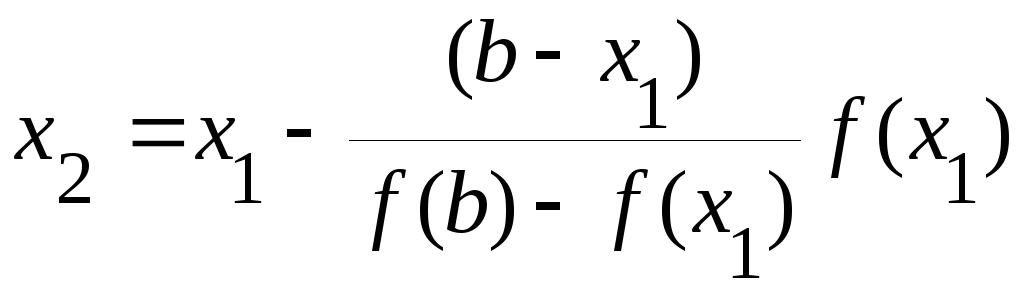 ,
,
Продолжая этот процесс, находим:
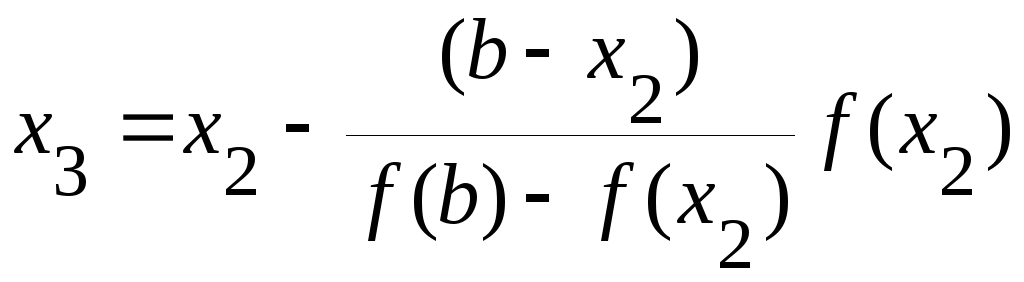 и т.д.
и т.д.
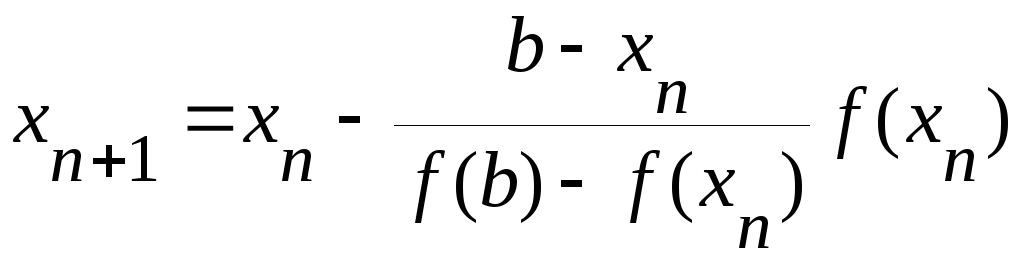 (2.2)
(2.2)
В этом случае конец b отрезка [a, b] остается неподвижным, а конец a перемещается.
Формула (2.2) носит название формулы метода хорд.
Вычисление по
формуле (2.2) продолжаем до тех пор, пока
не достигнем заданной точности, т.е.
должно выполняться условие:
![]() ,
где
,
где![]() - заданная погрешность.
- заданная погрешность.
Теперь рассмотрим случай, когда первая и вторая производные имеют разные знаки, т.е. f ‘(x) f ’’(x)<0 (рис. 2.10).
y
в
B0
B1



a
x2 ξ
x b
x1

A
Рис. 2.10
Соединим точки A(a, f(a)) и B0(b, f(b)) хордой AB0. Точку пересечения хорды AB0 с осью ox будем считать первым приближением корня. В этом случае, очевидно, неподвижным концом отрезка будет являться конец a.
Запишем уравнение хорды AB0:
![]()
Отсюда найдем x1,
полагая y=0:
![]() .
.
Теперь корень
![]() .
Применяя метод хорд к отрезку, получим
.
Применяя метод хорд к отрезку, получим
 (2.3)
(2.3)
Условие окончания
вычислений:
![]() .
.
Итак, если f ‘(x) f ’’(x)>0 приближенное значение корня находят по формуле (2.2), если f ‘(x) f ’’(x)<0, то по формуле (2.3).
Практически выбор той или иной формулы осуществляют, пользуясь следующим правилом: неподвижным концом отрезка является тот, для которого знак функции совпадает со знаком второй производной.
