книги / Строительная механика стержневых систем. Ч. 2

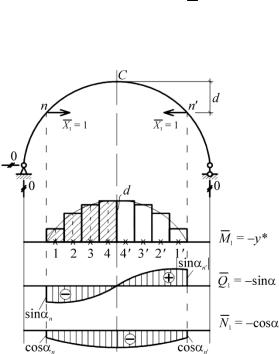
Для стрельчатой арки на эпюре Q1 в сечении С скачок

Рис. 9.8

Например, для сечения k с координатами хk , уk величина уk* показананарис. 9.7, аиопределяетсяпоформуле уk* уk ( f d).

Грузовые эпюры представлены на рис. 9.5. По методу сил

11 Х1 1Р 0 .

31

где Nзат Х1 1 (усилие в затяжке единичного состояния). Заменим криволинейные интегралы определенными по

длине затяжки, а затем перейдем к сумме (см. п. 9.1.2).

32

1P M1MP ds,

S EJ

где N1 – эпюра продольных сил единичного состояния основной системы.

мент инерции сечения в ключе.

x lтзат ,

где m – число интервалов, на которые делим ту часть арки, что выше затяжки, и ее горизонтальную проекцию.

По формулам метода сил получим формулы определения усилий в арке с повышенной затяжкой.

Для сечений арки ниже затяжки, например, k1 хk1, уk1 , и углом наклона касательной в сечении арки к горизонтали k1

33

Для сечений арки выше затяжки, например, k xk , yk , как на рис. 9.7, а, и углом наклона касательной в сечении арки к горизонтали k

Nk NkP Х1 cos k .

В сечениях n и n′, где примыкает затяжка, на эпюрах Q и N будут скачки, так как

Qnлев QnP ; Qnправ QnP X1 sin n ,

Эпюры M, Q и N строят относительно оси арки.

Проверка окончательной эпюры изгибающих моментов основана на отрицании взаимного перемещения любого сечения затяжки по ее направлению, т.е.

34

После преобразований получим

35

ГЛАВА 10. РАСЧЕТ СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫХ СИСТЕМ

МЕТОДОМ ПЕРЕМЕЩЕНИЙ

10.1. Неизвестные метода перемещений

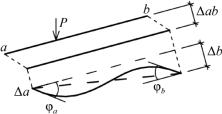
Вырежем из стержневой системы отдельный стержень с упруго закрепленными концами (рис. 10.1).

Рис. 10.1

Под действием нагрузки и концевых усилий стержень деформируется. Влиянием продольных сил на перемещения и изменением длины стержня за счет изгиба его оси пренебрегают, как и в методе сил.

1.Стержень а–b может совершать поступательное перемещение. Это ∆аb на рис. 10.1. При поступательном перемещении стержень не деформируется (не изгибается), следовательно, внутренние усилия не возникают. Поступательное перемещение не принимается за неизвестное перемещение метода перемещений.

2.Возможны перемещения одного из концов стержня, например конца «а» на величину ∆а и конца «b» на величину ∆b,

внаправлении, перпендикулярном стержню. При этом линейные смещения ∆а и ∆b не являются зависимыми и принимаются за неизвестные перемещения концов стержня.

3.Левый конец стержня при неподвижном правом может поворачиваться на величину угла φа.

36

4.Правый конец стержня при неподвижном левом может поворачиваться на величину угла φb.

5.Стержень аb деформируется и от нагрузки, к нему приложенной.

Углы поворота концов стержня (φа, φb) независимые. Независимые перемещения концов стержня и принимают за неизвестные метода перемещений.

Линейные смещения и углы поворота узлов, где сходятся несколько стержней, равны.

10.2. Степень кинематической неопределимости

Степенью кинематической неопределимости (пкин) называется сумма независимых линейных и угловых перемещений узлов.

где пу – число независимых углов поворота; пл – число независимых линейных смещений узлов.

пу определяется по числу свободных (не прикрепленных к массиву) жестких узлов системы.

пл определяется по шарнирной схеме системы, полученной из заданной путем введения полных шарниров во все узлы, в том числе и опорные. Степень линейной подвижности (пл) равна степени свободы (w) такой шарнирной схемы, т.е.

где у – число узлов шарнирной схемы, в том числе и опорных; С – число стержней шарнирной схемы, в том числе и опорных.

Значит, определяя число линейных смещений узлов (пл) по формуле (10.2), мы, по существу, определяем степень подвижности (w) шарнирной схемы. А получив w = 0 или w < 0, необходимо проверить, правильно ли расставлены связи, правильно ли соединены диски шарнирной схемы. Если установим, что шарнирная схема геометрически неизменяемая, т.е. неподвиж-

ная, то пл 0 .

37

Если окажется, что при w = 0 или w < 0 шарнирная схема подвижная, т.е. геометрически изменяемая, то необходимо добавить кинематические связи (опорные стержни), препятствующие установленным перемещениям узлов. Это количество связей и определяет пл.

Таким образом, число линейных перемещений равно числу опорных связей (стержней), которые необходимо установить, чтобы обратить шарнирную схему в геометрически неизменяемую (неподвижную).

Будем различать два вида рам по их шарнирной схеме:

–рамы с несмещающимися узлами, шарнирная схема которых геометрически неизменяемая, т.е. пл 0;

–рамы со смещающимися узлами, шарнирная схема которых геометрически изменяемая система, т.е. пл 0 .

Рамы с несмещающимися узлами (несвободные рамы), как правило, проще рассчитывать методом перемещений.

10.3. Основная система метода перемещений

Основную систему образуют путем закрепления узлов заданной системы дополнительными связями против всех узловых перемещений. В жесткие узлы (кроме жестких опорных) вводятся фиктивные заделки, препятствующие повороту узлов, а в смещающиеся узлы вводятся опорные стержни, препятствующие их линейному перемещению по направлению возможного перемещения.

Фиктивные заделки изображают так:

Число дополнительных связей должно быть равно степени кинематической неопределимости системы.

В фиктивных заделках реакциями являются моменты (реактивные моменты), а в опорных стержнях силы (реактивные си-

38

лы). Неизвестные перемещения (углы поворота и линейные смещения узлов) обозначаются как Zi.

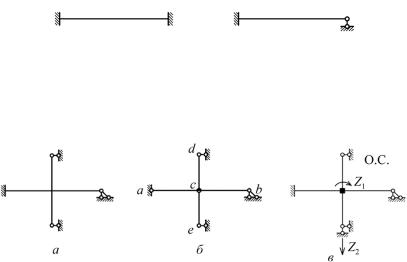
Основных систем можно составить множество, так как любые сечения можно принять за узел, но рациональной системой является единственный вариант. Основная система метода перемещений рассматривается как совокупность статически неопределимых балок (рис. 10.2):

Рис. 10.2

10.4. Примеры определения пкин и основной системы Задача 10.1

Определяем степень кинематической неопределимости по формуле 10.1:

nкин nу nл.

nу 1, так как один жесткий узел, nл 2у С 2 5 (4 6) 0

(по шарнирной схеме).

Проверяем шарнирную систему (рис. б) на геометрическую неизменяемость.

Рассмотрим в шарнирной схеме два диска ас и сb. Они образуют мгновенно изменяемую систему, перемещению точки с по вертикали не препятствует ни стержень cd, ни стержень сe,

39

т.е. нет закрепления узла с от перемещения по вертикали. Чтобы обратить шарнирную систему в неподвижную, необходимо добавить одну вертикальную связь (достаточно одной вертикальной связи) в узел d или только в узел е. Тогда надо принять

nл 1 и nкин 1 1 2 (основная система на рис. в).

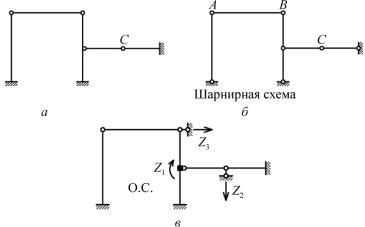
Задача 10.2.

По формуле (10.1) получим nкин 1 2 , так как nу 1 (один жесткий узел заданной системы), nл 2 , по формуле (10.2).

В шарнирной схеме 7 узлов и 12 стержней. Геометрическая изменяемость шарнирной схемы определяется подвижностью ригеля АВ по горизонтали и узла С по вертикали.

Значит, вводим в жесткий узел заданной рамы фиктивную заделку, препятствующую повороту на угол Z1, вертикальный опорный стержень, препятствующий линейному смещению узла С по вертикали на величину Z2 и горизонтальный опорный стержень, препятствующий перемещению узлов ригеля АВ на величину Z3. Основная система на рис. в.

40