книги / Прикладной статистический анализ в горном деле (Одномерная математическая статистика и регрессионный анализ)

3.3. Статистические критерии

3.3.1. Общие сведения

Как указывалось ранее, проверку статистических гипотез осуществляют при помощи так называемых статистических критериев. Статистический критерий – это строгое математическое правило, по которому гипотеза принимается или отвергается [1]. В статистике разработано множество критериев. Одни позволяют оценить различия в средних, полученных в двух выборках. Другие дают возможность оценить сходство или различие дисперсий в этих выборках. В регрессионном анализе используются критерии нормальности, критерии выбросов. Применяются статистические критерии и для оценки взаимодействия двух и более факторов в их влиянии на изменения признака. Критерии согласия проверяют, согласуется ли выборка с заданным распределением генеральной совокупности. Критическая область – область отвержения нулевой гипотезы. Вид критической области зависит от типа альтернативной гипотезы.

3.3.2. Критическая область

Критическая область – такая область пространства размещения выборочных данных, при попадании в которую нулевая гипотеза отклоняется. Требуемый уровень значимости α, который задается исследователем, определяет границу попадания в критическую область при верной нулевой гипотезе.

В практике могут встретиться несколько видов критических областей, на рис. 3.1 и 3.2 они заштрихованы. Мы должны выбрать рекомендованную для проверки статистику критерия. Все возможные значения её делятся на две непересекающиеся группы.

Первая группа содержит значения статистики критерия, при которых H0 отклоняется.

71

В любом случае выбранный критерий должен представлять такое условие, которое бы обеспечило принятие истинной и отклонение ложной гипотезы с высокой вероятностью. В большинстве случаев для того, чтобы мы признали различия значимыми, необходимо, чтобы эмпирическое значение критерия превышало критическое, хотя есть критерии (например, критерий Манна – Уитни или критерий знаков), в которых используются противоположные правила.

Критическое значение – пороговое значение статистики, которое ожидается в случае, если нулевая гипотеза верна. Критическое значение статистики отделяет область типичных значений статистики от критической области – области редких значений статистики при условии, что нулевая гипотеза верна. Область типичных значений – область неотвержения нулевой гипотезы.

Вторая группа – значения, при которых нулевая гипотеза принимается.

Например, на руднике имеются 60 замеров мощности пласта по выработкам блока. Замеры производились при наличии складок. Значения мощности (выборку) нормировали в отклонениях от среднего по стандарту. Необходимо определить наличие выбросов в замерах мощности при условии, что выборка подчиняется нормальному закону распределения с нулевым средним и некоторой дисперсией. Гистограмма распределения нормированной мощности показана на рис. 3.1. Среднее значение мощности равно 0, дисперсия равна 1. В связи с малым объёмом выборки выбросами будем считать мощности, выходящие за пре-

делы интервала x 2 . На гистограмме центральную часть

занимает область типичных значений нормированной мощности. Поскольку среднее равно нулю, эта область лежит в интервале от 2 до 2 . За границами типичных значений норми-

рованной мощности (слева и справа) лежат области редких значений при условии, что нулевая гипотеза о подчинении выборки нормальному закону распределения верна. Они и именуются

72

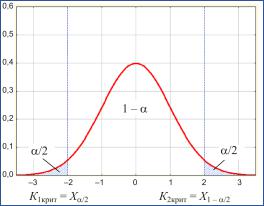
критическими областями, от области типичных значений нормированной мощности их отделяют критические значения.

Левая критическая область лежит в интервале (– ∞; – 2 ), далее (правее по рис. 3.1) располагается область типичных значений нормированной мощности, после которой находится правая критическая область. Она ограничена интервалом (+2 ; + ∞).

Область типичных значений именуется областью принятия гипотезы. Обычно критическая область и область принятия гипотезы – это интервалы. Также существуют точки, разде-

ляющие эти интервалы. Такие точки K1крит и K2крит на рис. 3.1, отделяющие критическую область от области принятия, назы-

ваются критическими точками. Примем Кэмп – эмпирическое (вычисленное) значение критерия. Областью допустимых значений (или областью принятия нулевой гипотезы H0) называют совокупность значений критерия Ккрит , при которых нулевая

гипотеза H0 не отклоняется [1].

Рис. 3.1. Двусторонняя критическая область

73

Критической областью называют совокупность значений критерия Ккрит , при которых нулевая гипотеза H0 отклоняется в

пользу конкурирующей (альтернативной) Н1 .

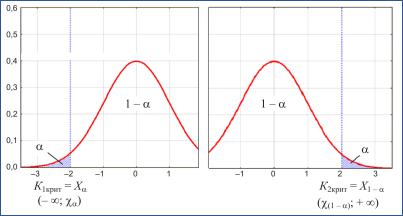
Рис. 3.2. Односторонние критические области:

а– левосторонняя, б – правосторонняя

Впримере на рис. 3.1 приведен вариант с двусторонними критическими областями. При проверке некоторых гипотез используется и односторонняя критическая область, которая может быть правосторонней или левосторонней (рис. 3.2).

1) Если конкурирующая гипотеза правосторонняя, то и критическая область правосторонняя (рис. 3.2, б). Интервал на

числовой оси, определяемый неравенством Kэмп K2крит, назы-

вается правосторонней критической областью. На рис. 3.2, б такая область лежит в интервале от х1 – α до + ;

2) Если конкурирующая гипотеза левосторонняя, то и критическая область левосторонняя. Интервал на числовой оси, определяемый неравенством Kэмп K1крит, называется левосто-

ронней критической областью, соответственно она лежит в интервале от – до хα;

74

3) Если конкурирующая гипотеза двусторонняя, то и критическая область двусторонняя (см. рис. 3.1). При двусторонней конкурирующей гипотезе определяются две критические точки (К1крит и К2крит ). На рис. 3.1 таких интервалов два. Интервалы,

определяемые неравенствами К1эмп < К1крит , К2эмп > К2крит , где (К2крит >К1крит ), составляютдвустороннююкритическуюобласть.

3.3.3. Основные принципы проверки статистических гипотез

Каждый тип статистических гипотез проверяется с помощью соответствующего критерия, являющегося наиболее мощным для конкретного случая. Например, для проверки гипотезы о виде закона распределения случайной величины используются критерии согласия Пирсона, Колмогорова – Смирнова и др. [19; 32; 60]. Проверка гипотезы о равенстве неизвестных значений дисперсий двух генеральных совокупностей выполняется с помощью критерия Фишера F. Гипотезы о неизвестных значениях параметров генеральных совокупностей проверяются с помощью критерия Z – нормальной распределенной случайной величины и критерия t-Стьюдента [20]. В п. 3.4 приведены примеры использования этих и других критериев для проверки статистических гипотез.

В общем случае пусть K (Х) – статистика, используемая при проверке некоторой нулевой гипотезы H0. Предполагается, что если нулевая гипотеза справедлива, то распределение этой статистики известно (формула (2.1)).

Величина критерия, рассчитываемая по специальным правилам на основании выборочных данных, называется наблюдаемым значением критерия (Кнабл). Вся числовая ось ожидаемых значений статистики включает область допустимых величин и критическую область (или области). Их отделяют друг от

75

друга критические точки (Ккрит ), которые определяются на за-

данном уровне значимости α по таблицам распределения случайной величины К, выбранной в качестве критерия.

Основная методика проверки статистических гипотез заключается в следующем:

– если наблюдаемое значение критерия (Кнабл ) принадлежит критической области, нулевая гипотеза Н0 отклоняется

впользу конкурирующей;

–если наблюдаемое значение критерия (Кнабл ) принадле-

жит области допустимых значений, нулевую гипотезу H0 нельзя отклонить (рис. 3.1, 3.2), следовательно, она принимается.

Можно принять решение относительно нулевой гипотезы H0 путем сравнения наблюдаемого (Кнабл ) и критического значения критерия (Ккрит ).

При правосторонней альтернативной гипотезе:

– если Кнабл < К2крит , нулевую гипотезу H0 нельзя откло-

нить;

– если Кнабл > К2крит , нулевая гипотеза H0 отклоняется, принимается альтернативная Н1 .

При левосторонней конкурирующей гипотезе:

– если Кнабл > К1крит , нулевую гипотезу H0 нельзя откло-

нить;

– если Кнабл < К1крит , нулевая гипотеза H0 отклоняется в пользу конкурирующей Н1 .

При двусторонней конкурирующей гипотезе:

–если К1крит < Кнабл < К2крит , нулевую гипотезу H0 нельзя отклонить;

–если Кнабл > К2крит или Кнабл < К1крит , нулевая гипоте-

за H0 отклоняется, принимается альтернативная Н1 .

76

Проверка статистических гипотез выполняется в такой последовательности:

1)сформироватьнулевуюH0 иальтернативную Н1 гипотезы

иустановитьнеобходимыйидостаточныйуровеньзначимости;

2)из рекомендованных критериев для проверки статистических гипотез выбрать наиболее подходящий (например, по табл. 3.3), точное или приближенное распределение которого заранее известно;

3)в статистической программе или по таблицам распределения случайной величины К, выбранной в качестве статистического критерия, найти критическое значение К (критическую точку или точки);

4)на основании выборочных данных по принятым мето-

дикам вычислить наблюдаемое значение критерия Кнабл ; 5) по виду конкурирующей гипотезы Н1 определить тип

критической области; 6) определить, в какую область (допустимых значений или

критическую) попадает наблюдаемое значение критерия Кнабл, и

в зависимости от этого принять решение относительно нулевой гипотезы H0 [1].

3.3.4. Число степеней свободы

За редкими исключениями расчетное выражение эмпирических функций распределения, например Fэмп, включает количество наблюдений в исследуемой выборке, его часто обозначают как n. В этом случае эмпирическое значение критерия может становиться тестом для проверки статистических гипотез. По специальным таблицам или расчётами мы определяем, какому уровню статистической значимости различий соответствует данная эмпирическая величина.

77

Когда имеются выборки, разные по количеству данных, одно и то же эмпирическое значение критерия может оказаться как значимым, так и незначимым. Значимость будет связана с количеством наблюдений в исследуемой выборке n. Понятно, чем больше наблюдений в выборке, тем больше степень доверия к статистическим выводам по этой выборке. От количества наблюдений зависит так называемое число степеней свободы, которое обозначается как или df. Количество степеней свободы равно числу классов вариационного ряда минус число условий, при которых он был сформирован [1]. Например, в группе 25 студентов закончили сессию с положительными оценками (на 3, 4 и 5). Студенты сгруппированы в три класса по оценкам 3, 4, 5, вектор положительных оценок равен 3. Из группы 8 студентов имеют отличные результаты по сессии, 11 с хорошими оценками. Следовательно, число троечников можно вычислить как остаток 25 – (8 + 11) = 6. Если можно вычислить число студентов третьей группы, то она «не свободна». В примере «свободны» только две группы с оценками 4 и 5.

Число степеней свободы равно числу классов вариационного ряда минус число условий, при которых он был сформирован. К числу таких условий при проверке выборки на нормальность её распределения относятся объем выборки n, средние и дисперсии. Для рассмотренного примера число степеней свободы рассчитывается так:

где r – общее количество интервалов разбиения; с – количество «несвободных интервалов».

Варианты более сложного расчета числа степеней свободы будут приведены в разделах, посвященных критерию χ2 и дисперсионному анализу. Зная n (или число степеней свободы ), по специальным таблицам мы можем определить критические значения критерия и сопоставить с ними полученное эмпирическое

78

значение. Обычно это записывается так: «при n = 25 критические значения критерия составляют…» или «при = 2 критические значения критерия составляют…».

3.3.5. Статистическая значимость. Р-уровень значимости

Ранее мы показали вероятностный характер происхождения наших данных (мы считаем, что они получены путем случайного выбора) (пп. 1.4, 2.2, 2.5). Поэтому все дальнейшие суждения, основанные на этих данных, будут также иметь вероятностный характер.

Висследованиях представленных наблюдений мы не застрахованы от ошибок. Такие ошибки считаются допустимыми, если они не превышают априори заданные значения. Например, на руднике отобраны 200 проб, по две из каждой борозды. Причём 100 проб отправили в первую лабораторию, а дублирующие 100 проб отправили во вторую лабораторию [46]. После выполнения химических анализов получили расхождения в содержании полезного компонента, из которых 96 проб имеют расхождение меньше 1 %, а 4 пробы получились с расхождением, больше априори заданного 1 %. Требуется определить, существенно ли статистически такое отклонение или нет. Повышенное расхождение в пробах имеет место не чаще, чем в четырёх случаях из ста. Такое утверждение соответствует расчётной (эмпирической) вероятности ошибки рэмп = 4 : 100 = 0,04.

Вэтом примере pэмп – расчётный уровень значимости, или вероятность того, что расхождение в пробах носит случайный характер, а не является свойством генеральной совокупности.

Какова вероятность получить в следующих пробах, отобранных в аналогичных условиях и обработанных в этих же лабораториях по ранее использованным методикам, расхождение в парных пробах больше допустимого значения? В статистике та-

79

кая вероятность рассчитывается и именуется p-уровнем значимости (p-value, p-значение). Эта статистика состоит в обратной зависимости от истинности результатов. Низкое значение р-уровня соответствует высокой степени доверия к результатам исследований, а большое значение вероятности будет свидетельствовать о низком доверии к результатам работы лабораторий. В последнем случае, если корректность работы лабораторий не вызывает вопросов, тогда расхождение в пробах носит не случайный характер, а является свойством генеральной совокупности.

3.3.6. Критический уровень значимости ошибки принятия гипотез

Итак, рассчитанный p-уровень рассматривается в качестве статистики, отражающей уровень вероятности ожидаемых ошибок. Какую вероятность следует считать малой при принятии той или иной гипотезы? Отвечая на данный вопрос, необходимо учитывать степень опасности совершения ошибки. Обычно вероятность ошибочного вывода тем меньше, чем больше объём наблюдений. Если в исследованиях используются малые по объёму выборки, то в этих случаях вероятность ошибки может быть значительной.

В качестве «допустимой границы» уровня ошибок принимается критическое значение вероятности. Эта граница и называется «уровнем значимости» (критическим, или табличным) и обозначается греческой буквой . Она задается заранее малым числом, чаще всего используют некоторые стандартные значе-

ния: 0,05; 0,01; 0,005; 0,001. В программе Statistica в статистиче-

ском калькуляторе критические значения можно рассчитать для любых условий [10; 66].

Например, считаем допустимым в 100 парных пробах 5 отклонений с разностью содержания полезного компонента

80