книги / Прикладной статистический анализ в горном деле (Одномерная математическая статистика и регрессионный анализ)

Прежде всего преобразуем выборку в вариационный ряд, упорядочив наблюдения в порядке возрастания. В результате получим: 1 2 3 4 5 6 7 9 10 10 11 11 12 12 13 13 14 14 15 16 17 18 28. Легко заметить, что последнее число в вариационном ряду 28 представляет собой резко выделяющееся на фоне остальных наблюдение, его можно считать грубым наблюдением, или выбросом. Рассмотрим, насколько различные статистические характеристики чувствительны к рассматриваемому выбросу. Результаты расчетов представленывтабл.2.5.

Таблица 2.5

Результаты вычисления статистик при наличии и отсутствии грубого наблюдения

Из приведенной таблицы видно, что при удалении одной пробы (выброса) изменились среднее и стандарт (сигма). А значения медианы, квартилей и межквартильного расстояния остались прежними. Этот пример дает наглядную иллюстрацию преимущества непараметрического подхода, основанного на медиане и квартилях. Заметим, что можно пользоваться и традиционными оценками среднего и дисперсии при наличии четко определенной процедуры выявления резко выделяющихся наблюдений. Такая процедура описана в п. 2.11.2.

51

2.10. Показатели качества

Особую группу статистик образуют показатели, характеризующие качество и надежность технологического процесса. Рассмотрим эти показатели на примере отработки Верхнекамского месторождения калийных солей.

К основным показателям качества на ВКМКС можно отнести коэффициенты запаса точности Cpk и Cp, а также коэффициент засоренности g.

2.10.1. Коэффициент запаса точности Cpk

Количественной характеристикой степени соответствия технологического процесса требованиям технических условий (ТУ) является так называемый коэффициент запаса точности Cpk который определяется следующей формулой:

где Xср – характеристика среднего, SL – ближайшая к среднему граница поля допуска на параметр (сокращение от английского Specification Level – «граница допуска»), σ – стандартное отклонение.

В качестве оценки σ используют выборочное стандартное отклонение s. Таким образом, коэффициент Cpk определяется отношением расстояния от среднего до браковочной границы к естественному статистическому разбросу, который принято считать трехсигмовым. В приведенной формуле предполагается, что среднее значение X лежит внутри поля допустимых значений, определяемого требованиями документов. В противном случае считают, что Cpk равен нулю.

Перед обогащением на рудном складе отбираются пробы. Каждая проба сильвинита разделена на две части. По результатам анализов среднее содержание химических компонентов

52

хлорида калия в пробах составило 34,66 %, оценка стандарта s =0,48%.Кондиционное(минимальное)содержаниеKCl = 26,0 %, верхняя граница кондиций отсутствует.

Тогда Cpk = |34,66 – 26,00| / (3·0,48) = 2,00. Согласно при-

нятой практике считается, что если Cpk < 1, то технологический процесс обогащения не может считаться удовлетворительным и требует большого расхода реагентов. Если Cpk находится в пределах от 1 до 1,33, то процесс может быть использован для опытного и мелкосерийного производства. Процесс будет надёжным, если для него Cpk ≥ 2. Мониторинг коэффициента Cpk позволяет отследить динамику (тренд) процесса во времени или пространстве.

В приведённом примере коэффициент запаса точности равен 2,00. Это свидетельствует о стабильном содержании хлористого калия на складе, среднее содержание выше кондиционного значения.

Если пласт на каком-либо участке имеет сложную гипсометрию, то в процессе добычи будут подрублены вмещающие породы. В этом случае качество извлечённой руды будет ниже среднего значения, определённого в пробах, и может быть даже ниже установленных кондиций по качеству на добычу. Для повышения качества рудной массы на складе потребуется примешивание к ней руды с богатым содержанием.

2.10.2. Потенциальный коэффициент запаса точности Cp

Наряду с коэффициентом Cpk часто рассматривают еще один вспомогательный показатель Cp, который может быть назван потенциальным коэффициентом запаса точности Cp. Он определяется по формуле

53

где USL и LSL – соответственно верхняя и нижняя границы поля допуска, σ – стандартное (среднеквадратичное) отклонение. Нетрудно заметить, что коэффициенты Cpk и Cp совпадают, если среднее значение находится точно посередине поля допуска. Если же среднее значение сдвинуто относительно середины поля допуска, то Cpk < Cp. Таким образом, Cp определяет потенциальный (максимально возможный) запас точности в то время как Cpk определяет реально имеющийся запас точности. Если Cpk оказывается существенно ниже, чем Cp, то принимают решение о регулировании процесса (предполагается, что номинал совпадает с серединой поля допуска). Нередко поле допуска имеет только одну естественную границу, как это показано в предыдущем примере. В этом случае рассчитывают только Cpk, расчет Cp не имеет смысла. Коэффициенты Cpk и Cp часто называют также коэффициентами стабильности и воспроизводимости.

2.10.3. Коэффициент засоренности данных g

Одним из наиболее важных параметров, характеризующих качество технологического процесса и измерений, является степень засоренности данных g, равная количеству резко выделяющихся наблюдений в процентах:

где k – количество резко выделяющихся наблюдений (выбросов), n – полное число наблюдений (объем выборки). Методика выявления резко выделяющихся наблюдений описывается ниже в п. 2.11.2. Для пластов ВКМКС этот коэффициент показывает степень неравномерности распределения полезного компонента на участке пласта.

54

2.11. Теоретические функции распределения

2.11.1. Общие сведения

Если мы выстроим ряд из 10 чисел от 0 до 9, то в нём каждая цифра встречается только один раз. Построим график зависимости частоты упоминаний каждого числа в этой выборке от его порядкового номера, на графике получим прямую линию, параллельную оси абсцисс. Частота появления цифр в указанном интервале одинакова, каждая цифра встречается один раз, поэтому на графике получаем прямую линию, что свидетельствует о равномерном законе распределения этого ряда (как на рис. 2.3). При наблюдении реальных случайных величин в природе, технике, социологии и других областях наблюдаемые величины не будут встречаться с одинаковой частотой. В предыдущих разделах показано, что случайная величина, сгруппированная по интервалам, принимает значения от минимального до максимального с неодинаковой частотой. Для описания частоты появления проб с заданным содержанием полезного компонента и соответствия между всеми возможными их значениями и частотами была рассмотрена эмпирическая функция распределения (п. 2.4). Эта функция, вычисленная по выборке из генеральной совокупности, позволяет нам предсказать вероятность попадания случайной величины в априори заданный интервал при следующем испытании. В общем случае для генеральных совокупностей различных случайных величин можно представить себе бесконечное разнообразие законов распределения.

Ранее указывалось, что теоретические исследования различных процессов и явлений позволили доказать, что на самом деле существует и используется небольшой набор теоретических законов распределения (нормальное, показательное, равномерное и некоторые другие), которые чаще всего встречаются в природе [12], технике, геологии и горном деле, в социологии и

55

других областях. Это связано с тем, что различные случайные величины могут иметь совершенно одинаковые теоретические законы распределения. Очень часто случайные величины имеют подобные законы распределения, например, р (х) для них выражается формулами одинакового вида, отличающимися только одной или несколькими постоянными. Эти постоянные называются параметрами распределения. В теории вероятностей используются самые разные законы распределения, в дальнейшем рассмотрим несколько наиболее типичных из них. Важно обратить внимание на условия, в которых они возникают, на параметры и свойства этих распределений.

Различие между теоретической и эмпирической функциями распределения состоит в том, что теоретическая функция распределения Fтеор (x) определяет вероятность события Х < x для генеральной совокупности, а эмпирическая функция распределения Fэмп (x) определяет относительную частоту этого же события для выборки [20].

При статистическом исследовании выборки нас обычно интересует вопрос, насколько точно экспериментально полученное распределение случайной величины (значения переменной) можно аппроксимировать тем или иным теоретическим распределением. Как уже отмечалось, для описания реальных явлений исследователями используются различные теоретические распределения: нормальное, Стьюдента, хи-квадрат, Фишера, биномиальное, отрицательное биномиальное и др. Рассмотрим более подробно методику проверки соответствия нормальному закону распределения значений переменных.

2.11.2. Нормальный закон распределения

Нормальное распределение в горном деле важно по многим причинам. В большинстве случаев оно является хорошим приближением погрешностей, например, геодезических и маркшей-

56

дерских измерений. Распределение многих статистик является нормальным или может быть получено из других с помощью некоторых преобразований.

Главной особенностью нормального распределения является то, что оно представляет собою предельный закон, к которому приближаются другие законы распределения при выполнении определенных условий. По мнению научного директора компании StatSoft Russia, изложенному в электронном учебнике по статистике [70], нормальное распределение представляет собой одну из эмпирически проверенных истин общей природы действительности и его положение может рассматриваться как один из фундаментальных законов природы.

Нормальным распределением хорошо описываются экспериментальные наблюдения:

–у которых имеется тенденция группироваться вокруг

центра;

–положительные и отрицательные отклонения от центра равновероятны;

–малые по абсолютной величине значения встречаются чаще больших.

Нормальная кривая обладает следующими особенностями. Она похожа на колокол (рис. 2.1). Её левая и правая ветви спадают одинаково в обе стороны сначала медленно, а потом быстро. Специалисту достаточно знать три параметра, чтобы построить эту кривую: высоту её максимума, среднее значение изучаемой величины (это и есть то место на горизонтальной оси, которое соответствует вершине горба кривой) и ширину кривой. Условно ширину кривой измеряют на половине высоты колокола. Понятно, что ширина показывает, насколько часто или редко встречается отклонение от среднего. Чем уже колокол, тем меньше отклонения от среднего значения.

Функция распределения нормальной случайной величины X

обозначаетсяF (x, x , 2 )изадаётсясоотношением

57

где x –среднеезначение; 2 –дисперсия; x –значениевеличины. Из выражения (2.22) следует, что нормальное распределение описывается двумя параметрами – средним значением (x ) и

стандартным отклонением (σ).

В практике статистических исследований могут встречаться данные, различные по размеру, например, содержание в пробе нерастворимого остатка (NО) равно 0,1 %, а высотная отметка выработки Н, где отобрана проба, равна – 450,25 м. При сравнении статистических оценок, к примеру стандарта нерастворимого остатка и отметки пробы, различие дисперсий будет очень большим. Чтобы избежать большого различия в данных, их нормируют по стандарту в отклонениях от среднего:

Такая переменная называется нормированной. В программе Statistica она именуется стандартизированной. Характерной чертой нормированной переменной является равенство нулю среднего значения и равенство единице дисперсии. Такой ряд называют нормированным с нулевым средним и единичной дисперсией.

Нормальный закон с параметрами x = 0 и 2 = 1 называется стандартным, он описывается функцией Лапласа:

Характерное свойство нормального распределения состоит в том, что 68 % всех его наблюдений лежат в диапазоне среднее

± 1 стандартное отклонение, а в диапазоне среднее ± 2 стандартных отклонения уже содержит 95 % значений. Другими словами,

58

при нормальном распределении стандартизованные наблюдения с нулевым средним и единичной дисперсией, меньшие – 2 или большие + 2, имеют относительную частоту менее 5 % [20].

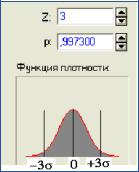
Графически нормальное распределение характеризуется «колоколообразной кривой», симметричной относительно среднего значения (рис. 2.2). На рисунке видно, что внутри интервала ± 3σ находятся 99,73 значений.

Рис. 2.2. Функция плотности нормального распределения для условий: x ± (3 σ) при = 1, x = 0

Среднее, мода и медиана на графике рис. 2.2 совпадают. При увеличении дисперсии график становится пологим, приближаясь к оси абсцисс. Уменьшение дисперсии делает график плотности вероятности вытянутым вверх.

В маркшейдерском деле и геодезии для оценки качества наблюдений и выявления грубых ошибок используются величины стандартных отклонений, равных 2 и 3 .

Площадь под графиком нормальной плотности (для нормированных данных), лежащая в интервале от – 3σ до + 3σ, составляет 99,73 % всей площади. Из тысячи наблюдений только 3 (а точнее 2,7) наблюдения могут быть за границей этого интервала. На границе графика находятся большие по абсолютной величине значения. Таким образом, знание среднего значения случайной величины и ширины кривой нормального распреде-

59

ления позволяет уверенно определить грубые наблюдения и отделить возможные события от невозможных.

Если исследуются ряды измерений малого объёма, например, ошибки измерения горизонтальных углов теодолитных ходов, где количество пунктов ограничено нормативными документами до 20–25, то можно использовать двухсигмовый интервал (от – 2σ до + 2σ). При этом площадь под графиком нормальной плотности составляет 95,45 %, из 25 погрешностей наблюдений только одна, возможно, будет грубой (а точнее 1,14 наблюдения).

Для ответа на вопрос, подчиняется ли выборка значений переменной (случайных переменных) нормальному закону распределения, применяют:

–визуальные методы соответствия (например, анализ гистограмм и нормальных вероятностных графиков);

–численные методы проверки числовых значений параметров распределения (асимметрии, эксцесса, наличие выбросов);

–проверка гипотез о нормальном распределении по критериям согласия (χ2, Колмогорова и др.).

2.11.3. Равномерное распределение

Непрерывная случайная величина X равномерно распределена на отрезке [a, b], «если на этом отрезке плотность распределения случайной величины постоянна, а за границами отрезка плотность равна нулю» [38].

где 1 / (b – a) = const.

Графики плотности f (x) и функции F (x) равномерного распределения представлены на рис. 2.3.

60