книги / Методы измерений в волоконной оптике

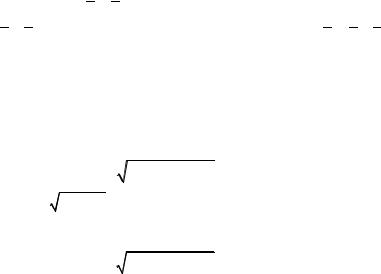
Чтобы оценить погрешности, достаточно определить их предельные значения, для чего необходимо учесть наибольшие и наименьшие значения, которые может принять функция q. Максимальное значение функции q: qmax = x + y + (∆ x + ∆y) . Минимальное значение функции q:

= x + y − (∆ x + ∆y) . Наилучшая оценка для q: q = x + y . Погрешность для функции q: ∆q ≈ (∆ x + ∆y) .

Полученное выражение переоценивает величину погрешности. Если измерения х и у выполнены независимо и если результаты замеров обеих величин подчиняются нормальному распределению, то погреш-

Докажем квадратичное сложение погрешностей функции q = x + y. Для упрощения предположим, что истинные значения величин х и у та-

ковы: х = 0 и y = 0.

Тогда

P(x) ~ е− x22σ2x = exp{− x2 2σ2x}, P( y) ~ е− y2 2σ2y = exp{− y2 2σ2y } .

Поскольку х и у измерялись независимо, вероятность получения любых данных х и у равна произведению вероятностей:

Выразим теперь показатель экспоненты через переменную (х + у). Для этого воспользуемся следующим тождеством (справедливость которого можно проверить простыми преобразованиями правой части):

101

Применим это тождество к формуле для вероятности Р(х,у):

Но нам нужно выражение Р(х + у), не зависящее от какого-либо значения z. Чтобы избавиться от z, проинтегрируем P(x+y, z) по всем возможным значениям переменной z:

С полученным интегралом мы уже ранее встречались, его значение

равно константе и не учитывается в наших оценочных расчетах. Тогда

Таким образом, значения функции q = x + y распределены нормально с центром в Х = 0, Y = 0 и с шириной σq = σ2x + σ2y .

В общем случае необходимо принять во внимание как случайные, так и систематические погрешности. При этом стандартная погрешность измеряемой величины х рассчитывается по формуле

∆ x = (∆ x)сист2 + (∆ x)случ2 .

Основы корреляционного и регрессионного анализа

В функциональной связи Y = f (X) каждому значению независимой

переменной X отвечает одно вполне определенное значение зависимой переменной Y. Если независимой переменной соответствует несколько значений Y, то связь между переменными X и Y приобретает статистический характер и называется корреляционной.

Простейшей и распространенной зависимостью между величинами

X и Y является линейная регрессия. Оценка тесноты или силы связи

между величинами X и Y осуществляется методами корреляционного анализа.

102

Рассмотрим линейную регрессию от одного параметра (рис. 4.8). Пусть для произвольного фиксированного значения x получено несколько значений Y. Предполагается, что величина Y распределена нормально с математическим ожиданием

Рис. 4.8. Корреляционное поле зависимости Y = f (х) с эмпирической (1) и теоретической (2) линиями регрессии

и дисперсией σ2y , не зависящей от X. Примем, что случайная величина Y

всреднем линейно зависит от фиксированного значения x, а параметры k, b и σ2y являются неизвестными параметрами генеральной совокупности.

Для оценки этих неизвестных величин по выборке объемом n сопряженных пар значений x1, y1; x2, y2; …; xn, yn в декартовой системе координат можно построить корреляционное поле, содержащее n точек. Если нанести на поле средние значения yi , соответствующие всем зна-

чениям переменной xi, то зависимость y от x станет более очевидной. Ломаная линия, соединяющая точки yi , отнесенные к серединам

интервалов xсрi, называется эмпирической линией регрессии. С увеличением числа измерений ломаная линия сглаживается и приближается к предельной линии – теоретической линии регрессии.

Метод наименьших квадратов

Для линейной зависимости линия регрессии задается уравнением прямой

103

неизвестные коэффициенты которой определяются по методу наименьших квадратов. В соответствии с этим методом квадрат расстояния по вертикали между опытными точками с координатами xi, yi и соответствующими точками на линии регрессии должен быть минимальным:

откуда

Пример. Построить линейную зависимость регрессии по семи экспериментальным точкам:

104

Решение

По формуле (4.48) получаем искомую зависимость y = y + k ( x − x ) = 2, 764 + 0,157 ( x − 4 )

Выборочный коэффициент корреляции

Коэффициент корреляции является количественной мерой, учиты-

где σx и σy – стандартные отклонения.

Коэффициент корреляции не может быть использован для оценки важности фактора. Его величина указывает только на тесноту связи между переменными, а знак – на характер влияния. Значения коэффициента корреляции находятся в пределах −1≤ r ≤ 1:

при r < 0 – увеличение x вызывает уменьшение y; при r > 0 – увеличение x вызывает увеличение y;

при | r | = 1 – связь между x и y линейная функциональная;

при | r | = 0 – корреляционной связи между x и y нет или она нелинейная.

Если выражение (4.45) преобразовать к виду

i=1

105

и подставить в формулу (4.47), то получим

Отсюда видна непосредственная связь коэффициента корреляции r и коэффициента k в уравнении линейной регрессии, их знаки всегда совпадают.

Выражения (4.49), (4.51) выражают тесноту и вид связи между переменными x и y.

4.4.Вопросы для самоконтроля

1.Какова связь и различия между фундаментальными научными понятиями «физическая величина» и «информация»?

2.Истинное и действительное значения физической величины, абсолютная и относительная погрешности измерений.

3.Перечислите различия между измерением и контролем.

4.Тестирование, достоверность и погрешность тестирования.

5.Отличие протокола от счета, измерения и тестирования.

6.Что включает в себя контроль, чем обеспечивается единство контроля?

7.Отличия между дискретизацией, квантованием и числовым кодированием оптического сигнала.

8.Виды контроля: прямой, косвенный, допусковый, односторонний, многосторонний, активный, пассивный, локальный, дистанционный. Приведите примеры.

9.Видыизмерений: прямые, косвенные, статические, динамические.

10.Модификации метода сравнения с мерой.

11.Типы погрешностей измерения.

12.Расчетсистематическихпогрешностей, классыточностиприборов.

13.Закономерности распределения случайных погрешностей, функция нормального распределения, стандартное отклонение.

14.Надежность ограниченной серии измерений, распределение Стьюдента.

15.Статистический принцип максимального правдоподобия. Корреляционная функция, коэффициент корреляции, его смысл.

16.Метод наименьших квадратов для определения линейной рег-

рессии.

106

5. МЕТОДЫ ИЗМЕРЕНИЙ В ВОЛОКОННОЙ ОПТИКЕ

5.1.Измерения параметров оптического волокна

Вобщем случае весь спектр измерений в волоконно-оптических системах передачи можно разделить на два основных типа: это системные и эксплуатационные измерения. Первые заключаются, например,

вопределении целостности волокна при помощи оптического рефлектометра, а вторые – в определении функционирования системы с позиций параметров передачи, примерами которого являются измерение потерь, измерение дисперсии и измерение ширины линии лазера. Для обеспечения работоспособности и соответствия проектным параметрам волоконно-оптических систем передачи необходимо проводить множе-

ство как системных, так и эксплуатационных измерений, которые, в свою очередь, отличаются методикой и используемыми средствами измерений. Рассмотрим основные виды измерений параметров оптического волокна (рис. 5.1).

Рис. 5.1. Основные виды измерений параметров оптического волокна

Измерения в зависимости от типа волокна включают измерение затухания, межмодовой и хроматической дисперсии, цифровой апертуры, диаметра сердцевины, длины волны отсечки и размера модового пятна.

107

Наиболее важным параметром оптических волокон является затухание, измерение которого осложняется распространением большого количества мод в данном волокне, каждая из которых имеет свои собственные характеристики распространения. Для тестирования ослабления волокно должно быть возбуждено в режиме равновесного распределения мод (EMD), представляющем собой распределение мод для достаточно большой длины волокна, а измерение должно быть проведено путем сравнения вносимых потерь короткого эталонного волокна с потерями всего тестируемого волокна. Для этой цели могут использоваться источник и измеритель оптической мощности, а при необходимости получения дополнительной информации о равномерности ослабления на всей протяженности волокна необходимо проводить анализ обратнорассеянного сигнала при помощи оптического рефлектометра.

Межмодовая дисперсия – это технический термин для обозначения расширения импульса (сужения полосы пропускания) вследствие неравных скоростей распространения различных мод. Основная концепция измерения межмодовой дисперсии заключается в возбуждении волокна коротким EMD-импульсом с последующим измерением ширины импульса на конце волокна. При этом для измерения должен быть использован источник с узкой шириной спектра, например, как у лазерного диода.

Хроматическая дисперсия – это расширение импульса вследствие отличия скоростей различных длин волн, содержащихся в спектре источника, которое отражает свойство материала волокна. Поэтому при хроматической дисперсии расширение импульса непосредственно зависит от ширины спектра источника. Так как хроматическая дисперсия не может быть непосредственно измерена, для ее определения необходимо к результату измерения добавить значение межмодовой дисперсии.

Числовая апертура (NA) и диаметр сердцевины определяют то значение мощности, которое можно ввести в многомодовое волокно. Числовая апертура определяет максимальный угол направленных лучей в волокне и всегда измеряется на выходе волокна. При этом предполагается, что максимальный угол, наблюдаемый на выходе, приблизительно равен максимальному углу на входе, а в волокно введены все моды.

Диаметр сердцевины измеряется на выходном конце волокна путем измерения распределения мощности при полном возбуждении на входе.

Длина волны отсечки одномодового волокна определяет самую низкую длину волны, которую следует использовать, если особую важность имеет высокая полоса пропускания, зависящая только от хрома-

108

тической дисперсии, поэтому для ее определения влияние межмодовой дисперсии можно не принимать в расчет. Основная идея измерения полосы пропускания заключается в измерении импульсной характеристики волокна путем сравнения импульсов на его входе и выходе, а также в измерении амплитуды выходного сигнала при возбуждении волокна модулированным переменной частотой гармоническим сигналом.

Ниже длины волны отсечки будет распространяться большее количество мод. Поэтому длина волны отсечки измеряется вводом в короткое волокно широкого спектра излучения, например, от вольфрамовой лампы, а затем осуществляется измерение ослабления каждой спектральной составляющей. Длина волны отсечки в этом случае определяется как отсутствие непрерывности кривой ослабления, ибо наличие большего количества мод позволяет большему объему возбужденной мощности достичь конца волокна. Другой метод измерения основан на условии, что моды высокого порядка более чувствительны к изгибам волокна, чем фундаментальные моды. Для проведения этих измерений источник должен обеспечивать стабильность интенсивности излучения

ипостоянство длины волны, согласованной со спектральной чувствительностью детектора.

Диаметр модового пятна характеризует расстояние между двумя точками, в которых измеренная мощность составляет 1/е от максимальной мощности при условии аппроксимации излучения фундаментальной моды одномодового волокна лучом с распределением Гаусса как внутри него, так и снаружи. Особенностью луча Гаусса является то, что он полностью определяется только двумя показателями: радиусом точки

идлиной волны. Поэтому характеристики излучения, в частности поле на выходе волокна, могут быть определены исходя из этих показателей.

Если длина волны измерения больше длины волны отсечки одномодового волокна, в нем будет распространяться только одна мода. При таком условии измерения ослабления одномодового волокна значительно проще, чем аналогичные измерения многомодовых волокон,

исогласно методу обрыва выполняются в два этапа: сначала измеряется выходная мощность на удаленном конце волокна с повторным измерением на части отрезанного у входного конца волокна. Разность уровней мощности, выраженная в оптических дБ, и является ослаблением. При необходимости получения дополнительной информации о равномерности ослабления на всей протяженности волокна необходимо проводить анализ обратнорассеянного сигнала при помощи оптического рефлектометра.

109

5.2. Методы определения размеров волокна

Стандарт регламентирует практическое измерение длины и размеров поперечного сечения оптического волокна. Размеры оптических волокон определяют путем проведения испытаний образцов в соответствии с табл. 5.1, в которую включены все категории волокон, но не все виды испытаний для данной категории волокон.

1.Метод ближнего поля непосредственно реализует определение сердцевины через профиль показателя преломления. Данный метод позволяет получить профиль показателя преломления, по которому могут быть определены размеры и числовая апертура.

2.С помощью распределения света в ближнем поле получаемые размеры связаны с профилем показателя преломления, но не имеют точного соответствия определению диаметра сердцевины.

3.Метод четырех концентрических кругов является контрольным испытанием, обычно основанным на распределении света в ближнем поле. Он не может использоваться для измерения действительных значений размеров волокна.

4.Для практических целей диаметр сердцевины одномодовых волокон, как правило, не нормируется.

110