Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Пермский национальный исследовательский политехнический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

книги / Теория химических реакторов введение в основной курс

..pdf

Скачиваний:

Добавлен:

12.11.2023

Размер:

5.34 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 2223 / 2423 24 > Следующая >>>

τ	τ	f d	1	F p .	(7)
			n
0	0		p

При такой форме записи дифференциального уравнения на комплексное число р распространяются обычные правила обращения с алгебраическими сомножителями, т.е. его можно выносить за скобки, сокращать и т.д.

Техника прямого и обратного преобразования Лапласа

Основные свойства преобразования Лапласа:

1.	Однородность: если f τ F p , тоλf (τ) λF p .
2.	Аддитивность: если f τ F p и τ φ p , то

f τ τ F p φ p .

	Подобие: если f ( ) F( p) , то f ατ		1		p
3.			α	F		.

					α
4.	Правило дифференцирования оригинала (см. (5), (6)).
5.	Дифференцирование изображения:	если f τ F р ,
то τf	τ F р . Обобщение: 1 n τn f τ F n p .
6.	Интегрирование изображения: если		f τ F p , то

fτ F z d z , где z – произвольная комплексная переменная.

τp

7.Правило сдвига (теорема запаздывания): если f τ F p ,

то f τ t e pt F p .

8. Правило затухания (теорема смещения): если f τ F p ,

то eλτ f τ F p λ .
Существуют ограничения:	Re p S0 Re λ;	f τ	MeS0τ;
Существуют ограничения:	Re p S0 Re λ;	f τ	MeS0τ;
M 0; S0 – показатель роста, S0	0.

220

9. Теорема свертывания (умножения изображений). Сверткой функции f τ и τ называется функция от τ,

определяемая равенством ( ) f (u) (t u)du и обозначае-

мая f , читается: функция f(τ) свернута с функцией φ(τ).
Свойства свертки:
– коммутативность: f f ;
– ассоциативность: f f		;
– рефлексивность: f f		.
Если f F p и p , то f F p p .
10. Формула Дюамеля: если lim f f 0			и f F p ,
	0

а p , то p F( p) ( p) f (0) ( )
а p , то p F( p) ( p) f (0) ( )			f (u) ( u)du.
	f F p и f	0		p
11. Если	f F p и f	– оригинал,	то lim pF	p
			p
lim f .
0	lim f существует, то lim pF p lim f .
12. Если	lim f существует, то lim pF p lim f .
		p 0

Кроме этого, существует две теоремы разложения дробей, которые описаны в соответствующих руководствах.

Примеры:

1. Вычислить изображение единичной функции Хевисайда:

	0 при < 0,
	( )			> 0.
	1 при			> 0.
						1
	Поскольку F p e p 1d						e p


						p
				0	0	p
1	, то	1	.
p		p

221

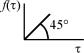
2. Вычислить изображение функции f .

	F p																					1
				e p d													e p						e p d


					0										p					0		p	0
					0										p					0		p	0
			e p								1		e p
											1
										p2
		p
		p											0
(интегрирование по частям: u = τ du = dτ, dv e p d																																			v			1		e p ) =
(интегрирование по частям: u = τ du = dτ, dv e p d																																			v			p		e p ) =
																																						p
	p				1																			0				1
e	p				1																			0				1
													lim								1										.
		p				p	2				0		lim					pe	p		1			p			p			2	.
		p				p					0							pe						p			p
																																				1
Поскольку по правилу Лопиталя lim																																lim									0	,
Поскольку по правилу Лопиталя lim																										pe		p				lim				2	e	p			0	,
																										pe										p	e

получаем									1			.
получаем												.
								p2
	3. Вычислить изображение функции																											f ea :

	F p				e p ea d e(a p) d e ( p a)																															1			.
																																				1

							0											0												p a				0		p a
							0											0												p a				0		p a
	Следовательно, ea																	1			.
	Следовательно, ea																	p a			.
																		p a
	4. Вычислить изображение																				f	cos .
	Представим косинус в комплексном виде (формула Эйлера):
														cos							ei e i
														cos								2			.
																						2
	По правилу аддитивности, учитывая пример 3, получим
														1				1				1									1
											cos			1				1				1									1		.
											cos			2								p i							p		2		.
														2		p i						p i							p			1

222

5. f ea 1 . По правилу аддитивности, учитывая при-

меры 1 и 3:
e	a	1		1		a
		1					.
		1	p a		p	p p a	.

6. f cos αt. По правилу подобия, с учетом примера 4:

cos

p 2

p2 2

7. Найтиизображениеcos

, если sin

; sin 0 0,

p2 2

cos 1 sin . Используем правило дифференцирования оригинала(5):

			df			pF p pf 0 ,
			d
				1																					p
cos				1		p										0									p				.
cos						p			p		2	2				0					p			2				2	.
									p												p
																			f									2
8. f 1 d ;				f							d ;								f									2		. Используем
0											0														0			2
формулу (7), учитывая примеры 1, 2.
												1					1			1
												1					1			1
	1 d																							,
	1 d								1			p					p			p		2		,
	0								1			p					p			p
										2			1					1				1
										2
d																										,
d							1 2							p				2				3				,
0							1 2							p				p					p
		2						3						1				1					1
														1				1					1				.
0 2					1 2 3													p3									.
0 2					1 2 3										p			p3					p4
																														223

Отсюда

pn 1

9. Интегрирование изображения (правило 6):

ea eb

d z

z a

ln z a ln z b

z a

z b

limln

z a

p a

ln1 ln

p a

p b

z b

p a

10. Интегрирование изображения (правило 6) с учетом примера 7 при α = 1:

sin		1
	p		dz arctg z			arctg	p arcctg p.

		z2 1		p	2

11.f t (применяется правило 7):

t 1p 1p e pt 1 pe pt .

12.f e sin (применяется правило 8):

sin		(пример 7), отсюда e sin					.

	p2 2			p 2		2
	p2 2			p 2		2
Для косинуса (см. пример 7): e cos			p		.
Для косинуса (см. пример 7): e cos			p 2 2		.
			p 2 2
13. f	ch cos (правило 8):

ch 12 e e f cos 12 e e

12 e cos 12 e cos .

Далее – см. пример 12.

224

14. Найти свертку

f sin

и et .

u e

-u

sin

f sin u e du e

sin u

d e u du

d cos udu

e u

-u

sin u

cos u du

u e-u

u e u

e sin

cos

cosu

d e u d

d sin u

du e u

u e

cos u e

sin

u du

= sin u e u cosu e u

sin u e udu

2 sin u e u du sin

исходный

u e u

cos u e u

sin u e u du 1

sin

u e u

cos u e u du

1 cos

sin

0 e

cos 0 e

sin

(sin 0 0

cos 0 1)

sin

cos 1 e .

Таким образом, sin e 12

e sin cos .

15. Найти свертку

и e b ,

e a e b

e au e b u

du e b e b a u du

b e b a u

b a

225

16. Использование правила свертки.
Найти оригинал по изображению:		1			.
Найти оригинал по изображению:	p2	1	p 1		.

Изображение может быть записано в виде				1		1	.
Изображение может быть записано в виде				p2 1		p 1	.
				p2 1		p 1

Первый из сомножителей, как изображение, имеет своим оригиналом sin (см. пример 7); второй сомножитель соответст-

вует оригиналу et (пример 3). По теореме о свертке имеем

F p p p21 1 p1 1 f sin e ,

но sin e 12 e sin cos . Следовательно,

1 e sin cos .

p 1

17. Формула Дюамеля. Найти оригинал по изображению:

p a p b

p b

Изображение

имеет оригиналe a ; следовательно,

p a

e b

Пусть f e a :

проверимlime a

1 ,

p b

т.е. соответствует условию. Тогда

e 0

e b ae au e b u du

p a

e b ae b e b a u du e b ae b

e b a u

b a

226

b a

be b aea

b a

18. Решим дифференциальное уравнение: y ay f (в про-

странствеоригиналов).

Переведем уравнение в пространство изображений, используя формулу дифференцирования (5):

p Y ( p) y( 0)

изображение_ y

a Y ( p)

изображение_ y

	( p)	(8)

изображение_ f ( )

y 0 – по сути это начальное условие. Преимуществом опера-

ционного метода решения дифференциальных уравнений является то, что начальные условия учитываются сразу при решении.

Допустим, что в случае (8) y 0 0 . ВыделимY p :

			Y p p a p .			(9)
Отсюда		Y p	1	p .	Это умножение изображений:
Отсюда		Y p	p a	p .	Это умножение изображений:
			p a
e a	1	и f p .
e a	p a	и f p .
	p a

Обратимся к определению свертки (см. правило 9):

Для решения уравнения y e a f надо найти свертку двух функций (естественно, f должна существовать и должна

быть конкретной функцией).

Достаточно часто это умножение изображений получается в виде табулированной функции из таблиц преобразования. В этом случае решение y(τ) может быть найдено сразу. Иногда функцию y(τ) называют выходной функцией, а f(τ) – входной или возбуждением. В последнем случае y(τ) будет называться откликом системы, описываемой данным дифференциальным уравнением, на возбуждение f(τ).

227

19. Решим уравнение (106), представленное в пространстве оригиналов:

1	d 2C(z)	dC(z)	k Cn (z).	(10)
Pe
	dz2	dz

Аналогично (8) с учетом (5) переведем это уравнение в пространство изображений, принимая n = 1:

Pe1 ( p2 Ц( p) p C( 0) C(1) (0))

( p Ц( p) C( 0)) k Ц( p).

Обозначим А = С(1)(+0), В = С(+0). В этом случае Ц(р) может быть выделена в виде

Ц( p)	p B A Pe B	.	(11)

	p2 p Pe k Pe

Это выражение может быть представлено в виде суммы двух дробей:

p B A Pe B	p B	A Pe B	. (12)
p2 p Pe k Pe	p2 p Pe k Pe	p2 p Pe k Pe

Разложим первую из них на элементарные дроби. Знаменатель может быть представлен в виде произведения

(р – р1)(р – р2), где р1 и р2 – корни квадратного уравнения:

	p2 Pe p Pe k 0.							(13)
p		Pe D	;	p			Pe D	,
					2
1	2					2

здесь D Pe2 4 k Pe .

Остается только подобрать коэффициенты С и Е таким образом, чтобы удовлетворялось равенство

228


p B			C		E

p p1 p p2			p p1	p p2
	C p p2 E p p1					(14)
					.
		p p1 p p2

Поскольку знаменатели дробей левой и правой частей этого равенства одинаковы, должны быть одинаковы и числители (раскрываем скобки и собираем подобные члены):

p C E C p2 E p1 p B.

(15)

Для удовлетворения этого равенства необходимо, чтобы

C E B; C p2 E p1 0.

(16)

Два этих выражения, рассматриваемые совместно, представляют собой систему линейных уравнений с двумя неизвестными С и Е. Разрешая систему, получаем

C	B p1		; E	B p2		.	(17)

	p	p		p	p
	1	2		1	2

При разложении второй дроби (12) следует учесть, что в равенстве (15) правая часть должна быть заменена на А – Ре·В. При этом, естественно, поменяются и соотношения (16).

Таким образом, исходное выражение (11) будет разложено на четыре элементарные дроби, каждая из которых может быть подвергнута обратному преобразованию Лапласа для нахождения полного выражения для оригинала. Проведя эти операции, получим

			1
1			4Pe k Pe2 2
C(z) exp	2	Pe z	Pe 4k
	2		Pe 4k

229

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 2223 / 2423 24 > Следующая >>>

Соседние файлы в папке книги