книги / Практические задания по сопротивлению материалов

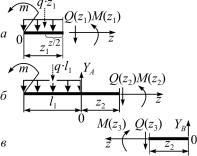
2. Определяем величину внутренней поперечной силы Q(z) по участкам балки методом сечений.

Разбиваем балку на участки. Границы участков – точки приложения сосредоточенных сил и пар сил, начало и конец распределенной нагрузки. Рассматриваемая балка имеет III участка(см. рис. 7.9, а).

Определяем значение Q(z) на каждом участке.

I участок: 0 ≤ z1 ≤ l1. Проводим секущую линию на

расстоянии z1 от левой границы участка. Часть балки справа от сечения мысленно отбрасываем, а ее действие компенсируем внутренней поперечной силой Q(z1) (рис. 7.10, а).

По III закону Ньютона величина этой силы равна суммарному действию внешних поперечных сил слева отсечения.

Составим уравнение проекций всех сил, расположенных слева от сечения, на ось y с учетом правила знаков: Q(z1) = –q·z1.

Величина Q(z1) линейно зависит от величины координаты z1. Очевидно, что эпюра Q(z1) будет представлять прямую, наклонную к оси z. Для построения эпюры поперечной силы на I участке достаточно определить значения силы Q(z1) в начале и в конце участка:

при z1 = 0 Q(0) = –q·0 = 0;

при z1 = l1 Q(l1) = –q l1 = –3 ·3 = –9 кН.

Если эпюра Q(z) пересекает ось z в некоторой точке К, необходимо найти значение zК из уравнения Q(zК) = 0, так как оно понадобится в дальнейшем при нахождении значений изгибающих моментов на этом участке (см. решение задачи 7.1 (а)).

II участок: 0 ≤ z2 ≤ l2.

Проводим секущую линию на расстоянии z2 от левой границы участка. Часть балки справа от сечения мысленно отбрасываем, а ее действие компенсируем внутренней поперечной силой Q(z2)

121

(рис. 7.10, б). Уравнение проекций всех сил, расположенных слева от сечения, на ось y:

Q(z2) = –q·l1 +YА = –3 ·3 +16,9 = 7,9 кН.

Величина Q(z2) на этом участке не зависит от величины координаты z2. ЭпюраQ(z2) будетпредставлятьпрямую, параллельнуюосиz.

III участок: для упрощения расчетов рассмотрим правую часть

балки 0 ≤ z3 ≤ l3.

Проводим секущую линию на расстоянии z3 от правой границы участка. Часть балки слева от сечения мысленно отбрасываем, а ее действиекомпенсируемвнутреннейпоперечнойсилойQ(z3) (рис. 7.10, в).

Уравнение проекций сил, расположенных справа от сечения, на ось y:

Q(z3) = –YВ = –2,1 кН.

Величина Q(z3) на этом участке не зависит от величины координаты z3. ЭпюраQ(z3) будетпредставлятьпрямую, параллельнуюоси z.

Строим эпюру поперечных сил Q(z) (рис. 7.9, б).

3. Определяем величину внутреннего изгибающего момента Mиз по участкам балки.

I участок: 0 ≤ z1 ≤ l1.

Компенсируем момент, создаваемый правой (отброшенной) частью балки внутренним изгибающим моментом Mиз(z1). Величина этого момента равна суммарному действию внешних изгибающих моментов слева от сечения (см. рис. 7.10, а). Составим уравнение проекций моментов всех сил и пар сил, расположенных слева от сечения, на ось z с учетом правила знаков: Mиз(z1) = –m –q·z1 · z1/2.

Для самопроверки определим, выполняются ли на участке диф-

d ( q·z1 ) q . Зависимости выполняются. dz

122

Эпюра Mиз(z1) будет представлять собой параболу. Для построения параболы необходимо определить значения Mиз(z1) в трех точках:

–в начале участка (z1 = 0),

–в конце участка (z1 = l1),

–в середине участка (z1 = l1/2), если эпюра Q(z1) не пересекает ось z на данном участке, или в точке К (z1 = zК), если эпюра Q(z1) пересекает осьz наданномучасткев точкеК(см. решение задачи7.1 (а):

при z1 = 0 Mиз(0) = –m – q·0 = –2,0 кН·м;

при z1 = l1 Mиз(l1) = –m – q l12 /2 = –2 – 3 ·32 /2 = –15,5 кН·м; при z1 = l1/2 Mиз(l1/2) = –m – q l12 /8 = –2 – 3 ·32 /8 = –5,4 кН·м.

II участок: 0 ≤ z2 ≤ l2.

Компенсируем момент, создаваемый правой (отброшенной) частью балки внутренним изгибающим моментом Mиз(z2) (см. рис. 7.10, б). Уравнение проекций моментов всех сил и пар сил, расположенных

слева от сечения, наось z: Mиз(z2) = –m –q l1 ·(l1/2 + z2) + YА · z2. Проверим выполнение дифференциальных зависимостей:

Зависимости выполняются.

Величина Mиз(z2) линейно зависит от величины координаты z2. Эпюра Mиз(z2) будет представлять прямую, наклонную к оси z. Для построения эпюры достаточно определить значения Mиз(z2) в начале

и в конце участка:

приz2 = 0 Mиз(0) = –m –q l1 ·(l1 /2 + 0) + YА ·0 = –2–3 ·32 /2 = –15,5 кН·м; при z2 = l2 Mиз(l2) = –m –q l1 ·(l1/2 + l2) + YА ·l2 = –2 –3 ·3 · (1,5 + 3) +

+ 16,93 ·3 = 8,3 кН·м.

III участок: рассмотрим правую часть балки 0 ≤ z3 ≤ l3. Компенсируем момент, создаваемый левой (отброшенной) частью

балки внутренним изгибающим моментом Mиз(z3) (см. рис. 7.10, в). Уравнение проекций моментов всех сил и пар сил, расположенных справаот сечения, наось z: Mиз(z3) = YВ ·z3.

123

Проверим выполнение дифференциальных зависимостей:

d 2 (YB· z3 ) d (YB ) 0 . Зависимости выполняются. dz2 dz

Величина Mиз(z3) линейно зависит от величины координаты z3. Эпюра Mиз(z3) будет представлять прямую, наклонную к оси z:

при z3 = l3 Mиз(l3) = YВ ·l3 = 2,07 ·4 =8,3 кН·м. при z2 = 0 Mиз(0) =YВ ·0 =0 кН·м;

Строим эпюру изгибающих моментов Mиз(z) (рис. 7.9, в).

4. Определяем минимальный размер сечения балки из условия прочности по нормальным напряжениям в опасном сечении

( Mизmax (z) 15,5 кН м):

В соответствии с ГОСТ 8239–89 и ГОСТ 8240–97 подбираем номер профиля балки:

–двутавр № 18: Wx = 143,0 см3.

–швеллер № 18а: Wx = 132,0 см3.

5. Проверяем прочность швеллера (как менее прочного) по касательным напряжениям в опасном сечении.

Параметры швеллера № 18а (ГОСТ 8240–97) (рис. 7.11): Wx = 132,0 см3; Jx = 1190,0 см4; Sx = 76,1 см3; s = 5,1 мм.

Допускаемые касательные напряжения для ма-

териала балки: [ ]из = 0,6[σ]из = 0,6 ·120 = 72 МПа.

Согласно эпюре поперечных сил (см. рис. 7.9, б) касательные напряжения достигают максимального значения в сечении z = l1 = 3 м( Qmax = 9 кН).

Согласно эпюре распределения напряжений по сечению балки, изготовленной из швеллера (по форме аналогичной эпюре распределения напряжений по сечению двутавра), касательные

124

напряжения достигают максимального значения на нейтральной линии сечения, совпадающей с его осью симметрии (см. рис. 7.3).

Условие прочности по касательным напряжениям выполняется.

Задача 7.2. Оценить рациональность использования различных профилей сечения балок, работающих на изгиб. Выбрать наиболее рациональный профиль.

Схему балки и данные для расчета взять из решения задачи 7.1. Геометрические характеристики сечений приведены в прил. 10.

Порядок выполнения

1. Для балки из задачи 7.1 подобрать геометрические размеры поперечного сечения, вычислить площадь A и осевой момент сопротивления Wx:

–двутаврового профиля (ГОСТ 8239–89) (см. прил. 6);

–швеллера (ГОСТ 8240–97) (см. прил. 7);

–круглого профиля (d);

–прямоугольного профиля (h/b = 2);

–квадратного профиля (a a).

2.Оценить рациональность подобранных сечений по значению удельного момента сопротивления.

3.Сделать вывод (выбрать наиболее рациональное сечение).

Указания к выполнению

Для оценки рациональности сечений балок по условию прочности при изгибе вводится безразмерная величина, характеризующая отно-

125

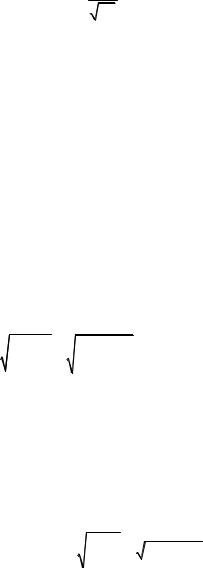
шение прочности балки по нормальным напряжениям к ее весу, – удельныймомент сопротивления:

w Wx ,

A3

где Wx – момент сопротивления сечения балки относительно нейтральной линии; А – площадь сечения балки.

Чем больше значение w, тем выше рациональность сечения (способность сопротивляться деформации изгиба при том же весе).

Пример решения задачи 7.2

Дано: на двухопорную балку (см. рис. 7.9, а) действуют поперечные силы и изгибающие моменты. Минимальный допустимый осевой момент сопротивления балки согласно решению задачи 7.1 (б)

Wxmin 129,2 см3.

Найти: наиболее рациональное сечение для балки.

Решение:

1. Определяем геометрические характеристики сечений:

а) двутавр № 18: Wx = 143,0 см3; A = 23,4 см2; б) швеллер № 18а: Wx = 132,0 см3; A = 22,2 см2;

в) круг: Wx = π·d3 / 32, следовательно,

округляем согласно ГОСТ 6636–69 (см. прил. 2) d = 11 см.

округляем согласно ГОСТ 6636–69 (см. прил. 2) b = 6,0 см,

126

Wx = b·h2 / 6 = 2·6,03 / 3 = 144 см3; A = b · h = 2 · b2 = 2 · 6,02 = 72,0 см2;

д) квадрат:

Wx = a3 / 6; a 3 6 Wx 3 6 129,2 9,2 см;

округляем, согласно ГОСТ 6636–69 (см. прил. 2) a = 9,5 см.

Wx = a3 / 6 = 9,53 / 6 = 142,9 см3; A = a2 = 9,52 = 90,3 см2.

2. Оцениваем рациональность выбранных сечений по формуле

w Wx :

A3

По степени рациональности сечения соотносятся следующим образом: wшв : wдв : wпр : wкв : wкр = 1,26 : 1,26 : 0,24 : 0,17 : 0,14 =

= 9 : 9 : 1,7 : 1,2 : 1.

Вывод: по условию прочности наиболее рациональные формы сечения – швеллер и двутавр, наименее рациональная – круг (примерно в 9 раз).

Задача 7.3. Защемленная балка находится под действием системы сил и моментов. Определить прогиб y(z) и угол поворота (z) свободного конца балки методом начальных параметров. Схему балки и

127

данные для расчета взять из решения задачи 7.1. Модуль Юнга принять Е = 2·105 МПа. Допускаемый прогиб балки [f] = l / 300 м.

Порядок выполнения

1.Начертить схему балки в масштабе с указанием числовых значений размеров, реакций в опорах (определенных при решении задачи 7.1) и приложенных сил.

2.При необходимости дополнить распределенную нагрузку до конца балки и компенсировать ее распределенной нагрузкой обратного знака.

3. Составить универсальные уравнения углов поворота (z)

ипрогибов y(z) сечений балки.

4.Определить из условий закрепления балки начальные пара-

метры 0, y0.

5.Определить угол поворота и прогиб свободного конца балки.

6.Проверить выполнение условия жесткости.

7.Скорректировать размеры балки при необходимости.

Указания к выполнению

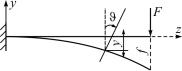
При изгибе ось балки искривляется, а поперечные сечения перемещаются перпендикулярно к ее оси на величину y и поворачиваются вокругсвоих нейтральных линий на некоторый угол (рис. 7.12).

Плоскую кривую, проведенную через центры тяжести всех сечений

ференциальным уравнением упругой линии.

Таким образом, при изгибе балки различают два вида перемещений:

1. Прогиб y(z) – линейное перемещение центров тяжести сечений балки в направлении перпендикулярном к недеформированной оси. Наибольшее перемещение называется стрелой прогиба и обозначается f. Прогиб считается положительным, если сечение смещается вверх, и отрицательным, если вниз.

128

2. Угол поворота (z) – угол, на который поворачиваются поперечные сечения балки по отношению к своему первоначальному положению. Угол поворота считается положительным, если поворот сечения происходит против часовой стрелки, и отрицательным, если по часовой стрелке.

Между прогибом балки и углом поворота сечения существует дифференциальная зависимость. При малых углах поворота можно принять

(z) dy(z) . dz

Отсюда следует, что в сечении с максимальным прогибом (ymax) угол поворота сечения равен нулю ( = 0), так как в этой точке касательная к упругой линии параллельна оси z.

Таким образом, определить прогиб балки y(z) и угол поворота сечения (z) можно, дважды интегрируя уравнение упругой линии:

здесь C и D – постоянные интегрирования, определяемые из условий закрепления балки.

Проверочный расчет на жесткость осуществляется по условию жесткости:

f f ,

где f – стрела прогиба ( f = ymax); f – допускаемый прогиб, задается

129

1

- допускаемый относительный прогиб, является справочной

n0

величиной, в зависимости от назначения конструкции принимает значения 1/150 – 1/10000.

Иногда ставится дополнительное условие жесткости – ограничение угла поворота опорных сечений:

max ,

где – допускаемый угол поворота, является справочной величиной, в среднем составляет 0,01–0,001 рад.

Для балок постоянного поперечного сечения для нахождения функций прогибов y(z) и углов поворота (z) удобно применять метод начальных параметров, суть которого состоит в составлении

универсальных (обобщенных) уравнений прогибов и углов поворота.

В этом случае обобщенное уравнение моментов относительно крайнего сечения балки примет вид:

здесь E – модуль продольной упругости материала балки (модуль Юнга); Jx – момент инерции сечения балки относительно оси x;

130