книги / Теория вероятностей и математическая статистика. Прикладная статистика с использованием MS EXCEL

Таким образом, получен доверительный интервал для математического ожидания нормально распределенной совокупности при неизвестной дисперсии, где квантиль распределения Стьюдента tβ,n−1 определяется по соответствующей таблице [2]

при заданных п и β или с помощью, например, MS Excel:

Здесьвеличинойошибки, аналогичной(2.25), являетсявеличина

Пример 2.10. Пусть объем выборки п = 25, m = 3, s = 1,5. Найти доверительный интервал для а при β = 0,99.

Решение. Из таблицы [2] находим, что для двусторонней критической области t0,99, 24 = 2,797 (β = 1 – α = 0,99, п = 25).

или 2,161< a < 3,839 – доверительный интервал, в который попадает параметр а с вероятностью 0,99.

Для данного примера MS Excel позволяет с помощью вызова функции СТЬЮДРАСПОБР (α, n – 1) найти квантиль t0,99, 24 = СТЬЮДРАСПОБР (0.01, 24) = 2,796939, вычислить

величину ошибки ε = 0,8391 по (2.23'), а затем найти границы доверительного интервала 2,1609 < a < 3,8391.

Определение доверительного интервала для среднего с помощью инструмента «Описательная статистика» MS Excel приведено ниже, в примере 2.11.

2.4.3. Доверительный интервал для оценки дисперсии нормального распределения

Если математическое ожидание mx известно, то довери-

тельный интервал для дисперсии строят, используя вспомогательную случайную величину

71

имеющую χ2n -распределение с n степенями свободы.

Здесь (σв )2 – точечная несмещенная оценка дисперсии,

вычисленная по выборке с использованием известного математического ожидания:

В более важном для практики случае неизвестного математического ожидания mx доверительный интервал для дис-

персии строят, используя аналогичную вспомогательную случайную величину

свободы.

Тогда в случае неизвестного математического ожидания mx будем иметь

72

и доверительный интервал для дисперсии при неизвестном математическом ожидании

Пример 2.11. Измерение твердости 16 образцов легированной стали в условных единицах дали следующие результаты:

В предположении, что выборка измерений получена из нормально распределенной генеральной совокупности, найти доверительные интервалы для среднего и дисперсии при доверительной вероятности 0,95.

Решение. По выборке найдем оценки

или

32,06 < m <33,08 и 0,498 < σ2 < 2,186 .

Для рассмотренного примера в MS Excel зададим в ячейках А1:А17 название переменной и ее выборочные значения. Вменю инструмента «Описательная статистика» (рис. 2.11) аналогично примеру 2.3 заказываем «Итоговую статистику» и подсчет ошибки (2.23') для доверительного интервала сред-

73

него с надежностью β = 0,95 (уровень надежности 95 %). Указываем входной интервал данных $А$1: $А$17 и выходной интервал блока ячеек для результатов $C$1: $D$16.

Рис. 2.11. Задание данных примера 2.10 в меню «Описательная статистика»

Полученные результаты в блоке ячеек C1:D16 редактируем, очищая ячейки с ненужными числовыми характеристиками и копируя в освободившиеся ячейки диапазона C1:D9 нужную информацию (рис. 2.12).

Смысл числовых характеристик блока C1:D9 приведен в табл. 2.8, за исключением величины «Уровень надежности (95,0 %)», соответствующей половине длины доверительного интервала среднего = ошибке (2.25') с указанной надежностью

β = 0,95.

Далее определяем:

– в ячейках D11:Е11 – границы доверительного интервала для среднего (= D3 – D9 = 32.066, = D3 + D9 = 33.084);

74

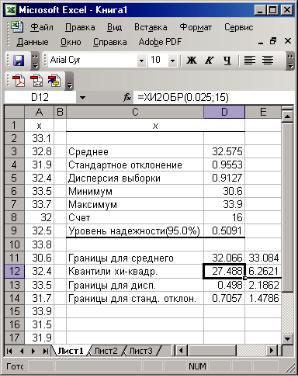
Рис. 2.12. Результаты вычислений для примера 2.10

–в ячейках D12:Е12 – нужные квантили распределения

χ2n−1 :

–в ячейках D13:Е13 – границы доверительного интервала для дисперсии (15*D5 / D12 = 0.498, 15*D5 / Е12 = 2.1862);

–в ячейках D14:Е14 – границы доверительного интервала для среднеквадратичного отклонения с помощью математической функции Excel КОРЕНЬ(х) (КОРЕНЬ (D13) = 0.7057,

КОРЕНЬ (Е13) = 1.4786).

75

Совпадение полученных результатов свидетельствует

оправильности решений с помощью обеих подходов.

2.5.Точечная и интервальная оценки вероятности успеха для биномиального закона распределения (испытания по схеме Бернулли)

Схемой испытаний Бернулли называется последовательность n независимых испытаний при одном и том же комплексе условий, в каждом из которых с одной и той же вероятностью p = P{A} может произойти событие А (часто это называ-

ют успехом) или противоположное ему событие A (неудача, промах) с вероятностью q =1− p = P{A}.

Дискретная случайная величина Х, распределенная по биномиальному закону

является числом успехов m с вероятностью успеха р при проведении n независимых опытов ( Cnm – число сочетаний из n по

mэлементов).

Вматематической статистике доказано, что относитель-

ная частота p = nA / n появления события А в n независимых

испытаниях является несмещенной, состоятельной и эффективной оценкой вероятности р = Р{А} этого события и, следовательно, точечной оценкой параметра биномиального распределения (2.33).

Интервальной оценкой неизвестного параметра биномиального распределения р с надежностью β по относительной

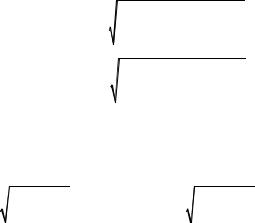
(см. пояснения к формуле (1.7) подразд. 1.2.1):

76

При большом числе испытаний n (порядка сотен) приближенные границы доверительного интервала можно вычислять более простым способом:

прибора на заданный гарантийный срок службы с неизвестной, но одинаковой вероятностью р события, что прибор отработает гарантийный срок эксплуатации. Найти доверительный интервал для оценки вероятности р с надежностью 0,95, если 54 прибора выдержало испытания.

Решение. По условию n = 60, p = nA / n = 54/60 = 0,9,

β = 0,95. Находим по справочным таблицам или с помощью вызова функции MS Exsel НОРМСТОБР (0.975) (см. пример 1.2) квантиль u0,975 = 1,95996 ≈ 1,96.

Подставляя все числовые значения в (2.34), получим p1 = 0,7985 ≈ 0,80, p2 = 0,9534 ≈ 0,95. Найденный доверитель-

ный интервал 0,80 < p < 0,95 несимметричен относительно p .

Пример 2.13. При испытаниях 1000 элементов зарегистрировано 10 отказов. Найти доверительный интервал, покрывающий неизвестную вероятность р отказа элемента с надеж-

ностью: а) 0,95; б) 0,99.

Решение. По условию n = 1000, p = nA / n = 10/1000 = 0,01,

β = 0,95; 0,99. Находим по справочным таблицам [2] или с помощью вызова функции MS Exsel НОРМСТОБР ( (1+ β) / 2 )

77

(см. пример 1.2) квантили u0,975 = 1,95996 ≈ 1,96; u0,995 =

= 2,5758 ≈ 2,58.

Поскольку число испытаний велико, используя (2.33), получим доверительные интервалы, симметричные относительно p и зависящие от β:

а) β = 0,95: доверительный интервал 0,0038 < p < 0,0162; б) β = 0,99: доверительный интервал 0,0019 < p < 0,0181.

Вопросы для самопроверки и защиты расчетно-графической работы № 2

1.Что такое статистический ряд?

2.Что называется размахом выборки? Что такое группированная выборка, группированный статистический ряд?

3.Что называется частотой и относительной частотой элементов выборки?

4.Что называется накопленной частотой и накопленной относительной частотой элементов выборки?

5.Дайте определение гистограммы частот, относительных частот, накопленных частот, накопленных относительных частот. Что такое кумулятивная кривая?

6.Опишите процедуру построения гистограмм в MS

Excel.

7.Дайте определение статистической (эмпирической) функции распределения случайной величины. Перечислите ее свойства.

8.Какие числовые характеристики имеет статистическое распределение случайной величины? Приведите ихопределения.

9.Что понимают под оценкой неизвестного параметра распределения?

10.Какие оценки называют точечными, интервальными?

11.Дайте определения свойств точечных оценок: состоятельности, несмещенности, эффективности.

78

12.Какой статистикой оценивается вероятность события? Каковы свойства этой оценки?

13.Какая статистика является состоятельной, несмещенной и эффективной оценкой математического ожидания?

14.Какие статистики используются для оценки дисперсии? Их свойства.

15.В чем заключеются метод наибольшего правдоподобия для нахождения точечных оценок неизвестных параметров распределения?

16.В чем заключается метод моментов для нахождения точечных оценок неизвестных параметров распределения?

17.Что понимают под доверительным интервалом точечной оценки и его доверительной вероятностью?

18.Охарактеризуйте доверительные интервалы для оценки математического ожидания нормального распределения при известной и неизвестной дисперсии.

19.Чем отличаются доверительные интервалы для оценки дисперсии нормального распределения при известном и неизвестном математическом ожидании?

20.Как вычисляется интервальная оценка вероятности успеха для испытаний по схеме Бернулли?

79

3. ПРОВЕРКА СТАТИСТИЧЕСКИХ ГИПОТЕЗ

Одна из часто встречающихся на практике задач, связанных с применением статистических методов, состоит в решении вопроса о том, должно ли на основании данной выборки быть принято или, напротив, отвергнуто некоторое предположение (гипотеза) относительно генеральной совокупности (случайной величины).

Например, новый метод обучения вождению с использованием компьютерного тренажера испытан на определенном числе людей. Можно ли сделать по данным результатам обучения обоснованный вывод о том, что новый метод более эффективен, чем применявшиеся ранее методы обучения? Аналогичные вопросы возникают при обосновании пользы бега трусцой, при анализе преимуществ новой модели автомобиля или модернизированного технологического процесса и т.д.

Под статистической гипотезой (или просто гипотезой)

понимают всякое высказывание (предположение) о генеральной совокупности, проверяемое по выборке.

Выдвинутая гипотеза может быть правильной или неправильной, поэтому возникает необходимость ее проверки.

Процедура сопоставления высказанного предположения (гипотезы) с выборочными данными называется проверкой гипотез (в иностранной литературе чаще используется термин

«тестирование»). Статистическими методами гипотезу можно только принять или отклонить с указанной доверительной вероятностью, но не доказать.

По своему содержанию статистические гипотезы можно подразделить на несколько основных типов:

1.Гипотезы о виде закона распределения исследуемой случайной величины.

2.Гипотезы о числовых значениях параметров случайной величины.

80