книги / Теория вероятностей и математическая статистика. Прикладная статистика с использованием MS EXCEL

нажатой ЛКМ по столбцу А до ячейки А15 задаем значения аргумента х с шагом 0,5 (способ задания арифметической прогрессии в Excel).

В ячейке В2 задаем функцию НОРМРАСП (А2; 0; 1; ИСТИНА), в ячейке С2 задаем функцию НОРМРАСП (А2; 0; 1; ЛОЖЬ), копируем формулы из ячеек В2 и С2 в ячейки В3:В14 и С3:С14 аналогично примеру 1.1. Результаты показаны на рис. 1.6, б в столбцах В и С.

Приведенные примеры показывают эффективность использования MS Excel для вычисления значений функций нормального распределения и их квантилей в сравнении с рассмотренным выше использованием табулированной нормированной функции Лапласа Ф0 (х).

1.2.2. Распределение χ2

Распределение χ2 случайной величины Х определяется плотностью вероятностей:

где ν ≥1 – число степеней свободы – параметр, определяющий

∞

распределение; Γ(z) = ∫ yz−1 exp(− y)d y – гамма-функция.

0

Случайные величины, имеющие распределение χ2 с ν степенями свободы, обозначают χν2 . Математическое ожидание и дисперсия распределения χν2 равны соответственно ν и 2ν. График этой функции при различных значениях ν приведен на рис. 1.7.

21

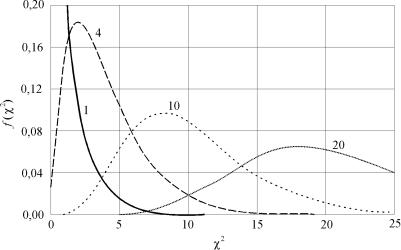
Рис. 1.7. Плотность χ2-распределения для различных степеней свободы ν = 1; 4; 10; 20

Многочисленные применения χ2-распределения в теории

вероятностей и математической статистике основаны на следующей его интерпретации.

Пусть X1, X2 , X3 , ..., Xn – случайные величины, имеющие стандартное нормальное распределение

Xi ~ N (0;1), i =1,2, ...,ν.

ν (ν ≤ 30) находятся с помощью справочных таблиц или с помощью прикладных пакетов программ.

22

Распределение χ2 при больших значениях ν (ν > 30) с достаточной для практических расчетов точностью аппроксимируется нормальным распределением N (ν;2ν), или, другими словами, распределение χ2 асимптотически нормально со средним ν и дисперсией 2ν. Для вычисления квантилей рас-

го распределения (1.3).

В табличном процессоре MS Excel 2003 для работы с распределением χ2 используются следующие две статистические функции (см. прил. 2):

–ХИ2РАСП (х; ν) – возвращает Р{X > x} = 1 – F(x) (одностороннюю вероятность) дляраспределенияχν2 ;

–ХИ2ОБР (р; ν) – возвращает значение, обратное односторонней вероятности распределения χ2 (Р{X > x} = 1 – F(x) =

=р) – квантиль x1−p, ν дляраспределенияχν2 .

Пример 1.4. Вычислить с помощью функции ХИ2РАСП (х; ν) функцию распределения F(x) распределенияχ32 , а с по-

мощью функции ХИ2ОБР (р; ν) для полученных значений F(x) = Р{X < x} = p вычислить квантили уровня р этого распределения для значений х от 0 до 5 с шагом 0,5.

Решение: Зададим в ячейках A1:C1 названия столбцов, в А2 – значение 0, в А3 – значение 0,5, выделим эти обе ячейки

23

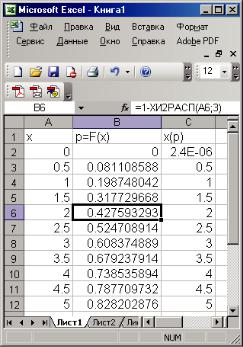
и протаскиванием черного крестика – маркера заполнения при нажатой ЛКМ по столбцу А до ячейки А13 задаем значения аргумента х с шагом 0,5. В ячейке В2 задаем функцию 1–ХИ2РАСП (А2; 3), в ячейке С2 задаем функцию ХИ2ОБР (1–В2; 3), копируем формулу из ячейки В2 в ячейки В3:В12, а затем формулу из С2 в С3:С12 аналогично примеру 1.1. Результаты показаны на рис. 1.8 в столбцах В и С.

Рис. 1.8. Результаты вычислений для примера 1.4

Следовательно, при практическом нахождении квантилей

мент «вероятность р» в ХИ2ОБР (р; ν) следует задавать через вероятность противоположного события соответственно, как: p =1−α/ 2; p =1−1−α/ 2 = α/ z; p =1−1−α = α.

24

1.2.3. Распределение Стьюдента

Распределение Стьюдента (t-распределение) названо в честь английского математика В. Госсета, публиковавшегося под псевдонимом «Student». Распределение случайной величины Т определяется плотностью вероятностей:

ние Стьюдента симметрично относительно x = 0, при k = 1 оно

ному распределению.

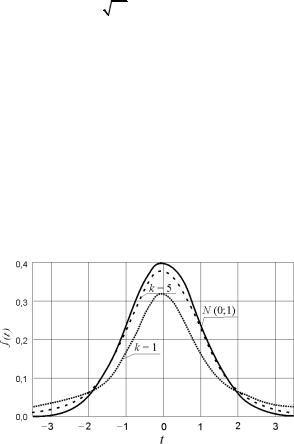
На рис. 1.9 приведены графики плотности распределения Стьюдента для трех значений k.

Рис. 1.9. Плотность распределения Стьюдента для трех значений степени свободы: k = 1; 5; ∞ [=N(0;1)]

25

Это распределение используется при малых объемах выборок для проверки гипотез и для определения доверительных интервалов. При больших значениях k (k > 30) для вычисления

квантилей распределения Стьюдента используют соотношение:

свободы.

В MS Excel 2003 вместо справочных таблиц для критических точек распределения Стьюдента, приводимых в учебниках, используются две статистические функции СТЬЮДРАСП (х; k; хвосты) и СТЬЮДРАСПОБР (р; k) (см. прил. 2), определенные только для положительной полуоси х возможных значений случайной величины Х. Свойство четности этой функции плотности распределения дает возможность вычислять необходимые величиныв области отрицательных возможных значений Х.

СТЬЮДРАСП (х; k; хвосты),

где x > 0 – численное положительное значение, для которого требуется вычислить t-распределение;

k ≥ 1 – целое, указывающее число степеней свободы; хвосты – число возвращаемых «хвостов» распределения:

– если хвосты = 1, то возвращается (вычисляется) вероятность события {X > x} с односторонним условием (критерием): СТЬЮДРАСП = P{X > x}=1 – F(x), где Х– случайная величина

сфункциейраспределенияF(x), соответствующейt-распределению;

–если хвосты = 2, то вычисляется вероятность события {|X| > x} – с двусторонним условием (критерием): СТЬЮД-

РАСП = P{|X| > x} = P{X > x ИЛИ X < –x}.

26

При x < 0 для симметричного относительно точки х = 0 t-распределения вычисление вероятностей попадания случайной точки X в заданный интервал ее возможных значений выполняется с помощью следующих формул:

P{X > x}=1 – P{X < x} = 1 – СТЬЮДРАСП(–x; k; 1); P{|X| > x} = 1 – P{|X| < x} = СТЬЮДРАСП(–x; k; 2).

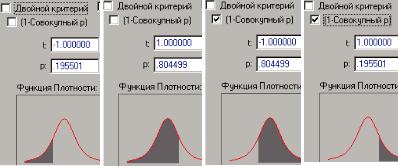
Связь вычисляемых вероятностных характеристик (вероятностей попадания случайной точки X в затемненный интервал под кривой плотности распределения на рис. 1.10–1.11) с функцией распределения Стьюдента F(x) для степени свободы k = 3 показана на подписях к этим рисункам при х = –1 и х = = 1; хвосты = 1 (рис. 1.10) и хвосты = 2 (рис. 1.11). Здесь вер-

тикальная черта в определении вероятности события имеет широко распространенное толкование – разделяет описание события и условия, при котором оно рассматривается.

Рис. 1.10. Распределения Стьюдента для степени свободы k = 3, односторонние критерии оценки вероятности (хвосты = 1)

СТЬЮДРАСПОБР (р; k),

где р – вероятность, соответствующая двустороннему критерию по распределению Стьюдента (ниже в подразд. 4.1.2, 5.1–5.2 для вероятности р следует задавать уровень значимости α =1−β –

вероятность ошибки в оценке доверительного интервала или вероятность отвергнуть верную основную гипотезу);

27

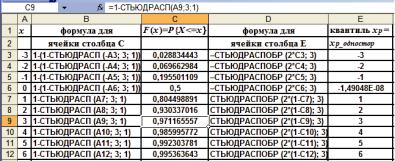
значению х находим вероятность события {X<=x}) и обратную (по заданному значению вероятности события {X<=x} находим значение квантиля уровня хр) задачи. Заданные формулы в вычисляемых ячейках С3:С12 и Е3:Е12 (их копирование в другие ячейки – способом примера 1.1) определены в соответствующих текстовых ячейках В3:В12 и D3:D12.

Результат, представленный на рис.1.12 в виде копии экранного окна, обычным копированием из MS Excel сохраним в виде табл. 1.1 для текстового редактора MS Word.

Рис. 1.12. Результаты для примера 1.5 (хвосты = 1)

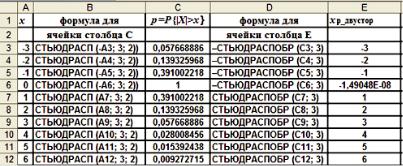
Окончание табл. 1.1

Аналогичное решение задачи для двустороннего критерия (хвосты = 2) представлено на рис. 1.13, оно обладает симметрией, показанной на рис. 1.11.

Рис. 1.13. Результаты для примера 1.5 (хвосты = 2)

Сравнение численных полученных результатов с аналогичными результатами для стандартного нормального распределения (см. рис. 1.6, а также графики рис. 1.9) показывает, что распределение Стьюдента при малом числе степеней свободы дает существенно большие вероятности при |x| > 2,5, то есть имеет существенно отличающиеся хвосты.

1.2.4. Распределение Фишера (Фишера – Снедекора)

Случайнаявеличина Fν1,ν2 поопределениюравнаотношению двухнезависимыхслучайныхвеличин χ2ν1 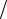ν1 и χ2ν2 ν2, тоесть

30