книги / Физика колебаний

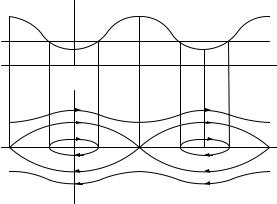
ствуют неустойчивому верхнему положению равновесия маятника – максимуму потенциальной энергии. Убегающие траектории, которые

получаются при w > ω02 , соответствуют вращательным движениям

маятника. Эти движения возникают при сообщении маятнику начального импульса, который обеспечивает прохождение маятника через верхнее положение с отличной от нуля скоростью. На фазовой плоскости это будет соответствовать выходу описывающей точки за пределы области, ограниченной кривыми C1 и C2. Эти кривые, про-

ходящие через седла и являющиеся в окрестности данных точек асимптотами гиперболических фазовых траекторий, являются сепаратрисами. Они разделяют топологически разные области на фазовой плоскости: область траекторий, приходящих из бесконечности и уходящих в бесконечность, и область замкнутых траекторий. Ограничимся в дальнейшем рассмотрением чисто колебательных движений, соответствующих замкнутым фазовым траекториям.

u(x)

x

x

C1 x

C2

Рис. 1.7

Прежде чем приступить к отысканию закона колебаний маятника, т.е. решению уравнения (1.12), найдем выражение для периода колебаний T (заметим, что T ≠ 2π/ ω0 !). Для этого применим энер-

21

(1− x)−1/ 2 =1+ 12 x + 21 34 x2 + 21 34 56 x3 =... .

После почленного интегрирования получаем выражение для периода в виде бесконечного сходящегося ряда:

С достаточной для практики точностью можно учесть только первые два члена этого ряда

На рис. 1.8 приведена зависимость относительного отклонения периода колебаний T от периода колебаний в приближении малых амплитуд как функция угловой амплитуды колебаний маятника. В данном случае мы встречаемся с зависимостью периода колебаний от их амплитуды, т.е. колебания в рассматриваемой системе являют-

ся неизохронными.

T−T0 ,%

T0

15

10

5

Рис. 1.8

23

Предполагая колебания малыми (x << l0 ), последнее выражение можно представить в виде

U (x) = kx4 = αx4 ,

8l02

где α = 8lk 2 .

0

Тогда сила, действующая на груз,

F(x) = − dU = − kx3 , dx 2l02

и уравнение колебаний приобретет вид

Это явно нелинейное уравнение при любых x. Более того, и колебания в такой системе неизохронны при любых амплитудах. Для доказательства обратимся к закону сохранения энергии

где a – амплитуда колебаний. Найдем отсюда скорость колебаний

Разрешая это уравнение относительно dt:

и интегрируя обе части полученного равенства, получим выражение для периода колебаний:

25

Если сюда подставить найденное нами выражение для U (x) , то

Введем замену переменных u = x / a. Тогда выражение для периода можно записать в виде

Этот интеграл выражается через гамма-функцию Г(z):

И для периода колебаний получаем окончательное выражение:

T =3,71 mk la0 .

Займемся теперь решением уравнения движения (1.12) (напомним, что под величиной x понимается угол отклонения маятника от положения устойчивого равновесия). Это уравнение относится к классу нелинейных дифференциальных уравнений и не существует универсальных методов их точного решения. Поэтому познакомимся с весьма распространенным методом приближенного расчета интересующей нас системы – методом последовательных приближений. Для этого выразим sin x в виде ряда

26

sin x = x − x3 +... .

6

Ограничиваясь рассмотрением значений x <<1, остановимся на члене с x3. Тогда уравнение (1.12) примет вид

( α = −1/ 6 ), будем искать решение (1.16) в виде ряда по степеням α: x = x0 +αx1 +α2 x2 +... .

Здесь x0 представляет решение уравнения (1.16) в так называемом «нулевом» приближении (при α = 0 ), x1 – первое приближение и т.д. Тогда для x0 имеем уравнение

x0 +ω02 x0 = 0 .

Однако здесь кроется ошибка. Это уравнение для определения x0 предполагает, что колебания маятника при любой амплитуде яв-

ляются изохронными, т.е. независящими от амплитуды. В действительности же, как мы установили ранее, период движения маятника с конечной амплитудой принципиально отличается от периода колебаний с бесконечно малой амплитудой. Так как величина отклонения периода T от T0 = 2π/ ω0 должна существенно зависеть от

степени нелинейности системы, вполне естественно ввести в рассмотрение новую частоту ω – частоту колебаний с заданной амплитудой в виде

ω2 = ω02 +α β+α2 β1 +... ,

27

где β, β1... – некоторые пока еще неизвестные величины. Если при расчете ограничиться первым приближением по α, то можно положить

При выбранных нами начальных условиях (x(0) = a, x(0) = 0) его решением будет

x0 = a cos ωt.

Получим теперь уравнение для первого приближения. Для этого значение x = x0 +αx1 подставим в уравнение (1.18):

(x0 +αx1 ) +ω2 (x0 +αx1 ) −αβ(x0 +αx1 ) +ω2α(x0 +αx1 )3 = 0.

Тогда, учитывая только слагаемые первой степени по α и соотношение (1.19), получаем

x1 +ω2 x1 =βx0 −ω2 x03

или

x1 +ω2 x1 =βa cosωt −ω2a3 cos3 ωt.

Воспользовавшись известным тригонометрическим преобразованием (прил. 4), можем записать

x1 +ω2 x1 =βa cosωt − 14 ω2a3 cos3ωt − 34 ω2a3 cosωt.

28

Из теории известно, что решение этого неоднородного дифференциального уравнения содержит так называемый секулярный член ~ t sin ωt, вызванный наличием в правой части уравнения члена с резонансной частотой. Ясно, что подобное решение не соответствует никакому реальному движению. Для избавления от секулярного члена выберем величину β так, чтобы

aβ− 34 a3ω2 = 0 .

Тем самым мы сразу убьем двух зайцев: устраним, во-первых, «нехорошее» решение и, во-вторых, из (1.17) можем найти значение частоты ω:

Нетрудно убедиться, что при достаточно малых амплитудах это выражение приводит к полученной нами формуле (1.15), связывающей период колебаний T с периодом T0 в линейной системе. Теперь

уравнение первого приближения для x1 запишется как

Его решение, как легко проверить, имеет вид

x1 =C1 cos ωt +C2 sin ωt + a2 cos3ωt, 32

где C1 и C2 – произвольные постоянные. Первые два слагаемых яв-

ляются общим решением однородного уравнения (1.20), а третье – частное решение неоднородного уравнения.

Полное же решение уравнения (1.16) с учетом нулевого приближения x = x0 +αx1 запишется следующим образом:

29

Значения постоянных C1 и C2 можно найти, требуя от этого

решения, чтобы оно удовлетворяло тем же начальным условиям x(0) = a, x(0) = 0 . Проделав соответствующие выкладки, получим

окончательно приближенное решение с точностью до первой степени

α (α = −1/ 6):

В найденном нами решении, которое годится для не слишком больших отклонений маятника (когда с достаточной для нас точно-

стью можно считать sin x = x − x3 / 6 ), следует отметить две особенности:

1)колебания неизохронны (частота колебаний является функцией амплитуды);

2)колебания не являются чисто синусоидальными – в них присутствуют гармоники (в нашем случае третья гармоника).

1.3.Колебания в электрическом контуре

снелинейными элементами

Рассмотрим теперь электрический колебательный контур без затухания с конденсатором, в котором нет линейной зависимости напряжения от заряда. Подобными нелинейными свойствами обладают конденсаторы, в которых в качестве диэлектрика используются сегнетоэлектрики, или емкости, возникающие в р–n-переходах полупроводниковых диодов при обратном напряжении смещения.

Как известно, для конденсаторов с сегнетоэлектриками характерно отсутствие прямой пропорциональности между зарядом q

и напряжением Uc на обкладках. Если пренебречь гистерезисом, то

30