книги / Статика в задачах биомеханики

зов руки является тяговый протез. Тяговый (механический) протез управляется с помощью тяг и полностью контролируется усилиями самого человека. Наиболее распространенные варианты тягового управления – от движения плеча, локтя, лучезапястного сустава, проксимальной фаланги пальца. Сильная сторона такого механизма – возможность контролировать усилие. При выполнении хвата пользователь сам определяет силу сжатия, скорость и может почувствовать сопротивление, когда кисть / крюк упирается в предмет и не может продолжать сдавливание. Механизм прост в управлении и обслуживании. Слабая сторона − это ограниченность силы хвата возможностями самого человека. При длительной практике ношения пользователи демонстрируют возможность манипуляции различными предметами – могут писать, пользоваться ножом и вилкой, играть втеннис, зажигатьспички, переноситьгрузит.п.

Несмотря на значительный прогресс в области протезирования, совершенный учеными и медиками за последние пару веков, остается достаточно много проблем, связанных с высокой технологичностью и сложностью подобного оборудования. Для создания протеза необходимы обширная материально-технологическая база и целая команда специалистов из различных областей: ученых, врачей, инженеров, конструкторов, программистов.

Для развития навыков и умений ставить и решать задачи проектирования протезов как руки, так и нижней конечности человека рассмотрим близкую и имеющую самостоятельное значение задачу о расчете устойчивости мобильного антропоморфного робота-манипулятора.

Расчет на устойчивость имеет важное значение при проектировании мобильных грузоподъемных механизмов. Под устойчивым понимается такое положение манипулятора, при котором любое допустимое нагружение не может привести к потере его равновесия или к опрокидыванию.

Большое влияние на устойчивость оказывает распределение массы между различными частями конструкции. Для повышения общей устойчивости робота-манипулятора часто увеличивают

41

вес его центральной части, что в большинстве случаев приводит к необоснованному перерасходу металла. Таким образом, возникает противоречивая ситуация. С одной стороны, для повышения устойчивости необходимо увеличивать вес некоторых частей машины, а с другой стороны, необходимо добиваться уменьшения обшей металлоемкости конструкции. Это возможно только путем постановки и решения соответствующей оптимальной задачи, для чего необходимо в достаточной мере владеть аппаратом теоретической механики и знать методы оптимизации.

Рассмотрим методику решения подобных задач на примере минимизации веса промышленного робота-манипулятора, широко применяемого на различных промышленных предприятиях при выполнении таких операций, как сварка, пайка, сверление, манипуляции с грузами. Это, на наш взгляд, позволит глубже разобраться в различных подходах к проблеме оптимизации конструкции антропоморфных роботов-манипуляторов, приобретающей все более важное значение для современного производства.

Условие задачи

Промышленный робот-манипулятор (рис. 1.1) размещен на горизонтально-ориентированной мобильной платформе. Расстояние между опорами мобильной платформы равно DE.

Центр тяжести мобильной платформы и основания манипулятора (общим весом РB) находится в точке B и лежит в плоскости ее симметрии (т.е. DB = BE).

Робот-манипулятор удерживает груз весом PG. Центр тяжести груза расположен в точке G. Наибольший груз, который может поднять манипулятор, имеет вес РGmax. Угол подъема груза (α) может изменяться впределах0°–80°.

Центр тяжести звеньев манипулятора (весом РC) находится в точке C. Конструкция манипулятора такова, что при подъеме груза угол наклона звеньев манипулятора β изменяется пропорционально углу α:

42

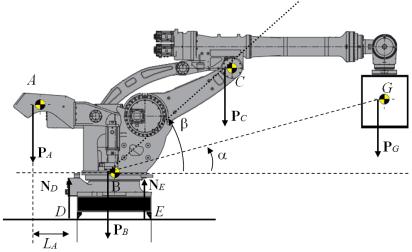
Рис. 1.1. Промышленный робот-манипулятор

Центр тяжести противовеса (весом РA) находится в точке A. Расстояние между опорой D и проекцией центра тяжести противовеса на горизонтальную плоскость обозначим LA.

Все необходимые параметры робота-манипулятора для всех вариантов заданий приведены в табл. 1.1.

Таблица 1.1

Параметры робота-манипулятора

Окончание табл. 1.1

Требуется определить вес основания манипулятора (РB), положение (расстояние LA) и вес (РА) противовеса, при которых общий вес робота-манипулятора будет минимальным. Считается, что размеры и вес звеньев манипулятора неизменны, а действием динамических сил можно пренебречь. При этом должны выполняться следующие условия устойчивости манипулятора:

ND ≥ δ,

NE ≥ δ, (1.137)РG [0, РGmax],

α [0°, +80°],

где ND, NE – реакции опоры в точках D и E, направленные по нормали к опорной поверхности; δ − некоторая положительная величина,

44

характеризующая заданный запас на устойчивость мобильного ро- бота-манипулятора; РG – вес груза; α – уголподъема груза.

Условия (1.137) должны выполнятся одновременно. Очевидно, что при максимальном весе поднимаемого груза

РGmax и угле α, равном 0°, вес противовеса РA также должен быть наибольшим. Однако вес противовеса не должен быть слишком велик, иначе робот-манипулятор может опрокинуться в тот момент, когда он находится без груза, а звенья манипулятора подняты в верхнее положение. Понятно, что в данном случае необходимы постановка и решение задачи оптимизации.

Постановка задачи оптимизации

Исходя из условий задачи, в качестве критерия оптимизации выберем общий вес манипулятора (Робщ):

Теперь данную задачу можно сформулировать как задачу минимизации с ограничениями: необходимо найти вес основания (РB), вес (РA) противовеса и положение (LA) противовеса, доставляющие минимум следующему критерию оптимизации:

LA ,PB ,PA

При ограничениях (1.137), обеспечивающих устойчивость конструкции, и ограничениях, накладываемых на искомые величины:

Lmin ≤ LA ≤ Lmax.

Искомые величины LA, РB, РA называют параметрами оптимизации. Как следует из теории оптимизации [25, 41], задача относится к задаче линейного программирования в том случае, если

45

минимизируемая функция и ограничения являются линейными относительно параметров оптимизации. В противном случае задача является задачей нелинейного программирования.

Для определения условий выполнения ограничений (1.137) необходимо составить уравнения моментов всех сил, действующих на робот-манипулятор, относительно точек D и E. Нетрудно заметить, что, поскольку в эти уравнения войдут произведения параметров оптимизации, это делает ограничения (1.137) нелинейными. Поставленная задача оптимизации (1.137)–(1.140) в этом случае является задачей нелинейного программирования. Однако если расстояние LA принимает заданное значение, то данная оптимальная задача превращается в задачу линейного программирования. Это может быть использовано при ее решении.

Метод решения задачи оптимизации

В данном учебном пособии предусмотрено несколько способов решения поставленной оптимальной задачи.

Первый способ выполнения расчетной работы предполагает, что положение противовеса известно и расстояние LA берется из таблицы. В этом случае оптимальная задача (1.137)–(1.140) является задачей линейного программирования и ее решение получается аналитически, без привлечения ЭВМ. Как известно [25], основным методом решения подобных задач является симплекс-метод. Идея этого метода состоит в построении допустимого многогранника и упорядоченном исследовании его вершин. Под допустимым многогранником в этом случае понимается область допустимых решений оптимальной задачи, образуемая пересечением m множеств. Каждое из них определяется соответствующимнеравенством:

и представляет собой полупространство, лежащее по одну сторону от гиперплоскости:

46

В выражениях (1.141), (1.142) под xj, j = 1,n, понимается со-

вокупность параметров оптимизации; aij, bi (i = 1,m , j = 1,n ) есть

заданные константы.

Из теории линейного программирования известно [25], что решение оптимальной задачи находится в одной из вершин такого многогранника.

Применение симплекс-метода рассмотрим на примере данной задачи (1.137)–(1.140) при фиксированном значении величины LA. В этом случае останется только два параметра оптимизации РA и РB. В соответствии с уравнениями (1.137), ограничения

Рис. 1.2. Допустимый многогранник в пространстве переменных РA и РB

В соответствии с системой неравенств (1.143), нетрудно построить допустимый многогранник в пространстве переменных РA и РB. Пример построения такого многогранника показан на рис. 1.2. Здесь множество допустимых решений задачи неограни-

47

ченно. Из рисунка видно, что решением задачи может быть только точка Q1 или точка Q2. Окончательный выбор решения зависит от угла наклона прямой a21PA + a22PB = b2 к оси абсцисс. В данном случае оптимальное решение задачи находится в точке Q1.

При выполнении расчетной работы вторым способом расстояние LA считается искомой величиной и решение задачи усложняется. В этом случае аналитическое решение затруднено и предполагается использование ЭВМ.

Решение задачи вторым способом заключается в том, что решение задачи нелинейного программирования заменяется решением последовательности задач линейного программирования при различных фиксированных значениях параметра LA. В этом случае отрезок [Lmin, Lmax] разбивается на N участков. Далее задача линейного программирования решается N раз с помощью сим- плекс-метода. На каждом шаге определяются оптимальные РAi и РBi и анализируется величина критерия оптимальности. То решение (РAK, РBK, LAK), при котором общий вес манипулятора будет наименьшим, считается оптимальным. Точность решения задачи в данном случае зависит от числа разбиений отрезка [Lmin, Lmax], поэтому здесь выгодно использование ЭВМ.

Для этого необходимо разработать алгоритм решения, основанный на многократном использовании симплекс-метода. Как было показано выше, решение задачи линейного программирования при фиксированном значении параметра LA находится в точке пересечения прямых:

где коэффициенты aij (i, j = 1,2) зависят от расстояния LA. Для решения задачи необходимо аналитически разрешить систему двух алгебраических уравнений относительно весов РA и РB как функций от параметра LA. Иными словами, решение системы уравнений (1.144)–(1.145) необходимо записать в виде

48

Отметим, что функции РB(LA) и РA(LA) лучше представить в явном виде, который зависит от исходных данных задачи.

Далее, организовав перебор параметра LA [Lmin, Lmax], можно легко найти оптимальное решение задачи. Конечно, последнюю операцию, требующую больших вычислений, удобно поручить ЭВМ. С этой целью предлагается составить небольшую программу, реализующую приведенный выше алгоритм, и получить решение задачи с помощью ЭВМ.

Порядок решения задачи

1.Ознакомиться с методами решения задач статики твердого тела и методами оптимизации по приведенному списку литературы.

2.Начертить расчетную схему промышленного робота-ма- нипулятора с указанием всех размеров, сил и реакции связей, действующих на элементы конструкции. Исходные данные задачи взять из приведенной таблицы (см. табл. 1.1) согласно выданному варианту и способу выполнения расчетной работы.

3.Из условий равновесия [13, 29, 33, 43] найти зависимо-

сти значений давления робота-манипулятора на опоры ND и NE от параметров PA, PB, PC, РGmax, LA. Получить условия устойчи-

вости робота-манипулятора (1.137), не забывая, что при его работе может изменяться как угол подъема α, так и вес поднимаемого груза РG.

4. Исследовать устойчивость робота-манипулятора в зависимости от веса поднимаемого груза РG [0, РGmax]. При выполнении расчетной работы первым способом величина LA берется из табл. 1.1. Затем необходимо составить систему ограничений (1.139), построить допустимый многогранник и найти оптимальное решение.

49

5.При выполнении расчетной работы вторым способом для исследования устойчивости робота-манипулятора необходимо:

а) составить систему уравнений (1.144)–(1.145), выразив ко-

эффициенты aij и bi, i, j = 1, 2, через переменную величину LA и другие параметры задачи: DE, РGmax, PC, δ;

б) cоставить для ЭВМ программу поиска оптимальных зна-

чений PA, PB и LA. При этом числе разбиений заданного отрезка [Lmin, Lmax] выбирается произвольно, но не менее 20.

в) провести расчеты на ЭВМ и получить оптимальные значения параметров PA, PB и LA.

6.Для всех способов выполнения расчетной работы проверить выполнениеусловийустойчивостиробота-манипулятора (1.137) при найденных значениях параметровоптимизации.

7.Составить отчет о работе, обязательно включающий постановку задачи оптимизации, расчетную схему, описание метода решения оптимальной задачи, анализ полученных результатов и необходимые выводы.

50