книги / Специальные главы математики
..pdf
u(t, x) T (t)X (x) . |
(3.17) |
Так как условия (3.16) должны выполняться для любого t , то из (3.17) следует, что
|
X (0) |
X (l) 0 . |
(3.18) |
||
Подставим функцию (3.17) в уравнение (3.15) и перегруппиру- |
|||||
ем сомножители следующим образом: |
|
||||
|
T (t) |
|
X (x) |
. |
|
|
a2T (t) |
|
|
||
|
|
X (x) |
|
||
В левой части полученного соотношения стоит функция, зависящая только от t , в правой – функция только от x . Переменные t и x неза-
висимы, значит, равенство возможно только в случае, если обе эти
функции постоянны. Обозначим их общее значение числом |
: |
||||
|
T (t) |
|
X (x) |
const . |
(3.19) |
|
|
|
|
||
|
a2T (t) |
|
X (x) |
||
|
|
|
|
||
Из (3.19) с учетом (3.18) получаем для функции X (x) краевую задачу
X (x) |
X (x), |
(3.20) |
|
Х (0) |
Х (l) 0, |
||
|
которая, как нетрудно заметить, имеет нетривиальные решения только
при |
2 |
0 . Как известно из курса обыкновенных дифференци- |
||||||
|
||||||||
альных уравнений, общее решение уравнения X (x) |
2 X (x) |
|
||||||
представляется в виде X (x) Аcos |
x Bsin |
|
x . |
|
|
|
||
Учитывая условия (3.18), находим, |
что A |
|
0, |
n l , n |
Ґ , |
а B – |
||
любое |
число. Следовательно, при |
всех |
n |
n l 2 , n |
Ґ |
задача |
||
|
|
|
|
|
|
|
|
|
(3.20) имеет нетривиальные решения Xn (x) |
|
Bn sin( |
nх l) . |
|
|
|||
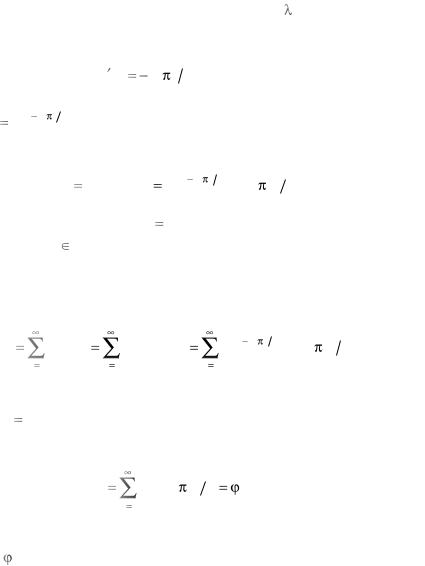
Вернемся к уравнению (3.19) и для каждого |
n |
найдем соот- |
|||||
|
|
|
|
|
|
|
|
ветствующую ему функцию |
|
Tn (t) |
как решение дифференциального |
||||
уравнения |
|
|
|
|
|
|
|
|
|
T (t) |
|
a n l 2 T (t) , |
|
|
|
т.е. T (t) |
T e a n l 2 t , |
где T |
|
– произвольные постоянные. Из пред- |
|||
n |
n |
n |
|
|
|
|
|
ставления (3.17) получаем, что |
|
|
|
||||
|
u (t, x) |
T (t) X |
n |
(x) |
C e a n l 2 t sin( nх l) , |
|
|
|
n |
n |
|
n |
|
|
|
где для |
удобства положено |
|
Сn |
Tn Bn . Подчеркнем, |
что любая из |
||
функций un (t, x), n Ґ является решением уравнения (3.15), удовле-
творяющим краевым условиям (3.16). Раз так, то и любая их линейная комбинация есть решение задачи (3.15)–(3.16). Составим бесконечную сумму
u(t, x) |
u |
n |
(t, x) |
T (t) X |
n |
(x) |
C e a n l 2 t sin( nх l) |
|
|
|
n |
|
n |
||
n 1 |
|
|
n 1 |
|
|
|
n 1 |
и покажем, что коэффициенты Сn в ней можно выбрать так, что для
функции u |
u(t, x) будет выполнено условие (3.5) (вот теперь о нем |
|
следует вспомнить!): |
|
|
|
u(0, x) |
Cn sin( nх l) (x) . |
|
|
n 1 |
Полученное равенство есть не что иное как представление |
||
функции |
(х) рядом Фурье (по синусам) на конечном отрезке 0,l ; |
|
для коэффициентов такого ряда давно найдены формулы (коэффициенты Фурье):
|
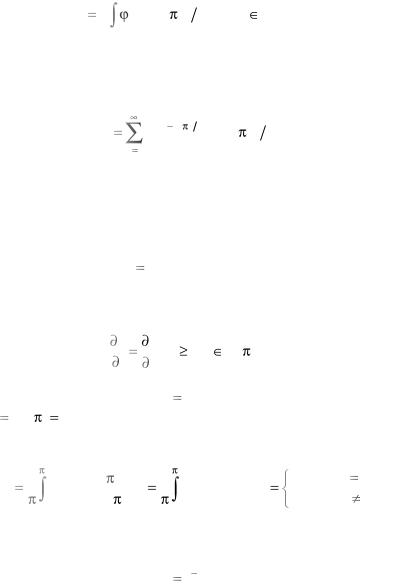
2 l |
|
||
Cn |
|
(x)sin( nх l) dx, n Ґ . |
(3.21) |
|
l |
||||
|
0 |
|
||
Итак, мы получили решение поставленной задачи в виде бесконечного ряда:
u(t, x) |
C e a n l 2 t sin( nх l) , |
(3.22) |
|
n |
|
|
n 1 |
|
коэффициенты которого находятся по формулам (3.21).
Пример 13. Найти закон распространения тепла в тонком однородном стержне длины π, имеющем коэффициент температуропроводности равный 1, если начальная температура всех точек стержня задается равенством u(0, x) sin 2x , а концы стержня поддерживаются
при температуре, равной нулю.
Решение. Задача сводится к решению уравнения теплопровод-
ности
|
|
|
|
|
u |
|
|
2u |
|
|
, |
|
|
|||
|
|
|
|
|
|
|
|
|
|
, t |
0, x |
0, |
|
|
||
|
|
|
|
|
t |
x2 |
|
|
||||||||
с начальным условием |
|
u(0, x) |
sin 2x |
и |
граничными условиями |
|||||||||||
u(t,0) u(t, ) 0 . |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
По формулам (3.21) получаем: |
|
|
|
|
|||||||||||
C |
|
2 |
sin 2x sin |
nх |
dx |
2 |
|
sin 2x sin nx dx |
1, если n |
2, |
||||||
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|||||||||||
n |
|
|
|
|
|
|
|
|
|
0, если n |
2. |
|||||
|
0 |
|
|
0 |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|||||||||
По формуле (3.22) находим окончательный ответ: |
|
|
||||||||||||||
|
|
|
|
|
|
|
u(t, x) |
e 4t sin 2x . |
|
|
|
|||||
Лекция 14. Решение задачи Дирихле для прямоугольной пластинки
Рассмотрим задачу Дирихле для уравнения
2u |
|
2u |
0, (x, y) D , |
(3.23) |
x2 |
|
y2 |
||
|
|
|
если область D представляет собой прямоугольник
D (x, y) : 0 x a,0 y b . |
|
|||||||||
На границе D прямоугольника функция |
|
u(x, y) предполагается за- |
||||||||
данной: |
|
|
|
|
|
|
|
|
|
|
u(x, y) |
|
|
|
f ( y), |
u(x, y) |
|
|
|
g1(x), |
|
|
|
|
|
|
|
|
||||
|
|
x |
0 |
1 |
|
|
y |
0 |
|
(3.24) |
u(x, y) |
|
|
|
f2 ( y), |
|
|
|
|
|
|
|
x |
a |
u(x, y) |
|
y |
b |
g2 (x). |
|
||
|
|
|
|
|
|
|
||||
Будем искать решение задачи (3.23)–(3.24) в виде
u(x, y) v(x, y) w(x, y) ,
где и функция v(x, y) , и функция w(x, y) являются решениями уравнения (3.23), но с разными граничными условиями:
v(x, y) v(x, y) v(x, y) v(x, y)
x 0
xa
y0
y b
0, |
w(x, y) |
|
0, |
w(x, y) |
|
|
||
g1(x), |
w(x, y) |
|
|
||
g2 (x). |
w(x, y) |
|
|
x |
0 |
f1( y), |
|
|
|
||
x |
a |
f2 ( y), |
(3.25) |
|
|||
|
|
0, |
|
y |
0 |
|
|
|
|
||
y |
b |
0. |
|
|
|
Рассмотрим подробно процесс построения функции v(x, y) на основе метода Фурье. Представление для функции w(x, y) получим по
аналогии.
Будем искать решения уравнения (3.23), представимые в виде v(x, y) X (x)Y ( y) и удовлетворяющие условиям
v(x, y) |
|
x 0 0, v(x, y) |
|
x a 0 . |
(3.26) |
||||
|
|
|
|||||||
Так как условия (3.26) должны выполняться для любого y , то |
|
||||||||
|
|
|
X (0) |
X (a) 0 . |
(3.27) |
||||
Подставим функцию v(x, y) X (x)Y ( y) в уравнение (3.23) и |
|||||||||
перегруппируем сомножители следующим образом: |
|
||||||||
|
|
|
X (x) |
|
Y ( y) |
. |
|
||
|
|
|
|
|
|
||||
|
|
|
X (x) |
|
Y ( y) |
|
|||
В левой части полученного соотношения стоит функция, зависящая только от x , в правой – функция только от y . Переменные x и y не-
зависимы, значит, равенство возможно только в случае, если обе эти функции постоянны. Обозначим их общее значение числом :
|
X (x) |
Y ( y) |
const . |
(3.28) |
||
|
|
|
|
|
||
|
X (x) |
Y ( y) |
||||
|
|
|
||||
Из (3.28) с учетом (3.27) получаем для функции X (x) |
краевую задачу |
|||||
|
|
X (x) X (x), |
|
(3.29) |
||
|
Х (0) |
Х (a) 0, |
|
|||
|
|
|
||||
решение которой было найдено нами раньше (см.задачу (3.20)). Задача
(3.29) имеет нетривиальные решения только при |
n |
n a 2 |
, n Ґ |
, |
|
|
|
|
и эти решения с точностью до произвольного ненулевого коэффициен-
та имеют вид Xn (x) sin( nх a) . |
|
|
Вернемся к уравнению (3.28) и для каждого |
n |
найдем соот- |
|
|
ветствующую ему функцию Yn ( y) как решение дифференциального уравнения
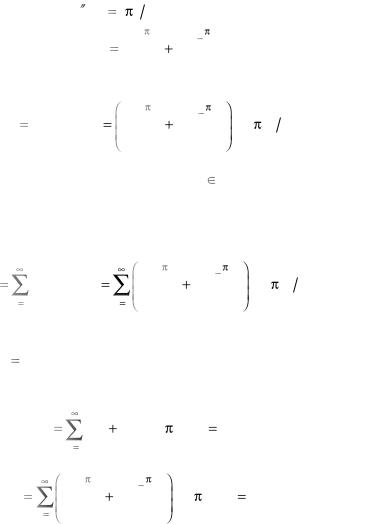
Y ( y) |
n a 2 Y ( y) . |
|
|
|
||
|
|
ny |
|
ny |
|
|
|
|
|
|
|
|
|
Легко видеть, что Y ( y) |
A e a |
B e |
a , где A , B |
– произ- |
||
n |
n |
n |
|
n n |
||
вольные постоянные. Перемножая функции Xn (x), Yn ( y) , получаем:
|
|
|
|
|
ny |
|
ny |
|
v (x, y) |
X |
n |
(x)Y ( y) |
A e a |
B e a |
sin( nх a) . |
||
n |
|
n |
n |
n |
|
|||
Подчеркнем, что любая из функций vn (t, x), n Ґ является решением
уравнения (3.23), удовлетворяющим краевым условиям (3.26). Раз так, то и любая их линейная комбинация есть решение задачи (3.23)–(3.26). Составим бесконечную сумму
|
|
|
|
|
ny |
|
ny |
|
|
|
|
|
|
|
|
|
|
v(x, y) |
X |
n |
(x)Y ( y) |
A e a |
B e a |
sin( nх a) (3.30) |
||
|
|
n |
n |
n |
|
|||
|
n 1 |
|
|
n 1 |
|
|
|
|
и покажем, что коэффициенты An , Bn в ней можно выбрать так, что для функции v v(x, y) будут выполнены оставшиеся два условия из
(3.25):
v(x,0) An Bn sin( nх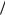
a) g1(x) ,
n 1
|
|
nb |
|
nb |
v(x,b) |
A e a |
B e a |
||
|
n |
n |
||
|
n 1 |
|
|
|
sin( nх
a) g2 (x) .
Полученные равенства есть |
представление функций |
g1(х), g2 (х) рядами Фурье (по синусам) |
на конечном отрезке 0, a ; |
коэффициенты этих рядов выражаются через функции g1(х), g2 (х) :
|
|
|
|
|
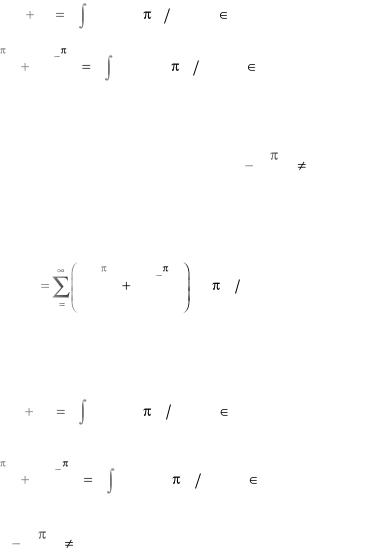
2 a |
|
|
|||
|
An |
Bn |
|
|
g1(x)sin( nх a) dx, n Ґ , |
|||||
|
a |
|||||||||
|
|
|
|
|
0 |
|
|
|
|
|
|
nb |
|
|
nb |
|
2 a |
|
|
||
A e a |
B e a |
|
(x)sin( nх a) dx, n Ґ . |
|||||||
|
|
g |
2 |
|||||||
|
|
|||||||||
n |
n |
|
|
|
a 0 |
|
||||
|
|
|
|
|
|
|
|
|
||
При каждом фиксированном n последние два равенства образуют систему линейных алгебраических уравнений относительно не-
известных A , B . Определитель этой системы равен |
sh |
nb |
0 , сле- |
|
|||
n n |
|
a |
|
|
|
||
довательно, An , Bn определяются из этой системы однозначно.
По аналогии с представлением (3.30), легко записать вид функции w(x, y) , являющейся решением второй вспомогательной задачи:
|
|
nx |
|
nx |
|
|
|
|
|
|
|
w(x, y) |
C e b |
D e b |
sin( ny b) , |
||
|
n |
n |
|
||
|
n 1 |
|
|
|
|
где коэффициенты Cn , Dn определяются из системы линейных алгебраических уравнений:
|
|
|
|
|
|
2 b |
|
|
, |
||||
|
Cn |
|
Dn |
|
|
|
f1( y)sin( ny b) dy, n Ґ |
||||||
|
|
b |
|||||||||||
|
|
|
|
|
|
0 |
|
|
|
|
|
||
|
na |
|
|
|
na |
|
2 b |
|
|
|
|||
C e b |
|
|
b |
|
|
n Ґ , |
|||||||
D e |
|
|
f |
2 |
( y)sin( ny b) dy, |
||||||||
|
|
||||||||||||
n |
|
n |
|
|
|
|
b 0 |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
||
с определителем |
sh |
na |
0 . |
|
|
|
|
|
|||||
b |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Список литературы
1.Эльсгольц Л.Э. Дифференциальные уравнения и вариационное исчислениe/ Л.Э. Эльсгольц. – М.: УРСС, 2000 (или 2003).
2.Пантелеев А.В. Вариационное исчисление в примерах и задачах/
А.В. Пантелеев.– М.: МАИ, 2000.
3.Краснов М.Л. Интегральные уравнения/ М.Л. Краснов,
А.И. Киселев, Г.И. Макаренко. – М.: Наука, 1968.
4.Краснов М.Л. Интегральные уравнения: задачи и примеры с подробными решениями/ М.Л. Краснов, А.И. Киселев, Г.И. Макаренко. – М.: УРСС, 2003.
5.Тихонов А.Н. Уравнения математической физики/ А.Н. Тихо-
нов, А.А. Самарский. – М.: МГУ, 1999.
6. Владимиров В.С. Уравнения математической физики/
В.С. Владимиров, В.В. Жаринов. – М.: Физматлит, 2003.