
книги / Специальные главы математики
..pdf
Решение. Подынтегральная функция относится ко второму ти-
пу при M t, x x , N t, x |
t , а уравнение Эйлера имеет вид: 1 1, |
||||
т.е. обращается в тождество. Но если равенство |
|||||
|
|
M |
t, x |
|
N t, x |
|
x |
t |
|||
выполняется тождественно, то, как известно из курса интегрального исчисления, это означает, что подынтегральная функция являет собой
полный дифференциал.
В данном случае его легко восстановить: x xt& d xt ; следовательно,
|
b |
|
||
f x |
d xt xt |
|
ba x b b x a a b |
a , |
|
||||
|
|
|
||
|
a |
|
||
т.е. значение функционала остается неизменным при любой дифференцируемой на a,b функции. Значит, все эти функции (их бесконечное множество) являются решениями данной вариационной задачи.
3. |
F |
F t, x& . Уравнение Эйлера имеет вид: |
d |
F |
t, x& |
0 |
|
||||||
|
|
|
dt |
x& |
|
|
|
|
|
|
|
|
|
или Fx& t, x& |
C . Таким образом, уравнение допускает понижение по- |
|||||
рядка и становится дифференциальным уравнением первого порядка. |
|
|||||
4. |
F |
F x& . Решениями уравнения Эйлера могут быть только |
||||
прямые: |
x |
c1t c2 . |
|
|
|
|
5. F F x, x& . Уравнение Эйлера снова допускает понижение порядка и принимает вид:
F x, x& xF& x& x, x& C .

Лекция 4. Обобщения уравнения Эйлера
Пользуясь теми же методами, несложно получать аналоги уравнений Эйлера для функционалов более общего вида. Остановимся на двух из них.
Функционал зависит от производных до n-го порядка
Для функционалов вида
b
f x F (t, x, x&&, x,K , x n ) dt
a
экстремали являются решениями уравнения Эйлера–Пуассона:
F |
d |
F |
d 2 |
F K ( 1) |
n d n |
F ( n) 0 . |
|
|
|
|
|
||||
x |
dt |
x& |
dt2 |
&x |
|
dtn |
x |
|
|
|
|
||||
Понятно, что для однозначного выбора экстремали требуется дополнительно задать условия на границах:
|
x(a) A , x&(a) A , K , x(n 1) (a) A |
, |
|
|||||||||
|
|
0 |
|
1 |
|
|
|
|
n 1 |
|
|
|
|
x(b) B , x&(b) B , K , x(n 1) (b) B . |
|
||||||||||
|
|
0 |
|
1 |
|
|
|
|
n 1 |
|
|
|
|
Пример 4. Найти экстремали следующего функционала |
|||||||||||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
f x |
(x |
2 |
|
|
2 |
2 |
|
|
|
|
|
|
|
|
2x& &x ) dt , |
|
|
|
|||||
|
|
|
|
0 |
|
|
|
|
|
|
|
|
удовлетворяющие условиям: x(0) |
0, x(1) |
sh1, x&(0) 0, x&(1) |
e . |
|||||||||
|
Решение. Уравнение Эйлера–Пуассона для данного функцио- |
|||||||||||
нала имеет вид 2x |
d 4x& |
d 2 2&x |
0 или x 4 |
2x 2 x |
0 . Решая |
|||||||
dt |
|
dt2 |
|
|
||||||||
|
|
|
|
|
|
|
|
|
||||
это |
уравнение, |
получаем |
|
семейство |
экстремалей |
вида: |
||||||

x t c1et c2tet c3e t c4te t . |
Учитывая граничные условия, нахо- |
|||
дим единственную экстремаль x |
t t sht . |
|||
Функционал зависит от нескольких функций |
||||
Для функционалов вида |
|
|
|
|
b |
|
|
||
f x, y |
F (t, x, x&, y, y&) dt |
|||
a |
|
|
||
экстремали являются решениями системы уравнений Эйлера: |
||||
F |
|
d |
F |
0 |
|
|
|||
x |
|
dt |
x& |
|
|
|
|
. |
|
|
|
d |
|
|
F |
|
F |
0 |
|
|
|
|||
y |
|
dt |
y& |
|
|
|
|
|
|
Соответственно, граничные условия принимают вид:
x(a) A0 , x&(a) A1, x(b) B0 , x&(b) B1.
Пример 5. Найти экстремали следующего функционала
|
2 |
|
f x, y |
2 |
2 |
(x& |
y& 2xy) dt , |
|
|
0 |
|
удовлетворяющие условиям: |
x(0) x( |
2) 1, y(0) y( 2) 1 . |
Решение. Система уравнений Эйлера–Пуассона имеет вид:
2 y |
d |
(2x&) |
0 |
|
|
|
|
|
|
&x y |
0 |
||||
dt |
|
||||||
2x |
|
d |
(2 y&) |
0 |
или |
&y x |
0 . |
|
dt |
|
|
|
|||
|
|
|
|
|
|
|
|
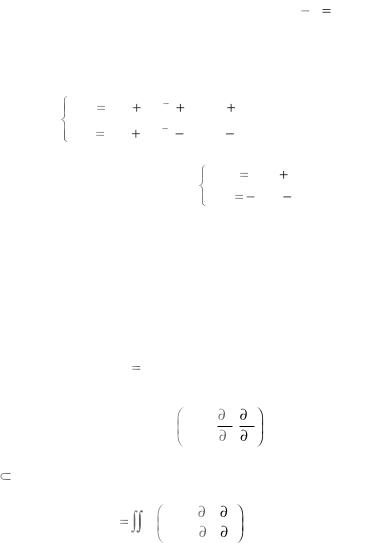
Выражая из второго уравнения x через &y и подставляя его в первое
уравнение, получаем уравнение относительно x : x(4) x 0 . Решая это уравнение, получаем семейство экстремалей x(t) , из которого
двукратным дифференцированием находим семейство экстремалей y(t) . Окончательно имеем:
x t |
c et |
c e t |
c cost |
c sin t |
|
|
|
|
1 |
2 |
3 |
|
4 |
. |
|
|
c et |
c e t |
|
|
|
|
|
y(t) |
c cost |
c sin t |
|
|
|||
|
1 |
2 |
3 |
|
4 |
|
|
Учитывая граничные условия, находим |
x t |
cost |
|
sin t . |
|||
|
|
|
|
y(t) |
cost |
sin t |
|
Вариационные задачи на плоскости и в пространстве
Функционалы, рассмотренные выше, имели областью определения множества функций одной переменной. Соответственно, уравнение Эйлера, к которому сводилась вариационная задача, представляло собой обыкновенное дифференциальное уравнение второго порядка.
Предположим, что вариационная задача должна быть поставлена и решена для функции нескольких (ради определенности – двух)
независимых переменных: x x t,s . Тогда, если мы продолжим изучение функционалов интегрального вида, то вместо функции F t,x,x&
следует рассматривать функцию F t ,s,x, xt , xs , а вместо однократ-
ного интеграла появится двойной, взятый по некоторой плоской области G Ў2 .
f x |
F t,s,x, |
x |
, |
x |
dsdt |
(1.4) |
|
t |
s |
||||||
|
G |
|
|
|
|||
|
|
|
|
|
|
Уточним условия на функцию x . Помимо непрерывности в области G вместе со своими частными производными, она должна удовлетворять граничным условиям. Остановимся на этом подробнее. В лекции 2 для однозначного определения экстремали задавались зна-

чения x a и x b , т.е. значения функции x на границах отрезка a,b . Для функции двух переменных, продолжая аналогию, естест-
венно задать условия на границе области G . Обозначим эту границу G и потребуем, чтобы
|
|
|
|
|
|
|
x |
|
t ,s |
|
G |
|
. |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
На функционал (1.4) легко обобщается необходимое условие |
|||||||||||||||||
экстремума. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Обозначим для удобства |
p |
|
x |
,q |
x |
. В этих обозначениях |
|||||||||||
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
s |
||
функция F t ,s,x, |
x |
, |
x |
примет вид |
F |
|
t,s,x, p,q . |
||||||||||
|
|
|
|||||||||||||||
|
t |
s |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Теорема 3. Пусть функция x0 |
– экстремаль функционала (1.4). |
||||||||||||||||
Тогда x0 является решением уравнения: |
|
|
|
|
|||||||||||||
|
|
|
|
F |
d |
F |
|
|
|
d |
|
F |
|
0 |
(1.5) |
||
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
x |
dt |
p |
|
|
|
ds q |
|
|
|
||||
Полученное уравнение представляет собой уравнение в частных производных второго порядка. Если функция x зависит только от одной переменной, то оно превращается в уравнение Эйлера.
Пример 6. Найти экстремаль функционала
|
|
|
|
|
x 2 |
x |
2 |
|
|||
|
|
f |
x |
|
|
|
|
|
2tx |
dsdt, |
|
G |
t |
s |
|||||||||
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
||
где G – единичный круг с центром в начале координат, с граничными |
|||||||||||
|
|
|
|
|
|
|
|
|
|||
условиями x |
|
t ,s G |
0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Решение. Пользуясь введенными ранее обозначениями, запи- |
|||||||||||
шем: F t,s,x, p,q |
p2 q2 2tx, F |
|
2t, F |
2 p, F 2q . Урав- |
|||||||
|
|
|
|
|
|
|
x |
|
p |
q |
|
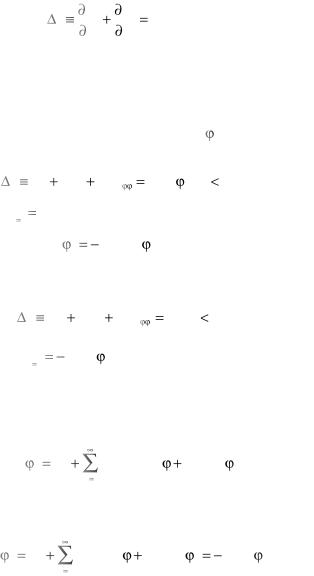
нение (1.5) имеет вид x |
2 x |
|
2 x |
t , |
то есть представляет собой |
|
t |
2 |
|
s2 |
|||
|
|
|
|
|||
уравнение эллиптического типа. Область, на которой ищется решение, есть внутренность круга (ограниченное множество), граница его – окружность, вдоль которой функция x обращается в нуль. Следовательно, искомая экстремаль является решением задачи Дирихле для внутренности круга. Для круговых областей естественно переформулиро-
вать задачу, перейдя к полярным координатам r, |
: |
||||||||||||
|
x |
x |
|
1 |
x |
1 |
x |
|
r cos , r |
1, |
|||
|
|
r2 |
|
||||||||||
|
|
|
rr |
|
r r |
|
|
|
(1.6) |
||||
x |
|
r 1 |
0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
3 |
|
|
|
|||
Заменой переменных y |
|
|
|
|
|
сводим уравнение (1.6) к од- |
|||||||
r, |
|
|
|
r |
cos |
||||||||
8 |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
нородному (с ненулевыми граничными условиями):
|
y yrr |
|
|
1 |
yr |
1 |
y |
0, r 1, |
|
|
|
|
|
2 |
|||||
|
|
|
|
|
r |
r |
(1.7) |
||
|
|
|
1 |
|
|
|
|
|
|
y |
|
r 1 |
cos . |
|
|
|
|||
|
|
|
|
||||||
|
8 |
|
|
|
|||||
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
Как известно из курса уравнений математической физики, решение задачи (1.7) имеет представление в виде ряда:
y r, |
A |
rn A cos n |
B sin n . |
|
0 |
n |
n |
|
|
n 1 |
|
Учитывая граничные условия, получаем
y 1, |
A |
A cos n |
B sin n |
1 |
cos , |
|
|||||
|
0 |
n |
n |
8 |
|
|
n 1 |
|
|
|
откуда, по формуле для коэффициентов ряда Фурье (или по теореме Стеклова), получаем:
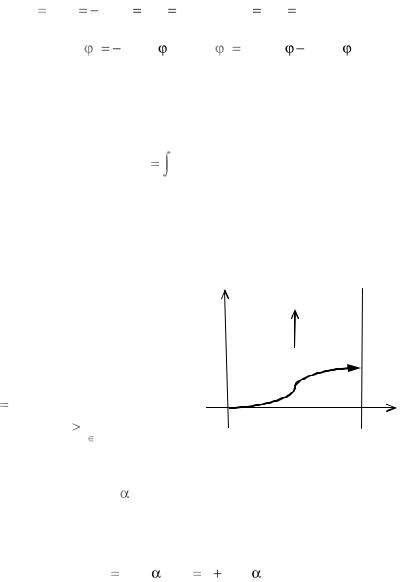
A |
0, A |
1 |
,A |
0, n 2,3,K ; B |
0, n 1,2,K . |
||||||||
|
|||||||||||||
0 |
1 |
8 |
|
n |
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Следовательно, y r, |
|
1 |
|
, а |
|
1 |
3 |
|
1 |
rcos . |
|||
|
|
|
rcos |
x r, |
|
|
r |
cos |
|
||||
|
8 |
8 |
8 |
||||||||||
|
|
|
|
|
|
|
|
|
|||||
Лекция 5. Вариационные задачи с подвижными границами
В предыдущих лекциях при исследовании функционала
b
f x F t, x, x&dt
a
предполагалось, что граничные точки (a, A) и (b, B) заданы. Подобное
предположение не всегда выполняется для многих интересных и практически важных вариационных задач. Рассмотрим в качестве примера
задачу навигации.
y
Задача навигации
В этой задаче рассматривается река ширины b с прямыми параллельными берегами. Считая один берег реки совпадающим с осью y , введем скорость течения
реки v v(x) . Лодка с постоянной
скоростью c ( c max v(x) ), за
x [0,b]
кратчайшее время должна пересечь реку, отчалив из точки O(0,0)
0 |
b |
x |
|
Рис. 2
(рис.2).
Обозначим через угол, который образует вектор скорости лодки с положительным направлением оси Ox . Тогда реальная ско-
рость движения лодки в момент времени t |
определяется равенствами |
||||
|
dx |
c cos , |
dy |
v |
c sin . |
|
dt |
dt |
|||
|
|
|
|
||
Отсюда
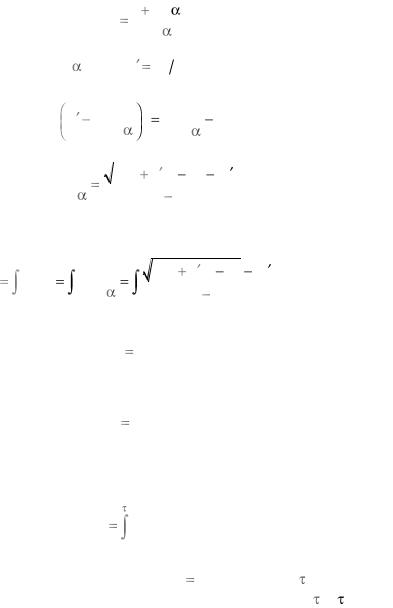
|
|
|
|
dy v |
sin |
|
, |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx |
cos |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||
что позволяет выразить |
через y |
dy dx : |
|
|
|
|
|||||||||||
|
|
|
|
|
v |
2 |
|
1 |
|
|
|
|
|||||
|
y |
|
|
|
|
|
1 |
, |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
c cos |
|
cos2 |
|
|||||||||||||
|
|
|
|
|
|
|
|
||||||||||
откуда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
1 |
|
|
|
c2 (1 |
y |
2 ) v2 vy |
. |
||||||||||
|
c cos |
|
|
|
|
|
|
|
|
c2 |
|
v2 |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Для времени пересечения реки находим
t |
b |
dt |
dx |
b |
|
0 |
dx |
0 |
|||
|
|
|
b |
|
|
|
|
|
|
|
dx |
c2 (1 y |
2 ) |
|
v2 vy |
|
|||
|
|
dx . |
||||||
c cos |
0 |
|
c2 |
|
v2 |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
Последний интеграл должен быть минимизирован за счет выбора функции y(x) при условии y(0) 0 .
Как видим, в отличие от предыдущих задач, правый конец искомой кривой заранее не определен. В действительности, выбор начальной точки движения лодки никак не сказывается на форме оптимального курса и условие y(0) 0 оказывается несущественным. Мы
приходим, таким образом, к задаче со свободными (подвижными) гра-
ницами.
Пусть в вариационной задаче об отыскании экстремума функционала
f x |
F t, x, x&dt |
(1.8) |
|
a |
|
одна граничная точка фиксирована (x(a) A) , а вторая – |
– может |
|
перемещаться (область допустимых перемещений для точки ( , x( )) в
разных задачах может быть разной). Тогда класс кривых, на которых ищется экстремум, расширяется, но вариационная задача остается со-
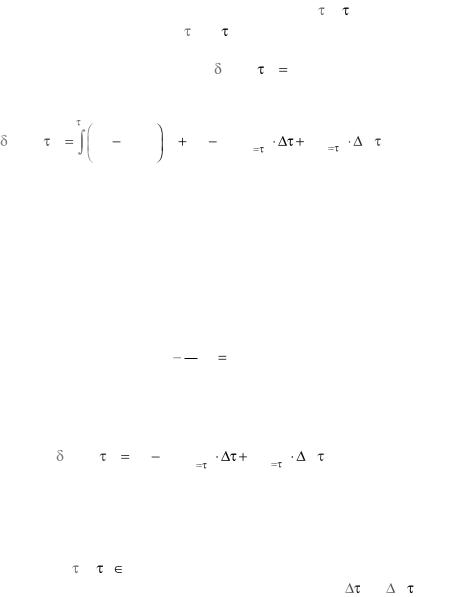
держательной. Функционал в этом случае начинает зависеть, вообще говоря, от трех переменных: функции x и параметров , x( ) .
Пусть x0 – экстремаль, ( 0 , x0 ( 0 )) – вторая граничная точка, на которой реализуется экстремум функционала (1.8). Тогда, в силу
необходимого условия экстремума, ( f )(x0 , 0 ) |
0 . Вычисляя вариа- |
|||||||||||||
цию функционала (1.8), получаем: |
|
|
|
|
|
|
|
|
||||||
|
|
|
0 |
d |
|
|
|
|
|
|
|
|
|
|
( f )(x , |
0 |
) |
F |
F |
dt F xF& |
|
|
F |
|
|
x( |
0 |
) . |
|
|
|
|
|
|||||||||||
|
|
|
|
|
||||||||||
0 |
|
x |
dt |
x& |
x& |
|
t 0 |
x& |
|
t |
0 |
|
||
|
|
|
a |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Если на какой-нибудь кривой x0 (t) достигается экстремум в
задаче с подвижными границами, то экстремум заведомо достигается на более узком классе кривых, имеющих общие граничные точки с кривой x0 (t) .
Следовательно, должно быть выполнено основное необходимое для достижения экстремума в задаче с неподвижными границами условие – функция x0 (t) должна быть решением уравнения Эйлера.
Значит, на функции x0 (t) уравнение
d
Fx dt Fx& 0
обращается в тождество. А тогда в формуле для вариации функционала (1.8) первое интегральное слагаемое обращается в нуль и вариация приобретает вид
( f )(x0 |
, 0 ) F xF& x& |
t 0 |
Fx& |
t |
x( |
0 ) |
(1.9) |
|
|
|
0 |
|
|
Для дальнейшего анализа полученной формулы целесообразно рассмотреть разные виды множеств, которым может принадлежать подвижная граничная точка.
1. Пусть ( , x( )) D , где D – некоторое плоское множество, со-
держащее внутренние точки. Тогда приращения |
и x( ) |
независимы, и для равенства нулю вариации необходимо и

достаточно |
одновременное |
выполнение |
равенств |
||||
F xF& x& |
|
|
|
|
|
|
|
|
t 0 |
0 и Fx& |
t |
0 . |
|
|
|
|
|
|
0 |
|
|
||
2.Свободная граничная точка перемещается по вертикальной прямой. Тогда 0 , и вариация равна нулю, если (и только
если) Fx&t 0 0 .
3.Свободная граничная точка перемещается по горизонтальной прямой. Тогда x( ) 0 , и необходимое условие экстремума
принимает вид F xF& x& |
t |
0 . |
|
|
0 |
4.Граничная точка ( , x( )) перемещается по некоторой кривой
x( ) . Тогда равенство (1.9) принимает вид
F & x& Fx& t 0 0 .
Полученное равенство называется условием трансверсальности.
Замечание. Условию трансверсальности часто удается придать простой геометрический смысл: например, для функционалов вида
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
h(t, x) |
1 |
2 |
|
|
|
, |
|
|
|
(1.10) |
|||
|
|
x& dt |
|
|
|
||||||||||
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
где функция h(t, x) 0 , имеем: |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
h(t, x) x& |
|
&& |
|
||||||||
|
2 |
|
|
|
|||||||||||
F & |
|
& x& |
h(t, x) 1 x |
|
|||||||||||
x& Fx& h(t, x) 1 x& |
|
|
|
|
|
|
|
|
|
|
. |
||||
|
|
|
|
|
|
|
|
|
|
||||||
1 |
2 |
|
|
2 |
|
||||||||||
|
|
|
|
x& |
|
1 x& |
|
||||||||
Отсюда следует, что условие трансверсальности эквивалентно требованию
1 x&&t 0 0 ,
