
книги / Начала инженерного творчества
..pdf
|
|
|
|
|
|
Таблица 21 |
|
|
|
|
|
|
|
|
|
Поставщики |
|
Потребители |
|
Запас |
|
Штраф |
|
А |
B |
C |
D |
|
|||
1 |
12 |
13 |
4 |
6 |
0 |
|
6 |
200 |
300 |
|
|||||
|
|
|
|
|
|
||
2 |
6 |
4 |
10 |
11 |
700 |
|
2 |
3 |
10 |
9 |
12 |
4 |
800 |
|
5 |
Спрос |
400 |
900 |
0 |
200 |
∑ = 2000 |
|
|
Штраф |
4 |
5 |
0 |
7 |
|
|
|
Снова находится наибольшее значение штрафа (колонка D); в клетку 3D заносится 200 (почему?) и в дальнейшем исключается из рассмотрения колонка D, так как спрос завода D удовлетворен. Запас поставщика 3 уменьшается на 200 и становится равным 800 – 200 = 600.
Продолжая этот процесс, окончательно получаем табл. 22 (проделайте самостоятельно).
|
|
|
|
|
Таблица 22 |
|
|
|
|
|
|
|
|
Поставщики |
|
Потребители |
|
|
Запас |
|
А |
В |
С |
D |
|
||
|
|
|
||||
|
12 |
13 |
4 |
6 |
|
|
1 |
|
|
200 |
300 |
|
0 |
|
6 |
4 |
10 |
11 |
|
|
2 |
|
700 |
|
|
|
0 |
|
|
|
|
|
|
|
|
10 |
9 |
12 |
4 |
|
|
3 |
400 |
200 |
|
200 |
|
0 |
|
|
|
|
|
|
|
Спрос |
0 |
0 |
0 |
0 |
|
|
В результате получился первоначальный опорный план данной задачи:
x1C = 200; x1D = 300; x2B = 700; x3A = 400; x3B = 200; x3D = 200.
101
Все остальные хij = 0. Подсчитаем суммарные затраты:
Z= 4(200) +6(300) + 4(700) +10(400) +9(200) + 4(200) =12 000.
Алгоритм метода Фогеля
1.Для каждого ряда и каждого столбца находим штрафные затраты путем вычитания наименьшей цены из следующей наименьшей цены.
2.Определяем ряд или столбец, где штрафные затраты наибольшие.
3.В выбранном в пункте 2 ряду или столбце максимально заполняем клетку с наименьшей стоимостью.
4.Возвращаемся к пункту 1, при этом ряд или столбец, выбранный в пункте 2, не учитывается.
5.Процесс повторяется до тех пор, пока все потребности не будут удовлетворены и все запасы не будут использованы.
Более подробно методы улучшения решения транспортной задачи см. в учебном пособии [11].
Пример решения транспортной задачи [21]
Необходимо ежедневно с первого склада перевозить в два магазина 50 телевизоров, а со второго склада – 70. При этом первый магазин продает в день 40 телевизоров, а второй – 80
(50 + 70 − 40). В транспортной задаче неравенства в ограничениях заменены равенствами. Получается система линейных алгебраических уравнений с множеством решений, одно из которых оптимизирует целевую функцию. Известны затраты на перевозку одного телевизора со складов в магазины (четыре константы: 1200 руб. при перевозке одного телевизора с первого склада в первый магазин, 1600 руб. – с первого склада во второй магазин, 800 руб. – со второго склада в первый магазин и 1000 руб. – со второго склада во второй магазин).
Программа решения этой задачи в системе MathСAD представлена на рис. 21.
102
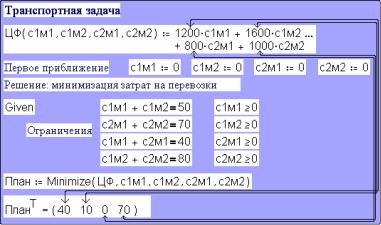
Рис. 21. Решение транспортной задачи в MathCAD
Задание
Сформулируйте и решите задачу о перевозке товара
с3 складов на 4 завода.
2.2.6.Задача о назначениях
Вданном подразделе приведено решение частного случая транспортной задачи – задачи о назначениях. В общем случае смысл задачи о назначениях заключается в следующем: как наилучшим способом назначить n исполнителей для решения n различных задач. Исходя из постановки указанная задача относится к технологическому менеджменту.
Считается, что квалификация каждого исполнителя позволяет выполнить практически любой вид работ, с различной производительностью (или за разное время, с разными затратами и т.д.), и каждый исполнитель может быть назначен для выполнения одной конкретной работы.
Цель назначений зависит от реальной ситуации. Это могут быть наименьшие общие затраты, наименьшее общее время выполнения всех работ, получение наибольшей прибыли и т.д.
103
2.2.6.1. Постановка задачи о назначениях
Пусть Сij – характеристика выполнения i-м исполнителем j-го вида работы (i = 1, 2, ..., n; j = 1, 2, …, m). Обозначим через хij – тип назначения i-го исполнителя на j-ю работу. Очевидно, что величина х может принимать только два значения: хij = 1, если i-й исполнитель назначен на j-ю работу и хij = 0, если i-й исполнитель не назначен на j-ю работу.
Тогда функция
n m |
|
Z = ∑∑Cij xij |
(2.53) |
i=1 j=1 |
|
характеризует выполнение всех видов работ (общая производительность, общее время, суммарные затраты и т.д.). Очевидно, что функция Z есть не что иное, как целевая функция.
Поскольку на каждый вид работы может быть назначен только один рабочий, то
∑ xij = 1, i = 1, 2, ….. n. |
(2.54) |
j =1 |
|
Итак, задача о назначении формулируется следующим образом: определить переменные хij (i = 1, 2, ..., n; j = 1, 2, ..., m) таким образом, чтобы функция
Z = ∑∑Cij xij |
(2.55) |
i =1 j =1 |
|
принимала бы наименьшее (или наибольшее) значение при выполнении условий
∑ xij =1, |
j = 1, 2, ….. n, |
(2.56) |
i=1 |
|
|
∑ xij = 1, |
i = 1, 2, ….. m, |
(2.57) |
j =1 |
|
|
хij = 0 или хij = 1. |
(2.58) |
|
104
По существу, данная задача является транспортной задачей, но со специфичными ограничениями и значениями переменных. Обратим внимание на тот факт, что любой опорный план данной задачи будет вырожденным, так как только n переменных будут не равными нулю.
Конечно, задача о назначении (2.53)–(2.56) может быть решена симплекс-методом или любым алгоритмом решения транспортных задач. Но ее специфичность позволяет использовать специальный алгоритм, который носит название венгерского метода, и сразу же получить оптимальное решение.
2.2.6.2. Алгоритм решения задачи о назначениях «венгерским методом»
Рассмотрим особенности данного метода на конкретном примере. Предположим, что 4 рабочих требуется закрепить за 4 станками таким образом, чтобы суммарное время изготовления деталей было бы минимальным. Известно время, за которое каждый рабочий изготавливает деталь на каждом станке. Эти данные приведены в следующей табл. 23.
|
|
|
|
|
Таблица 23 |
|
|
|
|
|
|
|
|
Исполнители |
|
|
Задача |
|
|
|
1 |
2 |
|
3 |
|
4 |
|
|
|
|
||||
|
|
|
|
|
|
|
1 |
48 |
20 |
|
42 |
|
22 |
|
|
|
|
|
|
|
2 |
28 |
44 |
|
20 |
|
30 |
|
|
|
|
|
|
|
3 |
30 |
34 |
|
40 |
|
38 |
|
|
|
|
|
|
|
4 |
22 |
38 |
|
28 |
|
26 |
|
|
|
|
|
|
|
Из приведенных данных следует, что первый рабочий изготавливает деталь на 3-м станке за 42 мин., третий рабочий тратит 34 мин. на изготовление детали на втором станке и т.д.
Суть «венгерского метода» заключается в последовательном преобразовании исходной матрицы, чтобы добиться необходимого числа нулей.
105
Алгоритм состоит из следующих этапов:
1. Создается новая матрица путем вычитания из каждого элемента каждой строки наименьшего элемента этой строки.
Вприведенном примере необходимо из всех элементов:
–первой строки вычесть 20,
–второй строки вычесть 20,
–третьей строки вычесть 30,
–четвёртой строки вычесть 22.
Врезультате таблица будет иметь следующий вид (табл. 24).
|
|
|
|
|
Таблица 24 |
|
|
|
|
|
|
|
|
Исполнители |
|
|
Задача |
|
|
|
1 |
2 |
|
3 |
|
4 |
|
|
|
|
||||
|
|
|
|
|
|
|
1 |
28 |
0 |
|
22 |
|
2 |
|
|
|
|
|
|
|
2 |
8 |
24 |
|
0 |
|
10 |
|
|
|
|
|
|
|
3 |
0 |
4 |
|
10 |
|
8 |
|
|
|
|
|
|
|
4 |
0 |
16 |
|
6 |
|
4 |
|
|
|
|
|
|
|
2. Снова создается следующая матрица путем вычитания из всех элементов каждого столбца наименьшего элемента этого столбца. Заметим, что в некоторых столбцах после первого этапа есть нули. Естественно, нуль и будет наименьшим элементом, поэтому такие столбцы останутся неизменными. В примере изменится только четвертый столбец (табл. 25).
|
|
|
|
|
Таблица 25 |
|
|
|
|
|
|
|
|
Исполнители |
|
|
Задача |
|
|
|
1 |
2 |
|
3 |
|
4 |
|
|
|
|
||||
|
|
|
|
|
|
|
1 |
28 |
0 |
|
22 |
|
0 |
|
|
|
|
|
|
|
2 |
8 |
24 |
|
0 |
|
8 |
|
|
|
|
|
|
|
3 |
0 |
4 |
|
10 |
|
6 |
|
|
|
|
|
|
|
4 |
0 |
16 |
|
6 |
|
2 |
|
|
|
|
|
|
|
106
3.Определяется наименьшее число горизонтальных (по рядам) и вертикальных (по столбцам) прямых, которыми можно зачеркнуть все нули последней матрицы. Заметим, что в результате выполнения первых двух этапов каждая строка и каждый столбец будут содержать по крайней мере один нулевой элемент. Конечно, все нули возможно зачеркнуть с помощью прямых, совпадающих с каждым рядом (или столбцом), но их количество должно быть наименьшим. Здесь возможны два варианта:
а) наименьшее число таких прямых равно размерности матрицы;
б) число прямых меньше размерности матрицы.
Если число таких прямых равно размерности матрицы, то переходим на этап 5.
Если число прямых меньше размерности матрицы, то переходим на этап 4.
В рассмотренном примере (см. табл. 25) все нули можно зачеркнуть тремя прямыми, проведенными по первой, второй строкам и первому столбцу, но 3 < 4, что говорит о том, что нужно перейти к этапу 4.
4.Среди всех незачеркнутых такими прямыми элементов
втаблице выбирается наименьший и вычитается из остальных незачеркнутых элементов. В результате получается по крайней мере один незачеркнутый ноль, т.е. нужно добавить минимум еще одну прямую, чтобы зачеркнуть все нули. В нашем примере наименьший из незачеркнутых на этапе 3 элемент находится
вклетке (4, 4) и равен 2. Вычитаем 2 из элементов третьей и четвертой строк, за исключением первого столбца. Напомним, что элементы первой, второй строк и первого столбца были зачеркнуты на этапе 3. Получим (табл. 26).
Зачеркнуть все нули возможно только четырьмя прямыми. Число 4 равно размерности матрицы, значит, пора переходить на этап 5.
107
|
|
|
|
|
Таблица 26 |
|
|
|
|
|
|
|
|
Исполнители |
|
|
Задача |
|
|
|
1 |
2 |
|
3 |
|
4 |
|
|
|
|
||||
1 |
28 |
0 |
|
22 |
|
0 |
2 |
8 |
24 |
|
0 |
|
8 |
3 |
0 |
2 |
|
8 |
|
4 |
4 |
0 |
16 |
|
4 |
|
0 |
Замечание. Если бы наименьшее число прямых снова оказалось бы меньше размерности матрицы, то этап 4 пришлось бы повторять до тех пор, пока число прямых стало бы равным размерности матрицы.
5. На этом этапе мы получаем оптимальное решение. Вы уже интуитивно чувствуете, что нужно рассматривать нулевые элементы – и вы абсолютно правы. Вспомним, что каждый рабочий должен быть закреплен только за одним станком. Согласно табл. 26, это значит, что мы должны выбирать одну и только одну клетку в каждом ряду и каждом столбце. Как это сделать? Рассматриваются, как мы уже отмечали, только нулевые клетки. Выбирается такая нулевая клетка, которая является единственной в данном ряду или столбце и помечается знаком X. В табл. 26 клетки (4, 1), (1, 4), (4, 4) не могут быть выбраны, так как эти нули не являются единственными ни в ряду, ни в столбце. Первая нулевая клетка, которая помечается – это (2, 3). Затем помечается клетка (1, 2). Это значит, что мы уже выбрали первый и второй ряды, а также второй и третий столбцы. Иными словами, мы произвели назначение первого рабочего (первый ряд) и второго рабочего на второй и третий станки соответственно. Первый ряд уже выбран, и нулевая клетка (1, 4) больше уже не рассматривается. Следовательно, нулевая клетка (4, 4) стали единственной в четвертом столбце. Пометим ее. В результате ряд 4 не рассматривается, и нулевая клетка (4, 1) «уже не участвует в игре». В первом столбце
108
осталась клетка (3, 1). Заметим, что эта клетка может быть сразу помечена, будучи единственной нулевой клеткой в третьей строке. Назначения произведены следующим образом (табл. 27).
|
|
|
|
|
Таблица 27 |
|
|
|
|
|
|
|
|
Исполнители |
|
|
Задача |
|
|
|
1 |
2 |
|
3 |
|
4 |
|
|
|
|
||||
|
|
|
|
|
|
|
1 |
28 |
X |
|
22 |
|
0 |
|
|
|
|
|
|
|
2 |
8 |
24 |
|
X |
|
8 |
|
|
|
|
|
|
|
3 |
X |
4 |
|
8 |
|
4 |
|
|
|
|
|
|
|
4 |
0 |
14 |
|
4 |
|
X |
|
|
|
|
|
|
|
Первый рабочий закреплен за вторым станком, второй – за третьим, третий – за первым и четвертый – за четвертым. Это и есть оптимальное решение:
х12 = х23 = х31 = х44 = 1.
Все остальные хij = 0. Подсчитаем найденное минимальное значение целевой функции (см. табл. 27):
min Z = 20 + 20 + 26 + 30 = 96.
А теперь подсчитаем общее количество, вычтенное на этапах 1, 2, 4. На этапе 1 вычтено 20 + 20 + 30 + 22 = 92. На этапе 2 и 4 мы вычитали по 2. Общее количество вычтенного равно 96, т.е. равно минимальному значению целевой функции.
Итак, венгерский метод позволяет достаточно просто находить решение задачи о назначениях, при этом используются только арифметические действия сложения и вычитания.
Задача о назначениях, как частный случай транспортной задачи, может иметь особенности, некоторые из которых рассмотрены ниже.
109

Случаи, когда число претендентов не равно количеству мест.
Возможны случаи, когда число исполнителей, которых надо распределить на соответствующую работу, меньше (или больше) количества выполняемых работ (мест). В этом случае вводятся дополнительные фиктивные исполнители (или рабочие места).
Представим, что один исполнитель, например 4, уволился. Тогда необходимо расставить трех исполнителей, имея четыре вакансии. При этом, конечно, общая цель назначений остается неизменной. Введем условно фиктивного исполнителя, характеристики которого будут нулевые, т.е. все характеристики выполнения
C4j = 0 (j = 1, 2, 3, 4).
Получается таблица (табл. 28).
|
|
|
|
|
Таблица 28 |
|
|
|
|
|
|
|
|
Исполнители |
|
|
Задача |
|
|
|
1 |
2 |
|
3 |
|
4 |
|
|
|
|
||||
|
|
|
|
|
|
|
1 |
48 |
20 |
|
42 |
|
22 |
|
|
|
|
|
|
|
2 |
28 |
44 |
|
20 |
|
30 |
|
|
|
|
|
|
|
3 |
30 |
34 |
|
40 |
|
38 |
|
|
|
|
|
|
|
4 |
0 |
0 |
|
0 |
|
0 |
|
|
|
|
|
|
|
Данная проблема решается так же, как и в общем случае, только не нужен этап 2. Оптимальное решение будет следующее:
х12 = х23 = х31 = х44 = 1.
Четвертый станок оказался незанятым. А теперь представим ситуацию, когда число рабочих больше числа станков. Это свидетельствует о том, что один рабочий не будет иметь места. Как произвести назначение в этом случае и кого надо уволить, если цель остается неизменной? Для разрешения этой ситуации
110
