Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Пермский национальный исследовательский политехнический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

книги / Решение электротехнических задач методом конечных элементов

..pdf

Скачиваний:

Добавлен:

12.11.2023

Размер:

944.52 Кб

Скачать

☆

<<< < Предыдущая 1 2 34 / 64 5 6 > Следующая >>>

Окончание табл. 4.1

Номер	1 ,	2 ,	3 ,	4 ,	,		t0	, °С
варианта	Вт/(м·°С)	Вт/(м·°С)	Вт/(м·°С)	Вт/(м·°С)	2	·°С)	t0	, °С
варианта	Вт/(м·°С)	Вт/(м·°С)	Вт/(м·°С)	Вт/(м·°С)	Вт/(м	·°С)
9	384	0,15	0,1	0,2	15			22
10	204	0,3	0,1	0,2	16			21
11	384	0,2	0,1	0,2	17			20
12	204	0,15	0,1	0,2	18			19
13	384	0,3	0,1	0,2	19			18
14	204	0,2	0,1	0,2	20			17
15	384	0,15	0,1	0,2	21			16
16	204	0,3	0,1	0,2	22			15
17	384	0,2	0,1	0,2	15			22
18	204	0,15	0,1	0,2	16			21
19	384	0,3	0,1	0,2	17			20
20	204	0,2	0,1	0,2	18			19
21	384	0,15	0,1	0,2	19			18
22	204	0,3	0,1	0,2	20			17
23	384	0,2	0,1	0,2	21			16
24	204	0,15	0,1	0,2	22			15

Таблица 4.2

Электрические удельные сопротивления и температурные коэффициенты проводниковых материалов

Материал	Удельное сопротивление при	Температурный коэффициент
	20 С ( ρ20 ), Ом м	при 20 С ( αT ), 1/ С
Медь	1,7241 10–8	3,93 10–3
Алюминий	2,8264 10–8	4,03 10–3

Содержание отчета:

1.Титульный лист.

2.Задание.

3.Постановка задачи.

4.Значения токов и сопротивлений ТПЖ.

5.Объемная картинка температурного поля.

6.График температуры поверхности кабеля по окружной координате.

7.Выводы.

5. Двухмерная задача электростатики

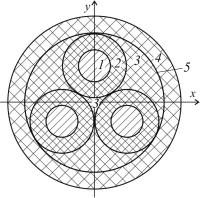
Рассмотрим двухмерную задачу определения электрического потенциала многожильного экранированного кабеля. На рис. 5.1 приведена область исследования трехжильного кабеля. Двухмерное дифференциальное уравнение Лапласа в декартовой системе координат, описывающее распределение электрического потенциала, имеет вид [5]

					0,	(5.1)


	x	x	y	y
где – электрический потенциал;				– относительная диэлектриче-
ская проницаемость.

Рис. 5.1. Трехжильный кабель: 1 – токопроводящая жила (ТПЖ); 2 – изоляция; 3 – межфазное заполнение; 4 – полимерная оболочка; 5 – металлический экран

Дифференциальное уравнение (5.1) дополним граничными условиями: к токопроводящим жилам приложены заданные значения потенциалов. Примем, что на внутренней поверхности оболочки задан потенциал, равный нулю (см. рис. 5.1).

Применение метода Галёркина к уравнению (5.1) даст

T		u		u
N				dV 0,

V	x	x	y	y

где u – приближенное решение.

В результате преобразований уравнения (5.2) получим

	N T	u	N T u		dS 0.
	x		y	y
		x
S

Искомая функция u определяется соотношением u N U .

Тогда

(5.2)

(5.3)

(5.4)

U и

N U

U .(5.5)

Уравнение (5.3) сучетомвыражений(5.4) и (5.5) запишется как

	N T	N	N	T	N
						dS U 0.	(5.6)
	x	x	y		y	dS U 0.	(5.6)
	x	x	y		y
S

Интерполяционный полином для двухмерного симплексэлемента имеет вид [2, 3]

u NiUi

N jU j

NkUk N U ,

ai X jYk XkYj ;

где Ni

ai bi x ci y ;

b Y

Y ;

или N

2S(e)

c X

XkYi XiYk ;

N j

aj bj x cj y ;

Yi ;

или N

2S(e)

(5.7)

X j

;

2S(e)

;

2S(e)

ak XiYj

X jYi ;

b x c y ;

или

;

2S(e)

X j Xi ,

Здесь S(e)

– площадь треугольного симплекс-элемента,

S(e) 1

X j

Тогда матрица градиентов для треугольного симплекс-эле- мента запишется следующим образом:

					Ni	N j

					x	x
	x		N j
B		Ni		Nk	Ni	N j

	y
					y	y

NkxNky

1		bi	bj	bk
			cj
2S	(e)
		ci		ck

1 Yj Yk			Yk Yi	Yi Yj
			Xi Xk		.
2S	(e)
		Xk X j		X j Xi

Уравнение (5.6) с учетом (5.8) примет вид

B T B dS U 0.

(5.8)

(5.9)

Переход от интегрирования по всей области к сумме интегралов по конечным элементам даст

(e) k (e) U 0 ,	(5.10)
(e)

где k (e) B (e)T B (e) dS – локальная матрица коэффициентов.

S( e )

Локальная матрица коэффициентов в (5.10) определится следующим образом:

k (e) B T B dS B T B dS B T B S(e)

S( e ) S(e )

1bibi cici

4S(e) bjbi cjcibk bi ck ci

bibj cicj bjbj cj cj bk bj ck cj

bibk	cick
b b	c c	.	(5.11)
j k	j k
b b	c c
k k	k k

Задание

Дан трехжильный экранированный кабель (рис. 5.1). К токопроводящим жилам приложены заданные значения потенциалов, а к экрану – потенциал, равный нулю.

Найти распределение потенциала в поперчном сечении кабеля. Варианты заданий представлены в табл. 5.1, где относительная диэлектрическая проницаемость изоляции обозначена 2 , а межфаз-

ного заполнения – 3 .

Геометрические параметры расчетной области и разбиение ее на конечные элементы даны в электронной таблице.

						Таблица 5.1
		Варианты заданий

Номер варианта	2		3	U1 , кВ	U2 , кВ		U3 , кВ
1	4,0		1,5	0,00	2,12		–2,12
2	2,2		1,5	0,61	1,75		–2,36
3	4,0		1,5	1,18	1,27		–2,45
4	2,2		1,5	1,68	0,71		–2,38
5	4,0		1,5	2,07	0,10		–2,17
6	2,2		1,5	2,33	–0,51		–1,82
7	4,0		1,5	2,44	–1,09		–1,36
8	2,2		1,5	2,41	–1,60		–0,81
						35

Окончание табл. 5.1

Номер варианта	2	3	U1 , кВ	U2 , кВ	U3 , кВ
9	4,0	1,5	2,22	–2,01	–0,20
10	2,2	1,5	1,89	–2,30	0,41
11	4,0	1,5	1,44	–2,44	1,00
12	2,2	1,5	0,90	–2,42	1,52
13	4,0	1,5	0,31	–2,26	1,95
14	2,2	1,5	–0,31	–1,95	2,26
15	4,0	1,5	–0,90	–1,52	2,42
16	2,2	1,5	–1,44	–1,00	2,44
17	4,0	1,5	–1,89	–0,41	2,30
18	2,2	1,5	–2,22	0,20	2,01
19	4,0	1,5	–2,41	0,81	1,60
20	2,2	1,5	–2,44	1,36	1,09
21	4,0	1,5	–2,33	1,82	0,51
22	2,2	1,5	–2,07	2,17	–0,10
23	4,0	1,5	–1,68	2,38	–0,71
24	2,2	1,5	–1,18	2,45	–1,27

Содержание отчета:

1.Титульный лист.

2.Задание.

3.Постановка задачи.

4.Объемная картинка распределения потенциала.

5.Максимальноезначение напряженностиэлектрическогополя.

6.Код программы.

7.Выводы.

6. Одномерная осесимметричная задача по определению магнитного потенциала при переменном токе

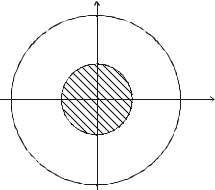
Рассмотрим магнитодинамическую задачу определения магнитного поля одиночного проводника (рис. 6.1). Примем, что ток, протекающий по проводнику, изменяется во времени по косинусоидальному закону. Метод комплексных амплитуд в этом случае позволяет решать задачу как квазистатическую. Тогда уравнение для магнитного потенциала в одномерной осесимметричной постановке запишется как [5, 8]

1 d
1 d	r dA		a J 0,	(6.1)
	r dA		a J 0,	(6.1)
r dr		dr

где A – комплексная амплитуда магнитного потенциала, В с/м; J – комплексная амплитуда плотности тока в проводнике, А/м2; a –

абсолютная магнитная проницаемость, Гн/м, a 0 .

0	RC	R0	r
Рис. 6.1. Поперечное сечение
одиночного проводника

Плотность тока в проводнике определяется по формуле [8]

J Je Js i A Js ,	(6.2)
	37

где Js – плотность тока, определяемая законом Ома в дифференциальной форме (величина Js в пределах одного проводника есть величина постоянная); Je – вихревая плотность тока, Je i A;

– удельная электропроводность, 1/(Ом·м); – круговая частота, рад/с; i – мнимая единица.

С учетом (6.2) уравнение (6.1) запишется как
	d
1		r dA		i a A a Js 0.	(6.3)

r dr			dr

Уравнение (6.3) необходимо дополнить уравнением для заданной величины тока в проводнике. Заданный ток в проводнике определяется по формуле

I	J dS i A Js dS,	(6.4)
SC	SC

где SC – площадь поперечного сечения проводника. Введем новую переменную G [8],

				G	Js	.	(6.5)
				G		.	(6.5)
					i
Тогда
1 d
1 d		r dA		i a A i aG 0;			(6.6)
		r dA		i a A i aG 0;			(6.6)
r dr			dr
	i a A i aG ds a I.						(6.7)
	SC

Дифференциальное уравнение (6.6) дополним граничными условиями:

	0 при r 0;
dA	0 при r 0;	(6.8)
dr		(6.8)

A 0 при r .

Из решения уравнений (6.6), (6.7) с учетом граничных условий (6.8) вычисляются распределение комплексной амплитуды магнит-

ного потенциала A и комплексная величина G , с помощью которой определяется плотность тока Js i G . После этого находится рас-

пределение

плотности

тока

проводнике

из

выражения

J Js i A .

Алгебраическая форма записи величин A ,

и I

имеет вид

;

(6.9)

A A

G G

; I

Здесь индекс

указывает на реальную часть комплексного

числа; индекс I

– на мнимую.

После подстановки выражений (6.9) в уравнения (6.6), (6.7)

и разделения реальной и мнимой частей получим:

1 d

r dA

a AI aGI

(6.10)

r dr

a AR

r dA

aGR

(6.11)

r dr

a AI aGI ds a I R ;

(6.12)

a AR aGR ds a I I .

(6.13)

В результате применения метода Галёркина к уравнениям

(6.10) и (6.11) запишем:

T 1 d

duR

a g

dV 0;

(6.14)

r dr

1 d

duI

a g

dV 0,

(6.15)

r dr

где uR , uI ,

gR ,

g I – приближенные решения.

Искомые величины uR , uI определяются соотношениями:

uR N U R ; uI N U I , (6.16)

							N –
где	U R		и	U I		– вектор-столбцы узловых неизвестных;	N –

матрица функций формы.

Производные по радиусу находятся следующим образом:

d N

;

. (6.17)

Матрицы функции формы и градиентов одномерного сим- плекс-элемента определяются выражениями (2.7) и (2.9).

В пределах одного проводника gR и g I являются постоянными величинами.

Врезультате преобразований уравнений (6.14), (6.15), (6.12)

и(6.13) получим:

R0 B T B rdr U R RC a N T N rdr U I

a N T rdr gI N T N U R R0 0;

RC a N T N rdr U R R0 B T B rdr U I

N T rdr gR

N T N

U I

N rdr U I

2 gI a

I R ;

a I I .

2 gR

N rdr U R

(6.18)

(6.19)

(6.20)

(6.21)

<<< < Предыдущая 1 2 34 / 64 5 6 > Следующая >>>

Соседние файлы в папке книги

#
12.11.202312.71 Mб3Решение некоторых многоэкстремальных задач методом сужающихся окрестностей..pdf
#
12.11.202321.38 Mб4Решение нелинейных задач теории оболочек на ЭВМ..pdf
#
19.11.202332.73 Mб17Решение практических задач при бурении и освоении скважин..pdf
#
12.11.202312.02 Mб0Решение технологических проблем действующего производства средствами автоматизации. Производство калийных удобрений.pdf
#
12.11.20235.01 Mб1Решение частных задач оптимизации для инженерных систем зданий..pdf
#
12.11.2023944.52 Кб1Решение электротехнических задач методом конечных элементов..pdf
#
12.11.2023963 Кб6Риторика и ораторское искусство..pdf
#
12.11.20238.54 Mб1Робот. Компьютер. Гибкое производство.pdf
#
19.11.202351.95 Mб0Рок в Союзе 60-е, 70-е, 80-е..pdf
#
12.11.202310.45 Mб2Роликовые и дисковые конвейеры и устройства..pdf
#
12.11.20231.53 Mб1Роль фаворитизма в социальном процессе..pdf