книги / Строительная механика машин

2.2. Теория вариационных методов

Первое применение вариационных методов в строительной механике связано с именем Релея, который применил закон сохранения энергии к исследованию колебаний струны, стержня, пластинки. Дальнейшее развитие способа Релея принадлежит Ритцу. Ритц показал, что для приближенного решения задач, сводящихся к отысканию экстремума некоторого определенного интеграла, нет необходимости решать уравнение Эйлера – Лагранжа. Можно использовать прямой путь определения функции.

Метод Ритца состоит в следующем. Если ищется функция прогибов w(x), сообщающая минимум интегралу

J = ∫ f (x, w, w′... )dx,

то, задав функцию w(x) в виде ряда

w(x) = a1ϕ1 (x) + a2ϕ2 (x) +... + anϕn (x),

где ai – неопределенные параметры, а ϕi – подходящие функции,

удовлетворяющие граничным условиям задачи, и подставив этот ряд в выражение интеграла J, мы получим функцию от неизвестных параметров ai , где i = 1, 2, …, n.

Для получения экстремального значения J приравниваются нулю производные от J по каждому из параметров ai и решаются n линейных уравнений:

Метод Ритца применен Тимошенко и для решения задач устойчивости стержней и пластинок. В состоянии безразличного равновесия приращение энергии системы при отклонении ее от устойчивой формы равновесия равно нулю. Можно интеграл J, выражающий полную энергию Э системы, представить суммой двух интегралов:

31

интеграла U = F1 (a1,a2 ,...), выражающего энергию внутренних сил, и интеграла W = −Pкр F2 (а1, а2 ,...) (Ркр – критическая нагрузка, при

которой наступает потеря устойчивости системы), определяющего энергию внешних сил.

Из равенства нулю данного интеграла:

J = F1 (а1,а2 ,...) − Pкр F2 (а1,а2 ,...)= 0,

определяется критическое значение нагрузки:

Pкp = F1 ((а1,а2 ,...)). F2 а1, а2 ,...

Значение неизвестных варьируемых параметров определяется с помощью линейных уравнений, полученных из условий:

где р – интенсивность распределенной внешней нагрузки.

При расчете на устойчивость полная потенциальная энергия сжатой пластинки

32

где Nx, Ny и Nxy – мембранные усилия.

Вметоде Ритца рассматривается потенциальная энергия, при этом не применяется дифференциальное уравнение.

Вотличие от метода Ритца метод Галеркина позволяет приближенно решать непосредственно дифференциальное уравнение. Суть этого метода заключается в следующем. Пусть в некотором интервале (a, b) задача приводится к решению дифференциального уравнения

L(x, w, w′, w′′,...) = 0

при заданных граничных условиях. Для приближенного решения его задаем функцию w(x) в виде ряда

w(x) = a1ϕ1 (x) + a2ϕ2 (x) +... + anϕn (x),

где ϕi – линейно независимые функции, удовлетворяющие всем граничным условиям; ai – независимые параметры.

Неизвестные параметры ai определяем из следующих условий:

представляющих линейные относительно ai уравнения.

Метод Галеркина имеет более общий характер по сравнению с методом Ритца, он может быть применен к любым дифференциальным уравнениям, не связанным с вариационными задачами. Условие (2.9) известно как условие ортогональности.

По методу Треффца функции выбираются так, чтобы они были частными интегралами дифференциального уравнения задачи. Оп-

33

ределять же параметры ai он предлагает из условия, что взятый по

всей области интеграл от квадрата градиента ошибки n-го приближения имеет наименьшее значение. Метод Треффца дает приближение искомой функции снизу, а метод Ритца – сверху. Таким образом, оба метода дают нижний и верхний пределы, между которыми заключается истинное значение функции.

Сущность вариационных методов решения дифференциальных уравнений заключается в том, что функции, удовлетворяющие дифференциальному уравнению при заданных граничных условиях, заменяют приближенным аналитическим выражением, наилучшим образом аппроксимирующим эту функцию, т.е. добиваются, чтобы уклонение от искомого значения функции было наименьшим. При решении этой задачи возникает два вопроса:

1)о выборе формы аппроксимирующей функции;

2)о способе приближения функции.

Наиболее удобной формой выражения аппроксимирующей функции является представление функции в виде ряда

n

w(x, y) = ∑aiϕi (x, y) (i =1, 2,3,..., n),

i=1

где ϕi (x, y) – подходящие функции, наилучшим образом изображающие в совокупности исследуемую функцию; ai – неопределен-

ные постоянные параметры, варьируемые в соответствии с принятым способом приближения.

Различают три способа построения ряда:

1. Выбираем функции ϕi так, чтобы каждая из них удовлетворяла части граничных условий. Дифференциальное уравнение при этом не удовлетворяется. Параметры ai определяем из условия, что

весь ряд в целом наилучшим образом аппроксимирует функцию как внутри области, так и на ее границах.

2. Выбираем ϕi так, чтобы каждая из них в отдельности удовлетворяла всем граничным условиям. Дифференциальное уравнение

34

при этом не удовлетворяется. Параметры ai определяем из условия,

что весь ряд наилучшим образом аппроксимирует функцию внутри области.

3. Выбираем ϕi так, чтобы каждая из них удовлетворяла дифференциальному уравнению, т.е. была частным интегралом этого уравнения. Граничные условия не удовлетворяются. Параметры ai

определяем из условия, чтобы весь ряд наилучшим образом аппроксимировал функцию на концах промежутка.

Первый способ построения проще других, поскольку он налагает на функции ϕi наименьшее число ограничений. Однако условие

для определения параметров оказывается более сложным. В целом же весь ряд должен наиболее близко соответствовать ожидаемому характеру изменения функции. Чем ближе ряд представляет искомую функцию, тем быстрее идет процесс сходимости приближения.

Ниже приводятся некоторые «подходящие» функции прогибов для пластинок при различных условиях закрепления контура:

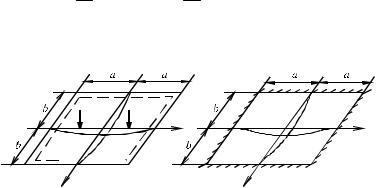
1. Свободное опирание прямоугольной пластинки по контуру (рис. 2.3, а) при симметричном нагружении:

w(x, y) = a1 cos 2πax cos π2by + a2 cos 2πax cos 32πby + a3 cos 32πax cos 32πby +..., w(x, y) = a1 (x2 −a2 )(y2 −b2 )+ a2 (x2 −a2 )x2 (y2 −b2 ) y2 +...

Рис. 2.3. Схема нагружения прямоугольной пластины: а – свободно опертой; б – защемленной по контуру

35

2. Защемление по контуру прямоугольной пластинки при симметричном нагружении (рис. 2.3, б):

w(x, y) = a1 cos2 π2ax cos2 π2by + a2 cos2 32πax cos2 32πby +...,

w(x, y) = a1 (x2 −a2 )2 ( y2 −b2 )2 + a2 (x2 −a2 )2 (y2 −b2 )2 + + a3 (x2 −a2 )2 (y2 −b2 )2 +...,

w(x, y) = a1 (x2 −a2 )2 (y2 −b2 )2 + a2 cos2 π2ax cos2 π2by +

+a3 cos2 32πax cos2 32πby +...

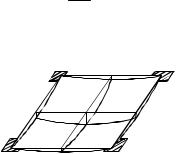
3.Свободное опирание пластинки по углам (рис. 2.4):

w(x, y) = a1 cos π2ax + a2 cos 2πby + a3 cos 32πax + a4 cos 32πby +...,

w(x, y) = a1 (x2 −a2 )+ a2 (y2 −b2 )+ a3 (x2 −a2 )x2 + a4 (x2 −a2 ) y2 +...

Рис. 2.4. Вид прогибов свободно опертой по углам прямоугольной пластины

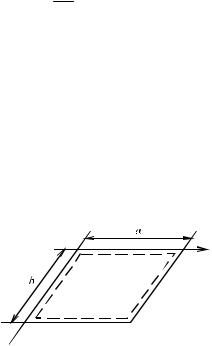
4. Свободное опирание эллиптической пластинки при симметричном нагружении (рис. 2.5):

36

δЭ = ∂Э = 0 (i =1, 2, 3, ..., n).

∂ai

Мы получим n уравнений для определения неизвестных ai ,

разрешив которые получим функцию прогибов (2.10).

Пример 1. Рассмотрим в качестве примера изгиб свободно опертой по контуру прямоугольной пластинки (рис. 2.6) под действием равномерно распределенной внешней нагрузки интенсивностью р. Зададим функции прогибов в виде двойного тригонометрического ряда:

x

y

Рис. 2.6. Прямоугольная пластинка, свободно опертая по контуру

После подстановки данного ряда в выражение полной энергии (2.6), интегрирования и преобразований получим:

Дифференцирование по коэффициентам amn даст нам следующее выражение:

38

Если в формуле (2.12) взять бесконечно большое число членов, то получим решение задачи, совпадающее с точным.

Ограничившись одним членом ряда, имеем для m = 1, n = 1:

Максимальный прогиб возникает в центре пластинки при

39

Для квадратной пластинки (a =b) максимальный прогиб

Для коэффициента Пуассона µ = 0,3 после подстановки выражения цилиндрической жесткости получим:

wmax = 0,0443 pa4 ,

Еh6

т.е. погрешность составляет 2,7 %.

Изгибающие погонные моменты определяются по формулам:

Максимальные изгибающие моменты действуют в центре пла-

Точное значение максимальных изгибающих моментов для квадратной пластинки [3]

Мxmax = Мymax = 0,0479 pa2 .

40