
|
|
|
|
20 |
|
|
|
|
1.2.3. Кинематические параметры |
|
|
|
|
|
|||
1. Перемещение |
|
|
|
|
|
|
|
|
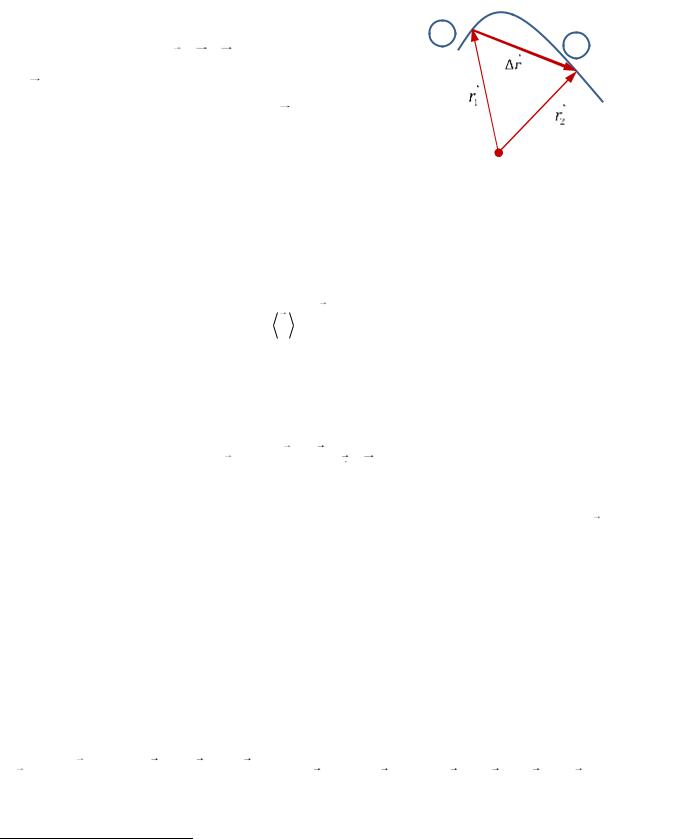
Перемещение (смещение) — приращение радиуса- |
|
1 |
S |
t2 |
||||
вектора |
|
|
|
|
||||
|
|
|
|
|
||||
|
|
|
|
|
t1 |
|
|
|
|
r r |
r |
, |
|
|
2 |
||
|
|
|
|
|
||||
|
2 |
1 |
|
|
|
|
||
где r1 — радиус-вектор материальной точки, соверша- |
|
|
|
|
||||
ющей движение, в момент времени t1, r2 |
— радиус-век- |
|
|
|
|
|||
тор в момент времени t2 (РИС. 1.7); |
|
[r] = м8. |
O |
Путь S — длина участка траектории (1-2 на РИС. 1.7). |
Рис. 1.7 |
r ≠ S! |
|
2. Скорость
Скорость — векторная величина, характеризующая быстроту движения.
Средняя скорость
v |
|
r t
,
где t — промежуток времени; t = t2 – t1 на РИС. 1.7;
|
|
|
v |
|
|
м |
. |
|
|
|
|
с |
|
|
|||||
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
Мгновенная скорость |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
v lim |
|
r |
|
dr |
r r |
|
. |
|
|
|
|
|
|
|||||
|
t 0 |
|
t |
|
|
dt |
t |
||
|
|
|
|
|
|
|
|||
(В этой формуле представлены различные варианты обозначения производной ра-
диуса-вектора по времени. В последующих разделах и главах мы будем писать
и т. п.)
Вектор мгновенной скорости направлен
Средняя путевая скорость
vпут
по касательной к траектории.
|
S |
. |
|
t |
|||
|
|||
|
|
dr dt
В дальнейшем под словом «скорость» мы будем понимать мгновенную скорость, если не оговорено иное.
Выразим вектор мгновенной скорости через проекции на оси декартовой системы координат:
v lim |
r |
lim |
x i |
y j |
z k lim |
x i lim |
y |
j lim |
z k dx i dy |
j dz k; |
||
t 0 |
t |
t 0 |
|
t |
t 0 |
t |
t 0 |
t |
t 0 |
t |
dt dt |
dt |
8 Здесь и далее в конспекте лекций квадратные скобки в подобном контексте означают единицы измерения данной величины в СИ.

21
|
v |
|
|
dx |
, |
|
|
|
|
|
|
|
|
x |
dt |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dy |
|
|
|
|
|
|
dr |
|
|
|
|
|
|
, |
|
2 |
2 |
2 |
; v |
! |
||
vy |
|
v |
|
|||||||||
dt |
vx |
vy vz |
dt |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
dz |
|
|
|
|
|
|
|
|
|
|
v |
|
|
; |
|
|
|
|
|
|
|
|
|
z |
dt |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
Обратная задача
Дано v t , найти r t .
За малое время dt материальная точка совершает перемещение dr мируем все малые перемещения, т. е. проведём интегрирование по
0 |
|
t |
|
. |
|
|
v t dt |
||
r r |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
v dt . Просумвремени:
(1.1)
Здесь
r0
— начальный радиус-вектор, т. е. радиус-вектор движущейся материаль-
ной точки в начальный момент времени.
Выражение (1.1) можно записать и в координатной форме.

22
Лекция 2
1.2.3. Кинематические параметры (продолжение)
3. Ускорение
Ускорение — векторная величина, характеризующая скорость изменения скорости материальной точки.
Среднее ускорение:
a |
|
v t
;
a |
м |
||
с |
2 |
||
|
|||
|
|
||
Мгновенное ускорение:
.
a lim |
v |
dv |
v v |
d2r |
r r |
. |
t 0 |
t |
dt |
t |
dt2 |
t |
|
Мгновенное ускорение в проекциях на оси декартовой системы координат:
|
|
|
dv |
|
|
|
d |
2 |
x |
|
|
|||
|
|
x |
|
|
|
|
, |
|||||||
a |
x |
|
|
|
|
|
2 |
|
||||||
|
|
dt |
|
|
dt |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|||||
|
|
dv |
|
|
d |
2 |
|
y |
|
|||||
|
|
|
y |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
||||
a |
|
|
|
|
|
|
|
|
|
|
|
, |
||
|
y |
|
dt |
|
dt |
2 |
|
|
||||||
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
||
|
|
|
dv |
|
|
|
d |
z |
|
|
||||
|
|
z |
|
|
|
; |
||||||||
a |
z |
|
|
|
|
2 |
||||||||
|
|
dt |
|
|
dt |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|||||
a a |
i a |
y |
x |
|
j az k
.
Обратная задача
Дано a t , найти v t и r t .
|
|
v t v0 t |
a t dt |
, |
r t r0 t |
v t dt r0 v0t t |
dt t |
a t dt |
. |
|
|
|
0 |
|
|
|
0 |
0 |
0 |
|
|
|
|
|
|
|
|
|
||||
Здесь v0 |
— начальная скорость, r0 |
— начальный радиус-вектор. Эти выражения |
||||||||
можно записать и в координатной форме. |
|
|
|
|
||||||
ПРИМЕР РЕШЕНИЯ ОБРАТНОЙ ЗАДАЧИ9
1) Равномерное движение:
v const |
|
|
|
|
|
|
t |
|
|
a 0 ; |
r r0 |
|
vdt r0 |
vt . |
|
||||
|
|
0 |
|
|
9 В этом разделе не приводится пример расчёта скорости, ускорения, модуля радиуса-вектора и т. д. из-за нехватки времени. Простые примеры на эту тему следует рассмотреть на практических занятиях.
23
2) Равноускоренное движение:
0 |
|
t |
|
|
|
|
|
v t v |
|
|
adt |
|
|
0 |
|
a const |
|
|
|
|
|
|
|
|
t |
v0 |
at dt r0 |
|
at |
2 |
|
v0 at ; r r0 |
|
v0t |
|
||||
2 |
|||||||
|
|||||||
|
0 |
|
|
|
|||
|
|
|
|
|
|
||
.
1.2.4. Криволинейное движение |
|
|
||
|
|
|
При описании движения материальной |
|
t1 |
|
|
точки по криволинейной траектории удобно |
|
|
t2 |
ввести систему координат, связанную с тра- |
||
1 |
|
|||
|
|
|
екторией материальной точки (воспользо- |
|
|
|
|
ваться естественным способом |
описания |
|
2 |
|
движения). |
|
|
|
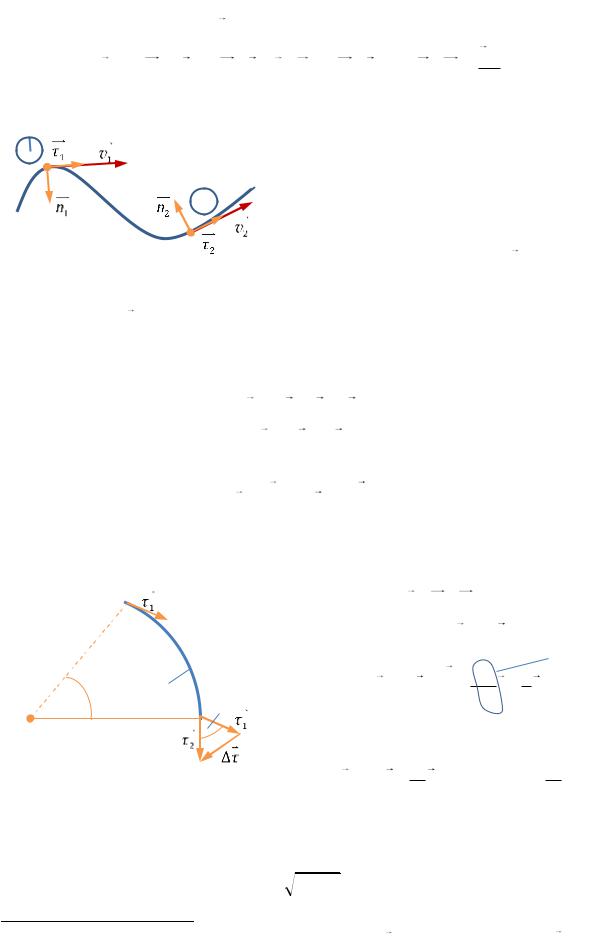
Орты этой системы координат: τ |
— единич- |
|
|
|
|
||
|
Рис. 2.1 |
ный вектор, направленный по касательной к |
||
траектории по направлению движения мате-
риальной точки; n — единичный вектор, направленный по нормали к траектории в сторону её вогнутости (см. РИС. 2.1).
Разложим векторы скорости и ускорения по осям естественной системы координат:
v vτ τ 0n vτ ; a aτ τ an n.
Но, по определению
(2.1)
a |
dv |
|
dt |
||
|
dv τ v dτ dt dt
.
(2.2)
Разберёмся, чему равны слагаемые в формуле (2.2). Любую кривую в любой её точке можно представить как дугу окружности радиуса ρ — радиуса кривизны траектории (РИС. 2.2).
|
ρ |
|
l |
α |
α |
O |
ρ |
|
|
|
Рис. 2.2 |
l ρ |
α ; |
|
τ τ2 τ1 |
, |
|
τ τ |
α |
|
||||||
|
|
τ |
l |
, |
τ |
l |
n 10. |
|
|
|||||
|
ρ |
ρ |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
v |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
При t → 0 |
dτ |
dl |
n, |
dτ |
|
|
dl |
|
n |
v |
n . |
|
||
ρ |
dt |
ρdt |
|
ρ |
|
|||||||||
|
|
|
|
|
|
|
|
|
||||||
Подставляя эти выражения в (2.2) и сравнивая с (2.1), получим
|
dv |
|
|
2 |
|
|
|
|
|
|
|
|
|
2 |
|
|
a |
τ |
v |
n |
; |
a |
|
dv |
, |
a |
|
v |
;(2.3) |
||||
|
|
|||||||||||||||
|
|
|
|
|
|
|||||||||||
|
dt |
|
ρ |
|
τ |
|
dt |
n |
|
ρ |
||||||
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
aτ — тангенциальное (касательное) ускорение, an — нормальное (центростремительное) ускорение;
a 
 aτ2 an2 .
aτ2 an2 .
10 Следует помнить, что на РИС. 2.2 угол α мал. При малом α τ практически параллелен n .

24
1.3. Кинематика твёрдого тела
1.3.1. Виды движения
1.Поступательное движение — движение, при котором любая прямая, соединяющая две точки движущегося тела, перемещается параллельно самой себе.
2.Вращение вокруг неподвижной оси (вращательное движение) — движе-
ние, при котором все точки тела движутся по окружностям, лежащим в параллельных плоскостях, таким, что центры этих окружностей лежат на одной прямой, называемой осью вращения.
3.Плоское движение — движение, при котором все точки тела движутся в параллельных плоскостях.
Плоское движение = поступательное движение + вращательное движение (см. разделы 1.7.1 и 1.8.1).
4.Сферическое движение (вращение вокруг неподвижной точки) — движе-
ние, при котором все точки тела движутся по сферам, центры которых находятся в одной точке, называемой центром вращения.
5.Другие случаи – сложное движение11.
Демонстрации: 1) Поступательное и вращательное движение
2)Искры от точила
3)Циклоида
4)Гироскоп12
Введённых нами ВЫШЕ кинематических величин недостаточно для описания движения твёрдого тела (кроме поступательного).
1.3.2. Угловые кинематические параметры
Введём величины, характеризующие вращательное движение твёрдого тела в целом, а не отдельных его точек. Такие величины будут аксиальными векторами.
|
Векторы |
полярные |
аксиальные |
(истинные) |
(псевдовекторы) |
имеют точку приложения |
не имеют точки приложения |
, , , |
, , , |
(Здесь
F
— сила, p — импульс,
M
— момент силы, L — момент импульса.)
11На практических занятиях рассматривается поступательное движение, вращение вокруг неподвижной оси и плоское движение. Сферическое движение и общий случай сложного движения и в лекционном курсе будут затронуты мало.
12Движение гироскопа демонстрируется не как пример выполнения закона сохранения момента
импульса, а лишь как пример сферического движения твёрдого тела.

25
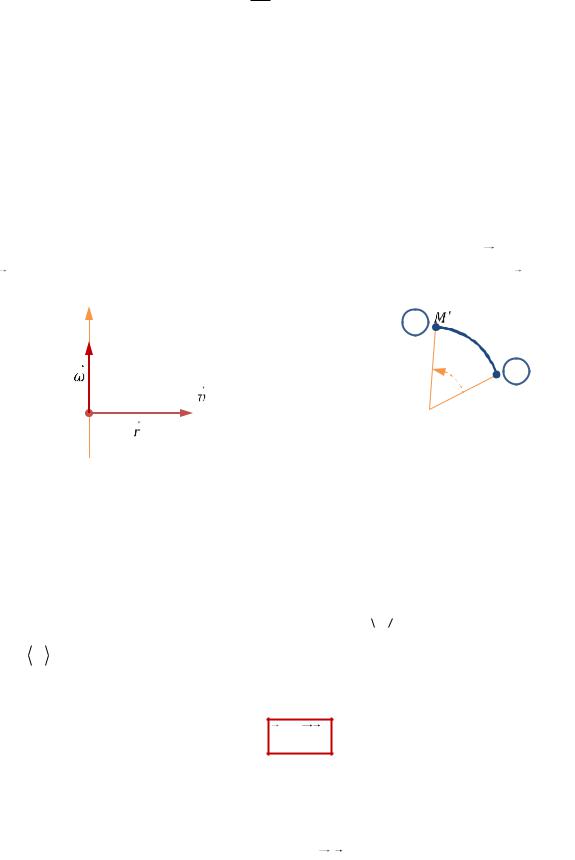
1. Угловое перемещение
z
O
r φ
A
Рис. 2.3
φz 0.
Пусть твёрдое тело вращается вокруг оси z. Точка A этого тела находится на расстоянии r от оси вращения (РИС. 2.3). За некоторое время тело повернулось так, что точка A переместилась по дуге окружности радиуса r в положение A'. При этом отрезок OA (точка O – центр окружности, по которой движется точка A) повернулся на угол φ.
Это движение характеризует вектор углового пере-
мещения |
φ |
k (k — орт оси вращения z). Вектор- |
ная величина |
φ вводится лишь для малых угловых |
|
перемещений. Направление φ выбирается по пра-
вилу правого винта.
Можно записать
φ |
φz k , |
Любой поворот твёрдого тела можно характеризовать скалярной величиной — уг-
лом φ. Можно задать закон вращательного движения твёрдого тела
φz
φz
t
.
Единица измерения углового перемещения в СИ
|
|
[φ] = рад (радиан — безразмерная величина); |
|
1 |
π |
рад . (При проведении численных расчётов следует обращать внима- |
|
180 |
|||
|
|
ние на единицы измерения углового перемещения!)
2. Угловая скорость
Угловая скорость — векторная величина, характеризующая быстроту и направление вращения;
ω |
dφ |
; ω |
рад |
1 |
|
dt |
с |
с . |
|||
|
|||||
|
|
|
|||
|
|
|
|
3. Угловое ускорение
Угловое ускорение — векторная величина, характеризующая быстроту и направление изменения угловой скорости;
|
dω |
|
2 |
φ |
|
|
ε |
|
d |
; |
|||
dt |
dt |
2 |
||||
|
|
|||||
|
|
|
|
|||
При вращении вокруг неподвижной оси
ε φ
рад |
|
с |
2 |
|
|
ω |
|
с |
2 |
. |
|
||
ε |
k |
|
(
k
— орт оси вращения);
знаки проекций этих векторов на ось вращения могут быть различны.
4. Частота вращения
Частота вращения — скалярная положительная величина, характеризующая быстроту вращения, равная числу оборотов тела вокруг оси вращения за единичный промежуток времени;
26
ν |
ω |
|
2π |
||
|
; |
|
ν |
об |
|
с |
||
|
с |
1 |
|
.
5. Период вращения
Период вращения — скалярная положительная величина, характеризующая быстроту вращения, равная времени, за которое вращающееся тело совершает один полный оборот вокруг оси вращения;
T |
1 |
|
2π |
; [T] = с. |
|
ν |
ω |
||||
|
|
||||
|
|
|
Период вводится только при равномерном вращении, т. е. при вращении с постоянной угловой скоростью.
1.3.3. Связь между линейными и угловыми кинематическими параметрами
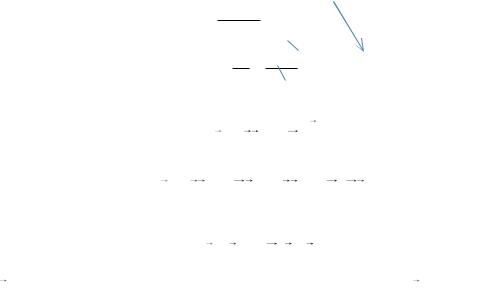
Пусть твёрдое тело вращается вокруг оси z с угловой скоростью ω |
и ускорением |
||||||||
ε . Точка M отстоит от оси вращения на расстояние r; её скорость равна v (РИС. 2.4А). |
|||||||||
z |
|
|
|
|
|
|
S |
|
|
|
t + |
|
t |
|
|
|
t |
||
|
|
|
|
|
|
||||
|
|
|
|
|
φ |
|
M |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
r |
|
|
|
O |
M |
z |
|
|
|
|
|||
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
а |
|
|
|
б |
|
|
|
|
Рис. 2.4
(Значки , на РИС. 2.4 означают направление вектора, перпендикулярного плоскости чертежа, — соответственно «на нас» и «от нас».)
За время t точка M переместилась в положение M |
по дуге длиной S (РИС. 2.4Б). |
Тело за это время совершило угловое перемещение |
φ; |
S r
φ
,
v
S |
|
r |
t |
|
|
|
|
φ t
 ω
ω r
r
,
где |
ω |
— среднее значение модуля угловой скорости за время |
|
|
v ωr , |
а соответствующее векторное равенство
v ωr
t. При t → 0
(2.4)
(направление можно проверить по РИС. 2.4А). Здесь квадратные скобки означают векторное произведение векторов. (Следует помнить о том, что векторное произ-
ведение антикоммутативно!)
Формула (2.4) справедлива и в произвольном случае сложного движения. Тогда v ωr sin ω,r .
27
Выразим компоненты линейного ускорения (т. е. ускорения точки M), воспользовавшись формулой (2.3):
|
aτ |
dv |
|
d ωr |
r |
dω |
ω |
dr |
εzr |
, |
|||||||||||||||||||||||
|
dt |
|
dt |
|
|
dt |
dt |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
v |
2 |
|
|
|
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
||
|
|
|
|
an |
|
|
ω r |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
r |
|
|
r |
|
|
|
ω r . |
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Полное ускорение |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
a |
|
εr |
|
|
|
|
|
|
dr |
, |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
ω |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
dt |
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
a |
|
εr |
|
|
|
|
ωv |
|
|
|
εr |
|
|
|
|
|
|
|
ωr |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
ω |
|
|
. |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Для сложного движения твёрдого тела |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
v vC |
|
|
ω r |
rC |
|
, |
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
где rC |
— радиус-вектор центра масс тела (см. РАЗДЕЛ 1.4.4), |
||||||||||||||||||||||||||||||||
масс. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
vC
(2.5)
— скорость центра
28
Лекция 3
1.4. Динамика материальной точки
Динамика — раздел механики, изучающий влияние взаимодействия тел на механическое движение.
1.4.1. Законы Ньютона
I закон Ньютона: существуют такие системы отсчёта, в которых материальная точка сохраняет состояние покоя или равномерного прямолинейного движения до тех пор, пока воздействие других объектов не выведет её из этого состояния.
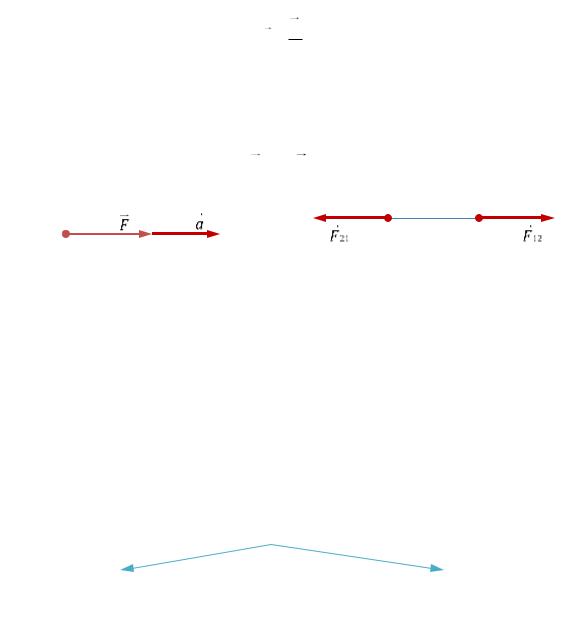
II закон Ньютона: ускорение материальной точки совпадает по направлению с силой, с которой действуют на неё другие тела, и равно отношению этой силы к массе точки:
a |
F |
|
m |
||
|
(см. РИС. 3.1).
III закон Ньютона: две материальные точки действуют друг на друга с силами, равными по модулю, противоположными по направлению и направленными вдоль прямой, соединяющей эти точки:
|
F12 F21 |
|
|
(см. РИС. 3.2). |
|
|
|
m |
1 |
2 |
|
Рис. 3.1 |
|
|
Рис. 3.2 |
Демонстрация: Тележки |
|
|
|
1.4.2. Инерциальные системы отсчёта. Инертность
С точки зрения физики покой и равномерное прямолинейное движение суть одно и то же.
Инерциальная система отсчёта (ИСО) — система отсчёта, относительно которой материальная точка, не испытывающая внешних воздействий, движется равномерно и прямолинейно.
I закон Ньютона можно сформулировать так: инерциальные системы отсчёта существуют.
Примеры систем отсчёта, которые можно считать инерциальными в условии большинства задач:
|
ИСО |
гелиоцентрическая |
лабораторная |
тело отсчёта — Солнце |
тело отсчёта — лаборатория (земля) |
Все тела обладают инертностью — свойством сохранять состояние покоя или равномерного прямолинейного движения в отсутствие внешних воздействий.
29
Масса — скалярная физическая величина — рой его инертности;
|
|
|
|
m |
кг |
характеристика тела, являющаяся ме-
.
1.4.3. Сила
Сила — векторная величина — мера воздействия на данное тело другого объекта. Каждая сила описывает действие какого-либо объекта;
F Н
(ньютон).
Линия действия силы — прямая, вдоль которой направлена сила.
Силовая линия—кривая, касательные к которой в каждой её точке совпадают по направлению с силой.
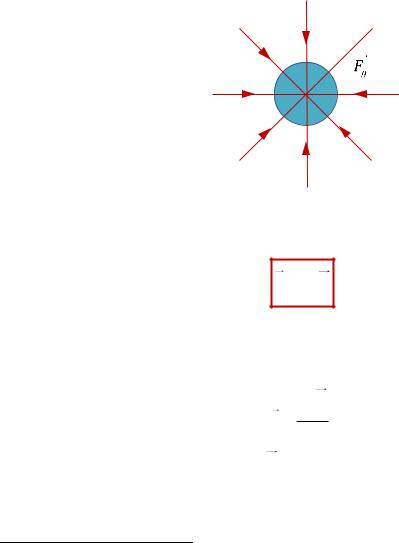
ПРИМЕР
Силовые линии гравитационного поля Земли (РИС. 3.3)
 m
m
O
Рис. 3.3
Главный вектор13 — векторная сумма всех сил, описывающих действие на данное тело других объектов:
n
FFi
i1
(здесь n — число воздействующих объектов).
Принцип независимости действия сил: если на материальную точку одновре-
менно действует n объектов, то ускорение этой точки
где m — масса материальной точки, екта на данную точку.
|
|
n |
|
|
|
i |
|
|
|
F |
|
|
a |
|
|
|
|
i 1 |
, |
|
|
m |
|
|
|
|
|
Fi |
— сила, описывающая воздействие i-го объ- |
||
13 Вводится ещё понятие равнодействующей силы — силы, эквивалентной данной системе сил, т. е. силы, описывающей такое воздействие на данную механическую систему, под которым система будет двигаться так же, как под воздействием всех n объектов. Не для каждой системы сил можно подобрать равнодействующую. Для материальной точки понятия равнодействующей и главного вектора сил эквивалентны.
