Добавил:

PotapkinBY t.me Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный исследовательский университет «МЭИ»

Предмет:

Физика

Файл:

2 семестр / Лекции по физике. Лубенченко

.pdf

Скачиваний:

Добавлен:

16.07.2023

Размер:

7.88 Mб

Скачать

☆

<<< < Предыдущая 2 3 4 5 6 7 8 9 10 11 12 1314 / 4014 15 16 17 18 19 20 21 22 23 24 25 26 > Следующая >>>

130

зависит только от его длины.

2. Физический маятник

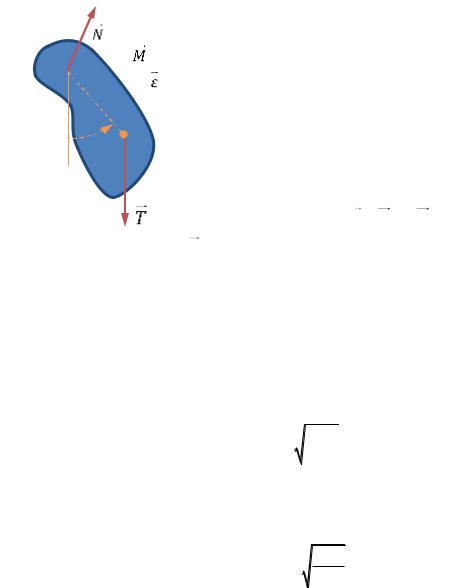
Физический маятник — твёрдое тело, которое может вращаться вокруг неподвижной горизонтальной оси, про-

ходящей через точки этого тела, не являющиеся его цен-

z			тром масс, в однородном гравитационном поле.
			Пусть масса маятника равна m, его момент инерции отно-
	d		Пусть масса маятника равна m, его момент инерции отно-
	d		сительно оси маятника равен I, расстояние между центром
φ		C	сительно оси маятника равен I, расстояние между центром
φ		C	масс маятника и его осью z равно d (РИС. 15.5). Найдём пе-
			масс маятника и его осью z равно d (РИС. 15.5). Найдём пе-
			риод колебаний маятника.

Запишем основное уравнение динамики вращательного движения:

Рис. 15.5

	Iε MF	MN
	т
( N	— сила реакции оси маятника).
нение на ось маятника:

Спроецируем это урав-

	2
I	d φ
I	dt	2
		2

При малых углах φ sin φ ≈ φ и

mgdsinφ

d2φ	mgd φ 0.
dt2		I
Обозначив
ω0		mgd	,
ω0		I	,
		I

получим дифференциальное уравнение свободных гармонических колебаний. Пе-

риод колебаний T0 2π ,

ω0

T 2π	I
T 2π
0	mgd
	mgd

Приведённая длина физического маятника — длина математического маятника с периодом собственных колебаний, равным периоду собственных колебаний данного физического маятника.

Демонстрация: Математический и физический маятники

Из приведённых выше примеров видно, что свободные незатухающие механические колебания будут гармоническими лишь при малых изменениях колеблющейся величины.

131

Лекция 16

1.14.3. Свободные затухающие колебания

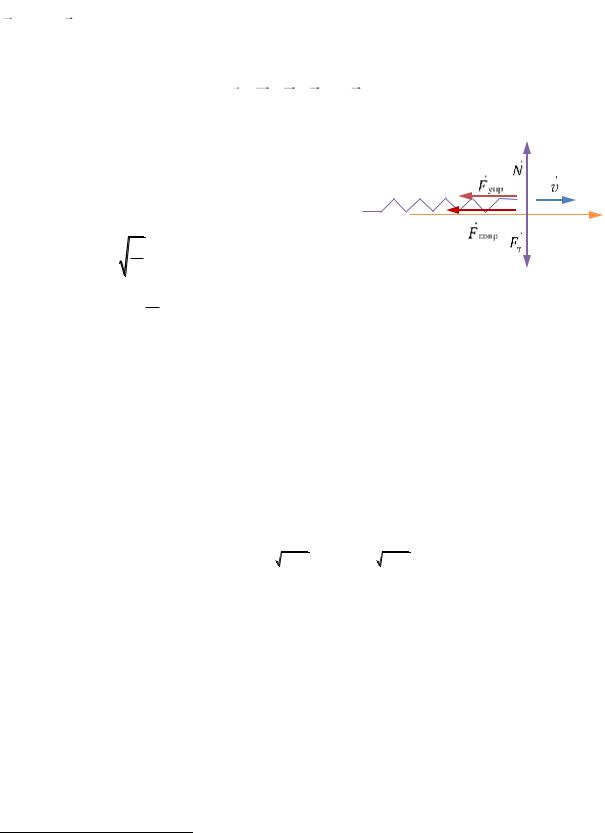
Рассмотрим пружинный маятник (см. 1.14.2), введя силу сопротивления в виде

Fсопр rv

— сила вязкого трения, r — положительная константа. Колебательная

система изображена на РИС. 16.1.

Запишем II закон Ньютона для груза:

ma Fт N F упр

Fсопр

В проекции на ось x

d2x

kx r

dt2

d2x

r dx

dt2

x 0.

Обозначим ω0

Рис. 16.1

2β

β — коэффициент затухания;

2β

ω x 0

(16.1)

— дифференциальное уравнение свободных затухающих колебаний.

Это также однородное дифференциальное уравнение второго порядка с постоянными коэффициентами. Вид его общего решения45 зависит от величины коэффициента затухания.

1. Сильное затухание (β ≥ ω0)

Общее решение дифференциального уравнения (16.1)

			0					0
	β	2	2	t		β	2	2	t
x t A e	β	β	ω	t	A e	β	β	ω	t
x t A e					A e
1					2

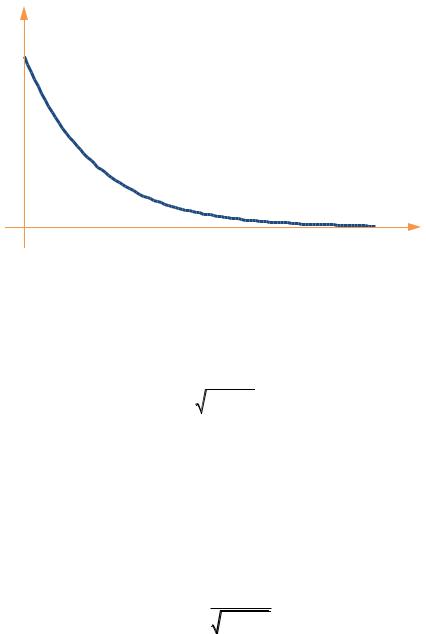
— апериодическое решение, здесь A1 и A2 — постоянные, определяемые из начальных условий. Колебаний нет, имеет место апериодический процесс. Примерный график апериодического процесса показан на РИС. 16.2.

45 Можно провести решение дифференциального уравнения (16.1) через характеристическое уравнение.

132

0	t
	Рис. 16.2

2. Слабое затухание (β < ω0)

Общее решение дифференциального уравнения (16.1)

	x t A e		βt	cos ωt φ		,
	x t A e			cos ωt φ
	0
где

		ω	ω β
				2	2
				0

— циклическая частота затухающих колебаний.

(16.2)

Величины A0 и φ в решении (16.2) — это постоянные, определяемые из начальных условий. Заметим, что затухающие колебания не являются колебаниями в строгом смысле этого слова (см. ОПРЕДЕЛЕНИЕ).

Амплитуда затухающих колебаний

A t A e	βt	;

0

период затухающих колебаний

T	2π	2π
T	ω	ω	β	2
		2		2
		0

С другими характеристиками свободных затухающих колебаний познакомимся во II семестре (РАЗДЕЛ 3.13.2).

График решения (16.2) при φ = 0 показан на РИС. 16.3.

133

Рис. 16.3

Демонстрация: Маятник с песком

1.14.4. Вынужденные колебания

Пусть пружинный маятник — механическая система, описанная в РАЗДЕЛЕ 1.14.2, при наличии сопротивления, находится под воздействием, описываемым периодической силой

F F0 cosΩt ,

Ω — циклическая частота вынуждающей силы. Сила

(РИС. 16.4).

направлена горизонтально

m k

O	x

Рис. 16.4

Запишем II закон Ньютона для груза:

ma F	N F упр Fсопр
т

В проекции на ось x

md2x kx r dx F0 cosΩt , dt2 dt

так как Fупр x = –kx, Fсопр x = –rvx. Получим

d2x	r dx	k		F
dt2			x	0 cosΩt .
	m dt	m
				m

134

Обозначим

k m

ω2 0

	r	2β
	m	2β
	m

			F		f0	;
				0	f0	;
				0
			m

2	x		dx
d	x	2β	dx		2			cosΩt
	2	2β		ω x f			0	cosΩt	(16.3)
dt	2		dt		0		0		(16.3)
dt			dt

— дифференциальное уравнение вынужденных гармонических колебаний.

Это линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентами. Его общее решение — сумма общего решения однородного уравнения (16.1) и частного решения неоднородного уравнения (16.3) (ищем решение при слабом затухании — β < ω0)

x t x1 t x2 t ;
общее решение		частное решение
ОДУ		НДУ
x1 t A1e	βt	cos ωt φ ;

x2 t A2 cos Ωt φ0 .

(16.4)

Здесь

ω	β
2		2
0

; A1 и φ — постоянные интегрирования; A2 и φ0 найдём подста-

новкой решения (16.4) в дифференциальное уравнение (16.3).

Общее решение x1(t) быстро затухает. В результате циклическая частота вынужденных колебаний будет равна циклической частоте Ω вынуждающей силы.

Производные функции x2(t)

dx2 dt

A2Ωsin Ωt

φ0

d	2	x

dt		2

A2Ω2 cos Ωt

φ
0

Подставим эти производные в исходное дифференциальное уравнение (16.3):

2	cos Ωt φ	2βΩA sin Ωt φ		2
Ω A	cos Ωt φ	2βΩA sin Ωt φ		ω A cos Ωt φ
2	0	2	0	0	2	0

f	0	cosΩt
	0

(16.5)

Это равенство должно соблюдаться при любом t, в т. ч. тогда, когда cos (Ωt + φ0) = 0 либо sin (Ωt + φ0) = 0. Преобразуем правую часть уравнения (16.3):

f0 cosΩt f0 cos Ωt φ0	φ0 f0	cos Ωt φ0 cosφ0	sin Ωt φ0	sinφ0	.

Подставим это выражение в (16.5) и приравняем нулю сначала cos (Ωt + φ0), а затем sin (Ωt + φ0):

Ω2 A		ω2 A			f	cosφ ,
	2	0		2	0	0	(16.6)
							(16.6)
2βΩA f				sinφ .
		2	0		0

Разделив нижнее равенство на верхнее, получим

tgφ	2βΩ
	2		2
0		Ω
	ω
	0

Вынужденные колебания отстают по фазе от вынуждающей силы на φ0.

Найдём амплитуду A2 вынужденных колебаний из первого уравнения системы

(16.6):

135

A	f	cosφ		f			1		f			1					f
A	0		0		0					0								0
	0		0		0					0								0
2		2	2	2		2			2		2				0
	ω Ω			ω Ω			2		ω Ω		1	2	2		0		2		2 2
		0		0			1 tg	φ	0			4β Ω			ω	Ω			4β Ω
								0				0			ω	Ω			4β Ω
												0
												ω	Ω	2
												2	2

A2	f0		.	(16.7)
	ω02 Ω2	2
			4β2Ω2

Исследуем зависимость A2(Ω). Значения функции на границах области определения

A	0	f	0	, A	0.
A	0			, A	0.

2			2	2
		ω
			0

Функция (16.7) должна иметь максимум. Условие экстремума
				1														2
				1							2	2						2	2
						2 ω						Ω	2 Ω 8β Ω
dA2 0 f				2							0
dA2 0 f				2														3 2		0	,
dΩ		0								2	2					2	2	3 2
dΩ										2	2					2	2
										0
									ω Ω			2	4β Ω
									ω Ω				4β Ω
2β	Ω Ω ω0 Ω							0			Ω 2β								0	;
2β	Ω Ω ω0 Ω							0			Ω 2β					ω0		Ω	0	;
2			2			2									2		2	2
при Ω = 0 функция A2(Ω) имеет минимум, а при

					Ω						ω	2β
											2			2
							рез				0

(16.8)

— резонансной циклической частоте — максимум. Имеет место резонанс — рез-

кое возрастание амплитуды вынужденных колебаний при приближении циклической частоты вынуждающей силы к резонансной циклической частоте.

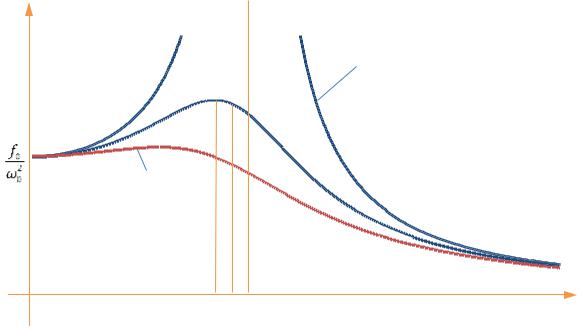
Графики зависимостей A2(Ω) — резонансные кривые — при разных коэффициентах затухания изображены на РИС. 16.5.

Из формулы (16.8) и РИС. 16.5 видно, что Ωрез < ω < ω0. При β → 0 A2 → ∞ — амплитуда вынужденных колебаний в системе без затухания неограниченно возрастает.

Демонстрации: 1) Резонанс на математических маятниках

2)Резонанс на камертонах

3)Двигатель на подставке

136

β = 0

β1

β2 < β1

Ωрез ω ω0

Рис. 16.5

137

Лекция 17

1.15. Механические волны

1.15.1. Уравнение бегущей волны

Волна — любое распространяющееся в пространстве возмущение, т. е. изменение какой-либо физической величины с течением времени.

	 A	 B
0	x1	x2	x
		Рис. 17.1

Пусть величина ξ зависит от времени и это возмущение распространяется со ско-

ростью v — скоростью распространения волны; ξ

волна придёт через время t2 – t1 (РИС. 17.1):

ξ x2 ,t2 ξ x1 ,t1	ξ	x		,t		x	2	x	1
							2		1
			2		1			v
								v

Положим x1 = 0. Тогда в уравнении (17.1) x2 → x, t2 → t,

ξ 0,t f t ,						x
ξ 0,t f t ,		ξ x,t ξ		0,t
						v

					x
	ξ x,t f t				v
					v
— уравнение бегущей волны; t		x	— фаза волны.
— уравнение бегущей волны; t		v	— фаза волны.
		v

= ξ(x, t). Из точки A в точку B

	ξ		x		,t			.	(17.1)
	ξ		x	1	,t		1	.	(17.1)

t		t				x		:
t	1	t				v
	1

			x
f	t		v			;
			v
									(17.2)

1.15.2. Волновой фронт

Волновой фронт (волновая поверхность) — геометрическое место точек, в кото-

рых в один и тот же момент времени колебания происходят в одинаковой фазе.

Часто встречающиеся примеры — плоский и сферический волновой фронт — показаны на РИС. 17.2.

138

Плоская волна

Сферическая волна

волновая поверхность — плоскость	волновая поверхность — сфера
Рис. 17.2
Волны
продольные	поперечные
колебания в направлении	колебания в направлении
распространения волны	перпендикулярном направлению
	распространения волны

ПРИМЕРЫ

Звуковая волна

Электромагнитная волна

Волны на шнуре Волны на поверхности жидкости

Демонстрации: 1) Волны на поверхности жидкости

2)Волны на поверхности жидкости

3)Волновая машина со связями

1.15.3.Гармоническая волна

Гармоническая (монохроматическая, синусоидальная) волна — процесс рас-

пространения гармонических колебаний в пространстве. Уравнение гармонических колебаний

f t Acos ωt φ0 .

Уравнение бегущей волны

ωx

ξ x,t f t

Acos

ωt

φ0

Acos ω t

φ0

139

ξ x,t Acos	ω	t	x	φ
ξ x,t Acos	ω	t		φ
				0
			v

— уравнение плоской бегущей гармонической волны.

Характеристики гармонической волны

Скорость v Начальная фаза φ0

Циклическая частота ω

Период	T	2π
	T	ω


Частота ν			ω	1
Частота ν			2π	T
			2π	T

(17.3)

Амплитуда A — максимальное значение колеблющейся величины.

Длина волны — расстояние, которое волна проходит за время одного полного колебания:

λvT 2πv v

ων

Волновое число

k	2π	ω	2πν	, [k] = м–1.
	λ	v	v

Запишем уравнение (17.9) через волновое число:

ξ x,t Acos ωt

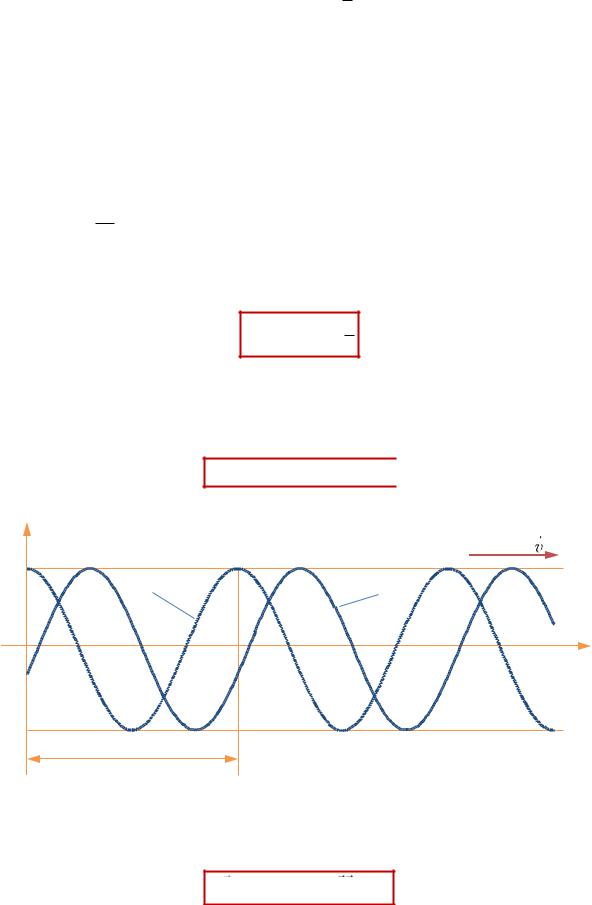
«Мгновенная фотография»

kx φ	.
0	.

гармонической волны

ξ
A	ξ(x, t)	ξ(x, t + t)
	ξ(x, t)	ξ(x, t + t)

0	x
–A
	λ
	Рис. 17.3
Демонстрация:	Волновая машина

В общем случае (при произвольной форме волнового фронта) уравнение бегущей гармонической волны

ξ r,t Acos ωt kr φ0 ,

<<< < Предыдущая 2 3 4 5 6 7 8 9 10 11 12 1314 / 4014 15 16 17 18 19 20 21 22 23 24 25 26 > Следующая >>>

Соседние файлы в папке 2 семестр

#
16.07.20237.88 Mб14Лекции по физике. Лубенченко.pdf
#
16.07.2023684.57 Кб67Сборник задач. Электричество и магнетизм.pdf
#
16.07.2023749.58 Кб8Экзаменационные задачи на 2 семестр.pdf