теория 1к 2с / Приближение функции - практика

Добавил:

ddaren_223 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Российский химико-технологический университет им. Д.И. Менделеева

Предмет:

Программирование на Python

Файл:

yi при i j

j 0,1,2, , n

.pdf

Скачиваний:

Добавлен:

20.06.2023

Размер:

380.78 Кб

Скачать

☆

1 / 21 2 > Следующая >>>

x0, x1, x2, …, xn

Приближение функции.

Для заданных значениях независимой переменной xi и соответствующих им

значениях зависимой переменной yi (i=0,1,2,…,n) определить аналитическую

зависимость. y=f(x)

Основные этапы при приближение функции.

•Выбор вида зависимости

•Выбор критерия

•Выбор узловых точек

•Оценка точности

Интерполяция.

Определение аналитической зависимости функции, между x и y в виде некоторой функции f(x), которая в узловых точках принимает заданные значения.

f(xi)=yi, где i=0,1,2,…,n .

Интерполяция используется для замены реальной сложной функции более простой на небольшом интервале области определения функции, а также для вычислений промежуточных значений функции заданной таблично.

Метод с использование многочлена Лагранжа.

Пусть в n+1 узловой точке определены значения y0, y1, y2, …, yn. Требуется построить многочлен L(x) степени не выше n, который принимает в узловых

точках заданные значения, т.е. L(x0)=y0, L(x1)=y1, L(x2)=y2, …, L(xn)=yn.

Рассмотрим многочлен вида

(x) с

(x x

)(x x

)...(x x

i 1

)(x x

i 1

)...(x x

n 1

)(x x

)

(1)

где i = 0,1,2,3,…….,n, который только в точке xi принимает значение yi , а в остальных

равен нулю.

из этого условия можно определить ci:

i (xi ) ci (xi x0 )(xi x1)...(xi xi 1)(xi xi 1)...(xi xn 1)(xi xn ) yi

)(x

)...(x

)(x

)...(x

)(x

)

i 1

n 1

и тогда многочлен (1) примет вид:

(x) y

(x x

)(x x

)...(x x

i 1

)(x x

i 1

)...(x x

n 1

)(x x

)

(2)

)(x

)...(x

)(x

)...(x

)(x

)

i 1

Многочлен, который в n+1 узловой точке будет принимать заданные значения, можно представить как сумму многочленов вида (2).

	n
	L(x) i (x)
	i 0
n	(x x0 )(x x1 )...(x xi 1 )(x xi 1 )...(x x n 1 )(x x n )
L(x) yi
		2

i 0	(xi x0 )(xi x1 )...(xi xi 1 )(xi xi 1 )...(xi x n 1 )(xi x n )

	Пример. По заданным точкам

	i	0	1	2

	xi	-1.000	0.000	1.000
	yi	1.0000	0.0000	1.0000
Определить интерполяционный многочлен L(x).

	(x) y		(x x			1	)(x x			2	)	1	(x 0)(x 1)	1	x	2	1	x
0		0				1				2						2
					x				x				( 1 0)( 1 1)
			(x				)(x					)		2			2
			(x	0		1	)(x	0			2	)		2			2
				0		1		0			2

	(x) y	(x x0 )(x x 2 )	0	(x 1)(x 1)	0

1	1 (x1 x0 )(x1 x 2 )			(0 1)(0 1)

	(x) y		(x x			0	)(x x			1	)		1	(x 1)(x 0)	1	x	2	1	x
						0				1							2
2		2	(x		x		)(x		x					(1 1)(1 0)
2		2											)		2			2
				2		0		2				1	)		2			2
				2		0		2				1

L(x)=x2

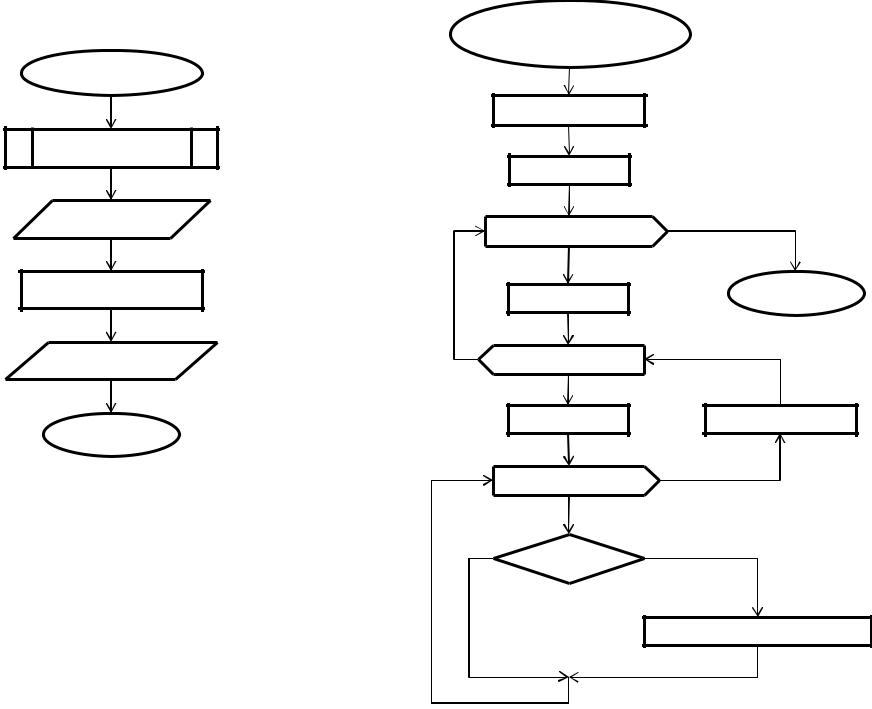
Begin

lagrange(x,y,xz)

x,y,xz

yz=lagrange(x,y,xz)

End

function yr=lagrange(x,y,xz)

nz=length(xz)

n=length(x)

i=1 шаг 1 до nz

yr(i)=0

k=1 шаг 1 до n

pr=1

1 до n

End

yr(i)=yr(i)+pr*y(k)

pr=pr*(xz(i)-x(j))/(x(k)-x(j))

Аппроксимация.

Метод наименьших квадратов

Пусть данные некоторого эксперимента представлены в виде таблицы значений независимой переменной x и зависимой переменной y:

i xi yi

0 x 0 y0

1 x1 y1

2 x 2 y2

n x n yn

Требуется отыскать аналитическую зависимость f(x,a0,a1,…,am), являющуюся функцией одной независимой переменной x и параметров a0,a1,a2,…,am, которая наилучшим образом описывала бы эти экспериментальные данные в смысле минимума квадратичного критерия рассогласования R(a0,a1,…,am):

R yi f (xi , a 0 , a1, , a m ) 2

i 0

Функцию f(x,a0,a1,…,am) определим как полином степени m вида:

f (x, a )

a x a

j 0

Надо найти такие значения параметров, при которых квадратичный критерий

рассогласования имел бы минимальное значение

n	2	m	2

			)	min
R yi (a 0 a1xi a 2 xi		a m xi
i 0

Вывод формулы для определения параметров в матричном виде рассмотрим на примере полинома второй степени (m=2).

_				x2
f (x, a) a	0	a x a	2	x2
	0	1	2

Тогда критерий R будет являться функцией трёх переменных a0,a1,a2 :

n	2	2
		)
R R(a 0,a1, a 2 ) yi (a 0 a1xi a 2 xi
i 0

Необходимые условия минимума критерия R имеют вид:

2 yi (a

) ( 1) 0

0 a1xi a 2 xi

i 0

) ( xi ) 0

2 yi (a 0 a1xi a 2 xi

i 0

) 0

2 yi (a 0 a1xi a 2 xi

) ( xi

i 0

или

a 0

i 0

a 0

a 2

yi xi

i 0

a 0

2 yi xi

i 0

Полученную линейную относительно искомых параметров a0,a1,a2, систему уравнений

запишем в матричном виде:

i 0

N a b

где

i 0

Для удобства формирования матрицы коэффициентов

и столбца свободных членов


введем матрицу	Ф	элементы которой определяются
введем матрицу		элементы которой определяются

через значения независимой переменной xi, i=0,1,2,…,n

		1	1	1	1
	T	1	1	1
N Ф Ф					1
N Ф Ф		x0	x1	xn
		x2	x2	x2
		x2	x2	x2
		0	1	n
					1

x	0	x	2
	0		0
x		x	2	_
x		x
	1	1		b
				b


x		x	2

	n		n
	n		n

		x0			2
	1			x0
		x1			2
	1			x1
Ф

		x		x	2
	1		n		n

T _		1		1
T _
Ф	y x		0	x
			0	1
		x	2	x2
			0	1

тогда

1		y0
1		y
		y
			1
x	2n
x	2n
x	n
	n
		yn
		8

При аппроксимации полиномами высших порядков матрица

будет иметь вид:

	1	x		2	x	m
			0	x		0
				0
	1	x1		2		m	элемент

Ф				x1	x1




	1	x n		2		m
				x n	x n

В общем случае

количество строк в матрицы	Ф	равно

количеству точек, а количество столбцов			Ф

равно количеству параметров, где строка состоит из значений частных производных от функции f(x,a0,a1,…,am) по соответствующему параметру.

			x	j	,
	ij			i

		f (x
				0,

			a		0



f (x
				1,
			a
					0

		f (xn,

			a
					0

Пример. Определить параметры зависимости вида

i 0,1,2,..., n,				j

a )	f (x	0,	a )
		0,
	a
	a
		1

a )	f (x	1,	a )
		1,
	a
	a
		1


a )	f (x	n,	a )
		n,
	a
	a
		1

f (x, a) a0 a1x

0,1,2,..., m

f (x	0,	a )
	0,
a
	m

f (x		a )
	1,
a
	m


f (x	n,	a )
	n,
a
	m

          

используя метод наименьших квадратов, по следующим экспериментальным данным:

	1	1

Ф 1		0
	1	1
		2
	1	2


						1
		1	1	1	1
		1	1	1	1	1
N
			0	1		1
	1		0	1	2	1

						1

4a	0	2a1	9
		6a1
2a0		6a1	8

1

0	4	2
0	4	2

1
1	2	6
2
2


	1.9
a

	0.7

		1	1	1
b
			0	1
	1		0	1

f (x) 1.9 0.7 x

	2
1	1	9

2
2	2	8


	4

R 2.3

1 / 21 2 > Следующая >>>

Соседние файлы в папке теория 1к 2с

#
20.06.2023639.48 Кб908 Встроенные функции.pdf
#
20.06.2023110.75 Кб9Классификация задач и методов оптимизации. Встроенные методы SciPy. - лекция.docx
#
20.06.2023358.63 Кб7Матричные операции и СЛАУ - практика.pdf
#
20.06.2023748.27 Кб7Одномерная оптимизация - практика.pdf
#
20.06.2023911.57 Кб8Построение графиков в Python с использованием модуля matplotlib. - практика.pdf
#
20.06.2023380.78 Кб7Приближение функции - практика.pdf
#
20.06.2023766.12 Кб11Приближение функций. Методы интерполяции зависимостей с одной независимой переменной. Интерполяционный многочлен Лагранжа. Аппроксимация методом наименьших квадратов.pdf
#
20.06.2023736.88 Кб7Решение нелинейного уравнения - практика (1).pdf