2. Площадь в криволинейных координатах

Пусть система (1) взаимно однозначно отображает замкнутую область G плоскости UOV на замкнутую область D плоскости XOY. Предположим, что функции  и  непрерывны вместе со своими частными производными на G. Предположим, что G и D квадрируемы.

Задача. Выразить площадь области D с помощью криволинейных координат u, v.

Р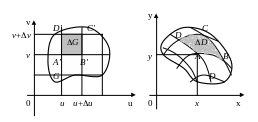 азобьем область G на частичные области прямыми, параллельными осям Ou и Ov. Тогда область D разобьётся в силу преобразования (1) на криволинейные четырёхугольники. Рассмотрим внутренний элементарный прямоугольник в плоскости UOV с вершинами в точках

(u,v>0).

Ему соответствует элементарный криволинейный четырёхугольник в плоскости XOY с вершинами

.

Найдём его площадь .

Если u и v достаточно малы, то дуги тоже малы, следовательно, их приблизительно можно считать прямолинейными. Кроме того, приращения функций x(u;v), y(u;v) приблизительно заменим их дифференциалами. Тогда

.

Аналогично,

,

, .

А также

,

,

.

Тогда приблизительно координаты вершин четырёхугольника ABCD:

,

, .

(Здесь для краткости: x(u;v)=x, y(u;v)=y, все производные вычислены в т. (u;v)).

Из координат видим, что проекции отрезков AB и CD на обе оси координат соответственно равны, следовательно, AB║CD. То же можно сказать и об отрезках AD и BC: AD║BC. Значит, приближенно ABCD – параллелограмм.

.

Из геометрии известно, что , где :

, где .

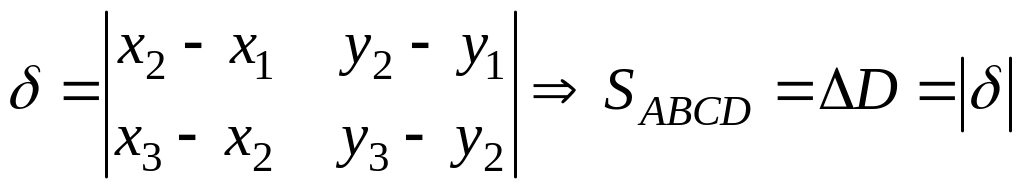По этой формуле получим:

.

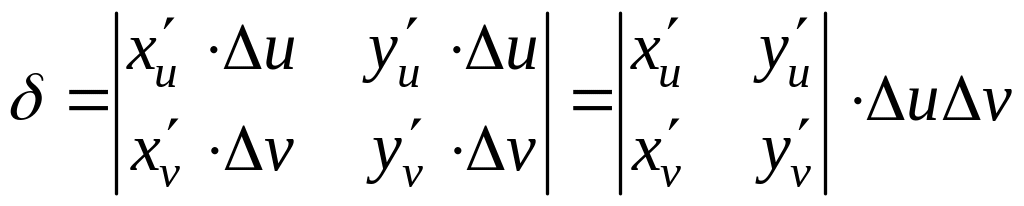Обозначим .

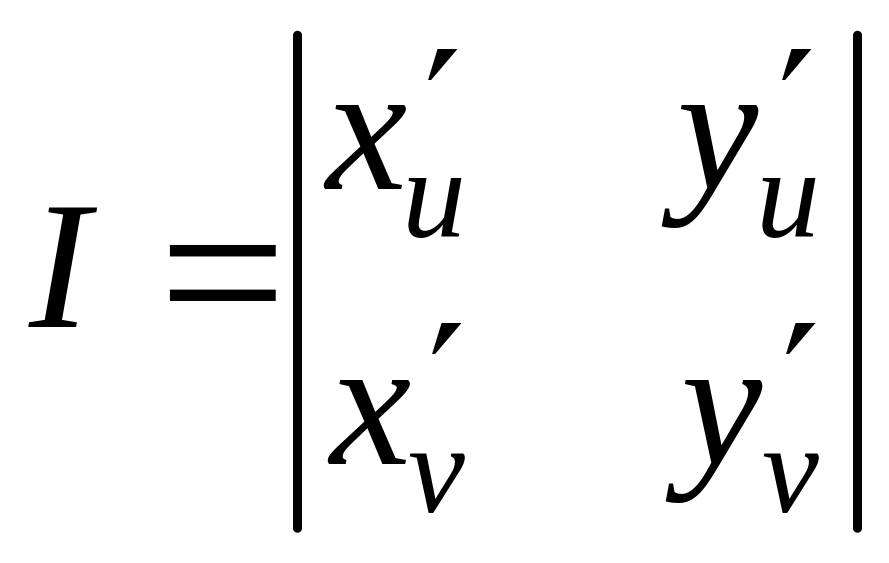Этот определитель называется якобианом. Следовательно,

. (3)

Выражение в правой части называется элементом площади в криволинейных координатах.

Учитывая, что , из формулы (3) получим .

Это приближенное равенство тем точнее, чем меньше . Следовательно, если u0 и v0, то .

Величина |I(u;v)| показывает, во сколько раз увеличивается или уменьшается элемент площади в окрестности точки (u;v) плоскости UOV при отображении её в окрестность соответствующей точки (x;y) плоскости XOY. Другими словами, абсолютная величина якобиана – это коэффициент растяжения области G в данной точке (u;v) при её отображении на область D.

Просуммировав теперь площади всех элементарных четырехугольников, из (3) получим

. (4)

Это равенство тем точнее, чем мельче разбиение области G (а, следовательно, и области D). Переходя к пределу при и , получим точное равенство. Сумма в правой части равенства (4) является интегральной суммой для двойного интеграла , из которой выброшены слагаемые, отвечающие участкам, не являющимся прямоугольниками. Но сумма площадей этих участков становится сколь угодно малой, если разбиение делать более мелким. Следовательно, переход к пределу в (4) даёт точную формулу

. (5)

Вычислим якобиан при переходе к полярным координатам:

.

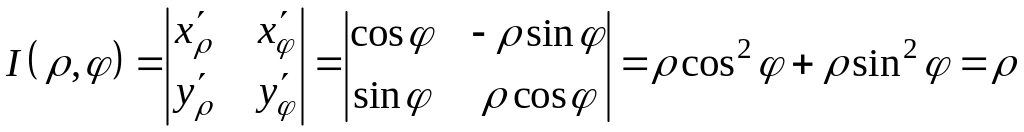Следовательно, площадь D при переходе к полярным координатам равна:

.

3. Замена переменной в двойном интеграле

Теорема. Пусть дан двойной интеграл , где функция f(x;y) непрерывна в замкнутой квадрируемой области D. Пусть система

(1)

задаёт взаимно однозначное отображение замкнутой квадрируемой области G плоскости UOV на замкнутую квадрируемую область D плоскости XOY. Предположим, что функции  и  непрерывны вместе со своими частными производными на G. Пусть так же |I(u;v)|0 на D. Тогда справедлива формула замены переменных

. (6)

Доказательство.

Так как функции f, ,  и частные производные функций  и  непрерывны, то существуют оба интеграла в формуле (6). Необходимо доказать это равенство.

По определению двойного интеграла

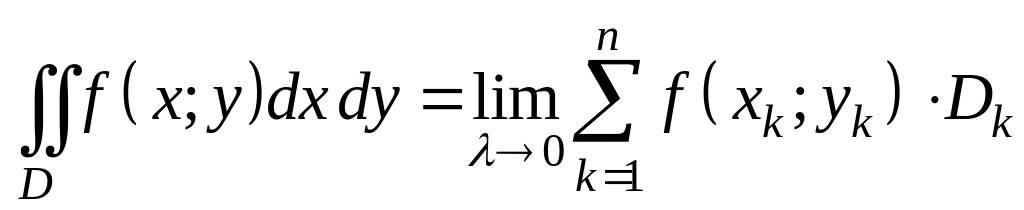, (7)

( - диаметр разбиения), причём этот предел не зависит от способа разбиения области D на частичные области D_k и от выбора точек (x_k;y_k) D_k. Обозначим .

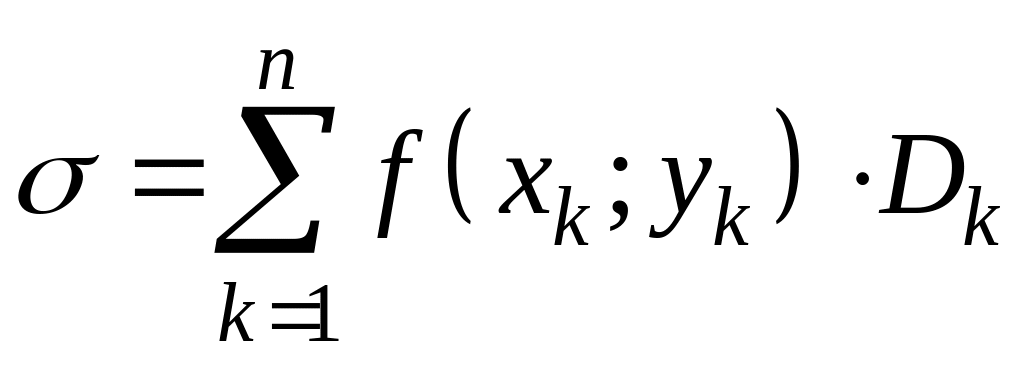Разобьём область G на частичные области . Так как (1) взаимно однозначно отображает G на D, то область D разобьётся на частичные области . По формуле (5) площадь области D_k равна:

.

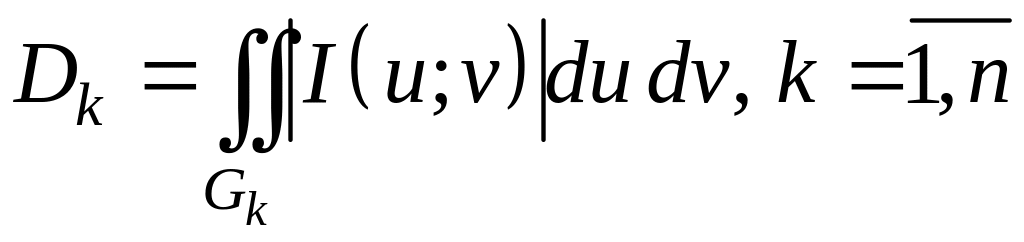По теореме о среднем значении двойного интеграла на каждой частичной области найдется точка (u_k;v_k), такая, что

.

Обозначим образ т. (u_k;v_k) при взаимно однозначном отображении (1) через (x_k;y_k), то есть

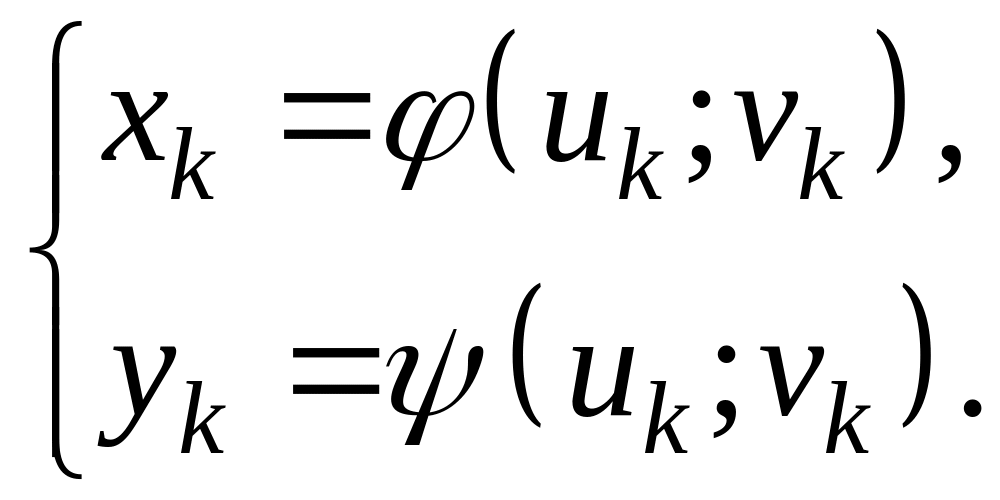
Тогда сумма  в правой части равенства (7) равна

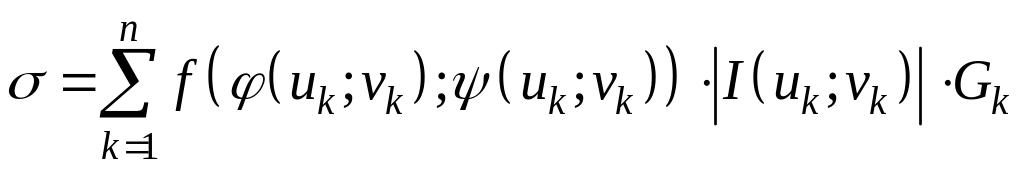. (8)

Эта сумма является интегральной суммой для функции .

Если диаметры всех частичных областей G_k стремятся к нулю, то в силу непрерывности функций  и  диаметры частичных областей D_k тоже стремятся к нулю. Обозначим , . Если , то и . Переходя в (8) к пределу при , получим (6).

Замечание. Формула (6) справедлива и в том случае, если взаимно однозначное отображение (1) нарушается в отдельных точках или на отдельных кривых площади нуль.