2448

С ростом A пикфактор резко увеличивается. Большое значение пикфактора нежелательно и не всегда допустимо, поскольку связано с неоправданной тратой времени и ресурсов на раскрытие маловероятных, а, иногда, и малозначащих состояний объекта.

Если использовать неоптимальный в данном случае дихотомический алгоритм поиска с деревом, показанным на рис. 5.3, то среднее число измерений (алгоритмическая скрытность) R log2 A 3, что в полтора раза больше потен-

циального значения.

На рис. 6.5 показаны КСН для оптимального последовательного (кривая 1) и дихотомического (кривая 2) алгоритмов при тех же параметрах, что и рис. 6.4. Отклонение от оптимальности поиска приводит к повышению скрытности и снижению информативности первых измерений.

Рис. 6.5

6.3.2. Равномерное распределении вероятностей состояний объекта

Пусть X – симметричное множество возможных равновероятных состояний объекта со значением A 2n , где n – це-

лое число, Pi 1/ A , i 1, A . В этом случае оптимальным яв-

ляется дихотомический алгоритм поиска, дерево которого при A 8 показано на рис. 5.3. Исходная энтропия множества со-

нет нужды рассматривать для усреднения все варианты ветвей дерева поиска, так как они одинаковы.

Нетрудно показать, что средняя энтропия состояний H (N) имеет вид

Если при равномерном распределении вероятностей использовать неоптимальный последовательный алгоритм поиска, то повысится скрытность (алгоритмическая) которая равна

алгоритма поиска и определить ее в виде

RS . (6.20)

В рассматриваемом случае S log2 A и с учетом (6.19) получим

Зависимость (A) показана на рис. 6.7а. Как видно, из-

быточность алгоритма последовательного поиска возрастает при увеличении A .

Рис. 6.7

На рис. 6.7б представлены КСН для дихотомического (кривая 1) и последовательного (кривая 2) поиска. В данном случае переход к последовательному перебору состояний резко ухудшает информационную эффективность поиска.

61

Глава 7. СКРЫТНОСТЬ ПЕРВОГО И ВТОРОГО РОДА

7.1.Скрытность первого рода

Впредыдущих главах рассматривались ситуации, в кото-

рых при единственном реасобытии и отсутствии ошибок

измерения всегда можно построить алгоритм поиска и обеспечить достоверное выявление всех состояний объекта с нулевой неопределенностью (энтропией) результата.

Однако на практике это не всегда возможно. В измерительном канале присутствуют помехи, которые приводят к ошибочным измерениям. Они могут исправляться в ходе дополнительных (проверочных) измерений, однако всегда останется некоторая неуверенность в результате поиска. Помимо реасобытия могут наблюдаться и другие, близкие по свойствам (например, маскирующие сигналы), и тогда разведка не приведет к правильному результату при сколь угодно продолжительном поиске.

Таким образом, в общем случае оптимальный алгоритм поиска должен проектироваться так, чтобы обеспечивать минимум двоичных измерений для выявления реасобытия с заданной достоверностью, если она достижима. Вероятность правильного обнаружения реасобытия будем называть дове-

рительной и обозначать Pдов

Полученную скрытность объекта (алгоритмическую или потенциальную) будем называть скрытностью первого рода и обозначать R1 или S1 соответственно. Она характеризует

фактические затраты, необходимые для решения задачи поиска.

7.2. Скрытность второго рода

Если вероятность правильного выявления реасобытия xr

меньше единицы, то с ненулевыми остаточными вероятно62

стями Pостi истинным может быть другое значение xi .

На рис. 7.1 показан пример такого распределения вероятностей (в логарифмическом масштабе) при условии обнаружения реасобытия x4

с вероятностью Pдов 0.9 ,

A 8 .

Оставшаяся после завершения поиска неопределенРис.7.1 ность характеризуется оста-

точной энтропией

i1

Вобщем случае она зависит от характеристик объекта, алгоритма поиска и значения реасобытия.

При заданной величине Pдов для найденного xr максимум H ост имеет место при равных вероятностях всех остальных состояний объекта,

Тогда наибольшее возможное значение остаточной энтропии равно

Hост max Pдов log2 Pдов (1 Pдов )log2 (1 Pдов ) (1 Pдов )log2 (A 1) . (7.3)

63

Зависимости Hост max от доверительной вероятности Pдов и арсенала множества состояний A показаны на рис. 7.2.

Рис.7.2

Как видно, наибольшее значение остаточной энтропии уменьшается с повышением доверительной вероятности обнаружения состояния объекта и уменьшением A .

Величина H ост характеризует неопределенность о реасо-

бытии после окончания поиска, когда измерения прекращаются и принято окончательное решение. Тогда ее можно рас-

сматривать как остаточную энтропийную скрытность объ-

екта – скрытность второго рода S2 , которая оценивает ми-

нимально необходимое число гипотетических двоичных измерений, которые необходимо было бы произвести для точного выявления реасобытия, если бы поиск продолжался безошибочно. Тогда с учетом (7.1) получим

рода в единую оценку скрытности объекта удобно ввести понятие комплексной скрытности S , определив ее равенством

64

где j 1 - мнимая единица. Все эти виды скрытности из-

меряются в двоичных измерениях.

В отличии от скрытности первого рода остаточная скрытность характеризует условные (фиктивные) затраты на поиск, который никогда не реализуется, и для него отсутствует необходимость в разработке оптимальных алгоритмов. Поэтому для ее оценки вполне подходит остаточная энтропия (7.4).

7.3. Симптомы

На практике весьма часто приходится иметь дело не с недоступными непосредственно для осмотра или исследования состояниями, а с определенными признаками состояний. Условимся называть их симптомами в широком понимании этого слова в разных областях приложения.

В квартире погас свет. Это может быть следствием ряда факторов, определяющих обстановку: неисправности электролампы, предохранителя, выключателя и т.д. Темнота в квартире является зримым синдромом неисправности сети; конкретная причина подлежит выявлению.

Один и тот же симптом может быть следствием ряда факторов xi, определяющих состояние объекта или обстановки и наоборот. Повышенная температура, головная боль – симптомы заболевания, которое не всегда может быть выявлено путем даже самых тщательных исследований.

Радиолокационный сигнал в виде отметки на экране индикатора может быть вызван действительным появлением цели в зоне наблюдения, но может быть вызван выбросом напряжения шума на выходе приемника. Общепринятыми стали перекочевавшие из радиолокации в связь и другие области выражения «ложная тревога» и «пропуск сигнала».

Сигналы с разными параметрами, несущими частотами, например xi , являются симптомами действия станций в диа-

65

пазоне, но не всегда отражают истинную обстановку из-за помех или умышленных ложных излучений.

Будем, как и прежде, обозначать множество состояний

объекта через X {xi }, i 1, A , множество симптомов – через Y {y j }, j 1, B . Мощности этих множеств могут быть раз-

ными, как по числу элементов, так и по вызывающих их причинам и физическим обстоятельствам.

7.4. Вероятности симптомов и их скрытность

Симптомы далеко не всегда лежат «на поверхности», часто для их выявления требуются более или менее сложные и трудоемкие измерения (анализы). В связи с этим возникает вопрос об оптимизации поисковых процедур в пространстве симптомов.

На рис. 7.3а в виде двух столбцов символов в кружках представлены множества X и Y с их элементами xi и yi . Их объединяют так называемые переходные (условные) вероят-

При известном законе распределения вероятностей состояний объекта P(xi ) и матрице [Pj / i ] вероятности симпто-

мов (их закон распределения) можно найти по формуле полной вероятности

Потенциальная энтропийная скрытность множества симптомов вычисляется по формуле

Рис. 7.3

Симптомы рассматриваются при этом как состояния y j

некоторого объекта Y , отделенного от Х. Скрытность (7.6) указывает , как и в случае с Х , на минимально необходимое, в среднем, число двоичных измерений (диз) для раскрытия симптомов (скрытность первого рода).

При отсутствии помех и неоднозначности состояния xi и симптомы yi на диаграмме рис. 7.4а связаны между собой

прямыми линиями без перекрещиваний, что может быть выражено равенством

Матрица переходных вероятностей принимает при этом

67

диагональный вид (рис. 7.4б) с единицами по диагоналям и нулями в других клетках.

Рис. 7.4

7.5. Апостериорные вероятности состояний исследуемого объекта после измерений

При измерениях (анализах) мы устанавливаем симптомы yi состояний исследуемого объекта Х с заданным априорным

законом распределения вероятностей P(xi ) . Выявленные симптомы по мере их раскрытия меняют наши представления о состояниях xi (их вероятностях). Мы стремимся к выяснению интересующих нас деталей обстановки до пределов воз-

или, с учетом (7.5),

68

P(xi )P( y j / xi )

i 1

Апостериорная вероятность xi определяется, как видно, удельным вкладом P(xi )P( y j / xi ) в сумму вкладов в P( y j ) всех xi с учетом переходных вероятностей в знаменателе вы-

ражения (7.9). Рассматриваемое как функция целочисленной переменной i , это выражение представляет закон распределения апостериорных вероятностей состояний исследуемого объекта Х. Значение P(xi / y j ) в (7.9) зависит от степени соот-

ветствия симптомов истинным состояниям объектов. Если при j i P( yi / xi ) 1 , то P( y j / xi ) 0 при j i и каждому симптому соответствует единственное состояние. В этом случае апостериорные и априорные распределения вероятностей совпадают. На практике симптомы отбираются исходя из степени их взаимосвязи с выявляемыми состояниями, а в противном случае их использование нецелесообразно.

В табл. 7.1 приведен пример априорного закона распределения вероятностей состояний объекта Pi P(xi ) при А=4.

Таблица 7.1

На рис. 7.5 представлена матрица переходных вероятностей [Pj / i ] симптомов и состояний, а на рис. 7.6 – диаграммы

апостериорных вероятностей P(xi / y j ) , полученных согласно (7.9).

69

Рис. 7.5

Рис.7.6

Как видно из рис 7.6.а, признак x1 сильно статистически связан с симптомом y1 (вероятность их совпадения 0,917).

Аналогичные выводы следуют и из диаграмм на рис. 7.6б – рис. 7.6г, но с меньшими вероятностями. Если реасобытие определяется по максимальной апостериорной вероятности симптома, то ее значение является доверительной вероятностью Pдов принятого решения.

По окончании поиска симптомов остается неопределен70

ность относительно соответствующего состояния, которая характеризуется условной энтропией

Она представляет собой остаточную скрытность состояния после завершения поиска симптомов,

реходных вероятностей типа рис. 7.4б апостериорное распределение имеет вид

после выявления симптома неопределенность состояния (остаточная скрытность) равна нулю.

71

птома. Это означает, что симптомы не содержат информации о состояниях и обнаруженный в процессе поиска симптом не позволяет судить об имеющемся состоянии.

Апостериорные распределения типа рис. 7.6 сами по себе могут служить наглядным и численно обоснованным выражением результатов исследования объекта и обстановки.

7.6. Информационные характеристики и остаточная неопределенность

Исходная неопределенность H (X ) состояний объекта определяется выражением (4.1),

После выявления симптома в процессе поиска условная энтропия состояний, усредненная по симптомам, с учетом

(7.10) равна

Это средняя остаточная неопределенность (скрытность второго рода S2 ) состояний, обусловленная неоднозначностью со-

ответствия симптомов и состояний объекта. Если между симптомами и состояниями имеется однозначное соответствие (7.12), то остаточная неопределенность равна нулю. Если же статистическая взаимосвязь между ними отсутствует, то есть

72

тогда остаточная энтропия равна исходной,

и после завершения поиска неопределенность состояний не снижается.

В результате поиска наблюдатель получает общее количество информации, равное

Оно зависит от вероятностных свойств состояний и матрицы переходных вероятностей (взаимосвязи симптомов и состояний) и изменяется от нуля до H (X ) .

В теории информации доказано, что безусловная энтропия не меньше условной, то есть количество информации неотрицательно. Там же показано, что

Безусловные и условные вероятности и энтропии симптомов зависят как от свойств состояний, так и от матрицы переходных вероятностей.

Величина H(Y) является энтропийной скрытностью симптомов (скрытностью первого рода S1 ) и характеризует за-

траты на их безошибочное выявление.

Следует иметь в виду, что энтропийные скрытности первого и второго рода в данном случае относятся к различным множествам симптомов и состояний соответственно.

73

7.7. Отгадывание

В том случае, когда получение информации о состоянии объекта невозможно из-за дефицита времени, сильных помех или обрыва измерительного канала, остается еще шанс его отгадывания.

Возможны две стратегии в этой задаче – неприцельное и прицельное отгадывание.

Неприцельное отгадывание предполагает равновероятный выбор реасобытия xr (путем «слепого» выбора из урны биле-

ятностей независимых событий равна произведению P(xr )Q(xr ) . Поскольку совпадение может иметь место при любом xr , для вычисления вероятности отгадывания необхо-

димо усреднить это произведение по всем реасобытиям. Тогда вероятность отгадывания равна

Отсюда следует, что независимо от закона распределения вероятностей состояний объекта P(xi ) вероятность непри-

цельного отгадывания равна 1/ A . Она убывает по гиперболическому закону с увеличением ассортимента возможных состояний А.

Если распределение вероятностей реасобытий существенно неравномерно, то целесообразней использовать прицельное отгадывание.

В этом случае в качестве реасобытия выбирается наиболее вероятное значение xi , в соответствии с чем вероятность

74

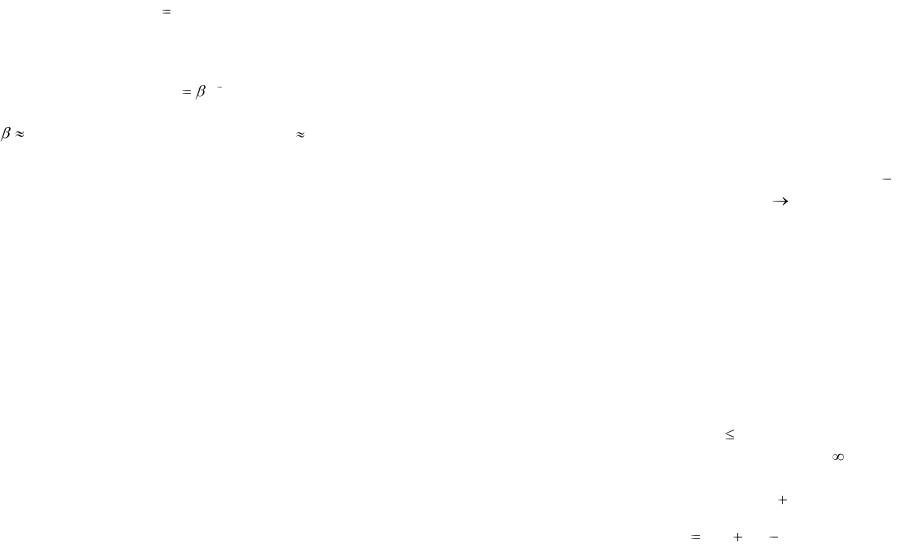
прицельного отгадывания может быть представлена в выражением

чительно больше по сравнению с (7.19) при больших А.

При прицельном отгадывании и заданном распределении вероятностей P(xi ) всегда будет выбираться то состояние, для которого выполняется условие (7.20).

При отгадывании скрытность первого рода S1 равна нулю, так как поиск не проводится, а остаточная скрытность S2 максимальна и равна исходной энтропии состояний H (X ) .

75

Глава 8. СКРЫТНОСТЬ ОБЪЕКТОВ С НЕПРЕРЫВНЫМ МНОЖЕСТВОМ СОСТОЯНИЙ

8.1. Особенности непрерывных множеств состояний

Непрерывным (континуальным) является такое множество состояний объекта X , в котором на любом конечном интервале находится бесконечное множество значений состояния. Точки непрерывного множества расположены «вплотную» друг к другу, а вероятность p выбора конкретного зна-

чения состояния бесконечно мала (стремится к нулю).

При оценке скрытности состояний объекта с конечном числом состояний ее величина пропорциональна log(p) и

стремится к бесконечности при p 0 . Таким образом, рас-

смотренный математический аппарат оказывается неприемлемым для анализа скрытности состояний с непрерывным множеством значений.

8.2. Плотность вероятностей

В теории вероятностей [2] при описании статистических свойств непрерывных случайных величин x используется

плотность вероятностей w(x) .

Определим функцию распределения вероятностей F(x) значения непрерывной вещественной случайной величины как вероятность того, что x . Эта величина конечна и изменяется от 0 при до 1 при . Тогда вероятность p(x) попадания значения случайной величины в беско-

и ее значения бесконечно малы.

Для перехода к конечным функциям используется плот76

ность вероятностей w(x) случайной величины, определяемая выражением

И числитель, и знаменатель в выражении (8.2) бесконечно малы, а их отношение может быть любым положительным числом.

По определению функции распределения вероятностей получим условие нормировки

При заданной плотности вероятностей w(x) функция распределения вероятностей F(x) определяется выражением

Вероятность попадания значения случайной величины в интервал от x1 до x2 равна

x1

Из (8.2) следует

77

тогда полагая dx сколь угодно малой, но конечной величиной, при анализе скрытности непрерывных состояний можно использовать результаты анализа, полученные для дискрет-

скую) непрерывную случайную величину, плотность вероятностей которой имеет вид

различных СКО показаны на рис.8.1, а при 1 и различных a - на рис. 8.2.

Рис. 8.1

Как видно, среднее значение a определяет центр функции распределения вероятностей, а СКО – ширину кривой (область разброса значений случайной величины). При отклонении x от среднего плотность вероятностей резко уменьша-

78