Дискретная математика & математическая логика

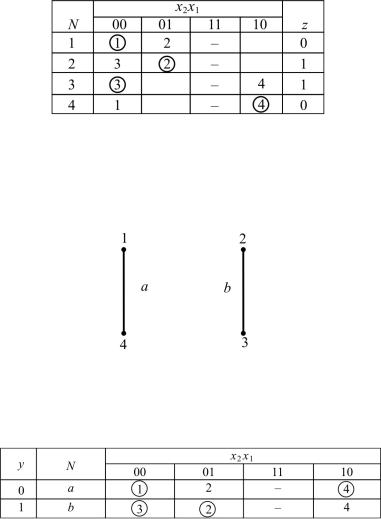
Таким образом, последовательность детерминированная. Построим первичную таблицу переходов-выходов:

Считается, что реле х2 исправно и ситуация 11 не возникает. Переход из 4-го такта в 1-й обусловлен естественным снижением температуры до следующего нагрева. Строим граф объединения строк (рис. 6.4):

Рис. 6.4. Граф объединения строк

Таким образом, получаем всего две строки. Строим минимизированную таблицу переходов:

201

Определяем все переходы:

поэтому карта Карно тривиальна (на одну переменную):

Получим таблицу переходов-выходов, не строя реализуемую таблицу переходов. Выходные сигналы кодируем для автомата Мура, т.е. выходные сигналы формируются после перехода в очередное состояние, а до этого, в неустойчивом такте действует выходной сигнал предыдущего устойчивого такта.

В тактах 1, 4 и строках z = 0, в тактах 2, 3 и строках z = 1. Получим символическую форму записи функций, описываю-

щих автомат:

y(t + 1) = D(t) = P(t) = 1, 4, 5 [0, 2, 6],

z = 4, 5, 6 [0, 1, 2].

Абстрактный синтез завершен. Проводим минимизацию по таблице переходов-выходов (начинаем структурный синтез):

y(t + 1) = D(t) = P(t) = (1 3 5 7) (4 5) → (–1) (10–) = x1 y x2 ,

z = y(t).

202

Построим релейно-контактную схему (рис. 6.5):

Рис. 6.5. Схема автомата

6.3. СИНТЕЗ СИНХРОННОГО АВТОМАТА

6.3.1. Синтез счётчика

Для синтеза счётчика на базе триггеров и логических элементов удобно использовать таблицу переходов-выходов в виде карты Карно. Текущее состояние счетчика сопоставляется с кодом клетки, а последующее указывается внутри клетки. Автомат синхронный, устойчивых состояний нет.

Пусть необходимо синтезировать счетчик с коэффициентом счета 5 на базе JK-триггеров. Построим граф переходов, у которого будет5 вершин– рис. 6.6:

Рис. 6.6. Граф переходов счётчика с коэффициентом счёта 5

203

Ввиду того, что коэффициент счёта 5, необходимо три элемента памяти (intlog52 = 3). Получим таблицу переходов-выходов, вкоторой указывается, как автомат-счетчик переходит из текущего

Код клетки – это соединение (конкатенация) двоичного кода строки и столбца, представленное в виде двоичного числа (выделены курсивом). Внутри клетки выделены жирным шрифтом последующие состояния счётчика, их всего 5.

Используя таблицу возбуждения JK-триггера,

получим таблицу возбуждения заданного счётчика:

204

Из таблицы (она же карта Карно) получим минимизированные функции управления триггерами:

J3 = y2 y1 , J2 = y1 , J1 = y3 , K3 = 1, K2 = y1 , K1 = 1.

По этим функциям и строится схема логического преобразователя счётчика. Такой счётчик – самый быстрый, с параллельным переносом, состояние всех триггеров изменяется одновременно по синхроимпульсу.

6.3.2. Синтез автомата-распознавателя с повторяющимися символами

Пример. Синтезируем синхронный автомат, распознающий последовательность 0–0–2–2. На правильную последовательность срабатывает индикатор z1, что значит «замок открыт». Для всех неверных наборов срабатывает z 2, что значит «замок закрыт» или «замок заблокирован».

Проведём блочный синтез (рис. 6.7):

Рис. 6.7. Разбиение автомата на блоки

При нажатии кнопки кодопреобразователь x/y формирует код а и активирует одновибратор, синхронизирующий дискретный автомат ДА. Переход осуществляется при нажатии очередной кнопки – срабатывает одновибратор и формирует один синхроимпульс.

205

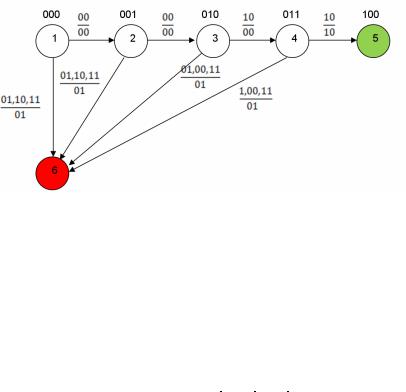
Приступим к этапу абстрактного синтеза дискретного автомата ДА. Построим граф переходов для нашего синхронного автома-

та (рис. 6.8):

Рис. 6.8. Граф переходов автомата 0022

На рис. 6.8. стрелками обозначены переходы из одного состояния в другое. Дробные значения над стрелками: в числителе условия переходов в последующее состояние, в знаменателе – получаемое выходное значение. Цветом обозначены конечные состояния автомата, зелёный – для разрешённой последовательности 0022, красный – для запрещённых.

Используя рис. 6.8, строим таблицу переходов автомата Мура

0022:

Можно построить автомат Мура, в котором в состоянии 5

(100)формируется сигнал z1 – открытие «замка», а в состоянии 6

(101)– z 2 – тревога, подбор кода.

206

Построим таблицу переходов-выходов автомата Мили 0022:

ния функций в символической форме абстрактный синтез заканчивается.

Регулярные языки и конечные автоматы

Пусть имеется алфавит А = {а1, а2, …, аs}. Одноэлементные языки а1, а2, …, аs, а также язык, содержащий только пустое слово Λ(λ , ε), будем называть элементарными языками [12].

Регулярным языком называется такой язык, который можно получить из элементарных языков с помощью конечного числа операций сложения, умножения и итерации.

Чтобы доказать регулярность какого-либо языка, надо записать его в виде так называемого регулярного выражения, т.е. формулы, в которой конечное число раз используются элементарные языки и знаки операций сложения, умножения и итерации.

207

Автомат с начальным состоянием v1 и заключительным состоянием v3 задан диаграммой Мура (рис. 6.9):

Рис. 6.9. Диаграмма (граф) Мура некоторого автомата

Соответствующий автомату язык L задаётся регулярным выражением

b (a + b)* + a·b*·а (a + b)*,

где * – звёздочка Клини, означающая итерацию.

Основная теорема теории автоматов. Язык L распознает-

ся конечным детерминированным автоматом тогда и только тогда, когда L – регулярный язык.

Конечные автоматы широко используются на практике, например в синтаксических, лексических анализаторах и тестировании программного обеспечения.

В соответствии с одной из классификаций языков можно различать:

–автоматы-распознаватели. Множество всех слов, распознаваемых автоматом – язык;

–автоматы-формирователи. Они формируют регулярные выражения языка;

–автоматы-преобразователи. Они могут преобразовывать выражение одного языка в выражение другого языка («переводить»).

208

7. ЭЛЕМЕНТЫ ТЕОРИИ ИГР

Теория игр – это математическая теория конфликтов. Конфликт – ситуация, в которой сталкиваются интересы сторон, происходит борьба интересов (например, война, военный конфликт). Другие примеры конфликтов – игры – шашки, шахматы, спортивные игры. Они ведутся по определённым правилам: дан перечень возможных ходов и прописано, к какому результату приводит некоторая совокупность ходов.

Далеко не каждый конфликт протекает по правилам (вспомним выражения «бои без правил», «русские воюют не по правилам»). Для математического анализа конфликта необходимо представить конфликт в игровой форме, т.е. указать стратегии (возможные действия) и уточнить, к какому результату приведёт игра, если каждый игрок выберет определённую стратегию.

Таким образом, игра – это конфликт с чётко сформулированными условиями.

Часто результат игры даже при определённых стратегиях предсказать невозможно, так как всё зависит от случая. Тогда говорят о среднем результате, т.е. о результате, приходящемся в среднем на одну партию, если будет сыграно достаточно большое число партий, т.е. даже если кому-то случайно везёт, в среднем выигрывает тот, кто ведёт себя разумно.

Часто результат выражается числом, даже если это просто выигрыш (1) или проигрыш (0). Мы будем полагать, что выигрыш (проигрыш) каждого игрока выражается числом.

Основная задача теории игр формулируется так: как должен вести себя (какую стратегию применять) разумный игрок в конфликте с разумным противником (противниками), чтобы обеспечить себе в среднем наибольший возможный выигрыш?

209

Парные игры

Если в конфликте участвуют две стороны, то игра называется парной, если несколько – множественной. Мы ограничимся рассмотрением парных игр.

Игры с нулевой суммой

Игра называется игрой с нулевой суммой, если одна сторона выигрывает то, что проигрывает другая. Иногда такую игру называют антагонистической. Случается, что один игрок выигрывает одну сумму, а другой в этой же ситуации проигрывает другую.

Конечные игры

Конечные игры – это игры, в которых каждый игрок располагает конечным числом стратегий. В этом, помимо всего прочего, выражается своего рода дискретность игры.

Платёжная матрица

Платёжная матрица, или матрица (таблица) игры с нулевой суммой:

Здесь К – « красный» игрок, С – « синий». У красного три стратегии, у синего четыре. kij – выигрыш (проигрыш) «красного», т.е. проигрыш (выигрыш) «синего».

Если игра представлена в виде такой таблицы (матрицы), то говорят, что игра приведена к нормальной форме. Записать шахматы в нормальной форме очень трудно.

210