
Дискретная математика & математическая логика
..pdf
Таблица 3 . 2
Решение транспортной задачи по критерию времени tmax = 4
Номер |
Маршрут |
Частичный поток |
Время прохождения |
маршрута |
(xi, yj) |
ϕ k |
потока |
k |
|
|
tij |
1 |
(x2, y2) |
10 |
1 |
|
((x2, х5)) |
|
|
2 |
(x1, y4) |
10 |
2 |
|
((x1, х7)) |
|
|
3 |
(x3, y4) |
5 |
3 |
|
((x3, х7)) |
|
|
4 |
(x2, y1) |
5 |
4 |
|
((x2, х4)) |
|
|
5 |
(x3, y3) |
20 |
4 |
|
((x3, х6)) |
|
|
|
|
50 |
tmax = 4 |
3.5. ЗАДАЧА О ЗНАКОМСТВАХ И ТЕОРИЯ РАМСЕЯ
Средитрёхчеловеквсегданайдутсядвоеодногопола– рис. 3.20:
Рис. 3.20. Задача о знакомствах для n = 3
Обозначим красным цветом инверсное отношение – рис. 3.21:
91
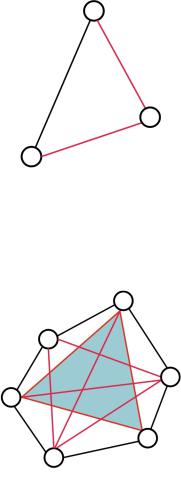
Рис. 3.21. Отношение «бытьразногопола»
Всегда найдётся либо чёрная (отношение «быть одного пола» – «однополность»), либокрасная(«разнополность») линия!
Рассмотрим отношение знакомства в группе из шести человек. Например– рис. 3.22.
Рис. 3.22. Вариант отношения знакомства в группе из шести человек
Можно убедиться, что при любых вариантах обязательно найдётся либо красный (три незнакомых), либо чёрный (три знакомых) треугольник! А вот если мы возьмем пять человек – это свойство не выполняется. Например, может сложиться следующая ситуация – рис. 3.23.
92

Рис. 3.23. Вариант отношения знакомства в группе из пяти человек
Здесь нет ни красного, ни чёрного треугольника, поэтому шестёрка является экстремальной (в данном случае наименьшей) характеристикой, при которой выполняется требуемое свойство – три человека либо знакомы, либо незнакомы.
Задача о знакомствах положила начало новому направлению в комбинаторике – теории Рамсея. Одна из базовых задач – определение наименьшего значения числа людей R(n), из которых можно выбрать либо n попарно незнакомых, либо n попарно знакомых. Установлено, что R(4) = 18, но дальнейшие точные значения пока неизвестны. Талантливый математик Фрэнк Рамсей доказал, что полная неупорядоченность невозможна.
Каждое достаточно большое множество чисел, точек или объектов обязательно содержит высокоупорядоченную структуру.
Головоломка о вечеринке представляет собой задачу, типичную для приложений теории Рамсея (1905–1930) – рис. 3.24. Она формулируется так: какое количество людей достаточно для того, чтобы образовать группу, в которой всегда окажется либо четверо людей, знакомых друг с другом, либо четверо, друг с другом незнакомых? На этом рисунке гости представлены точками. Каждое красное ребро на этом графе соединяет гостей, знакомых друг
93

с другом, а каждое синее – незнакомых. В группе из 17 точек, изображённых на рисунке, невозможно найти четыре точки для которых сеть соединяющих их рёбер была бы целиком красной или целиком синей.
Рис. 3.24. Головоломка о вечеринке
Таким образом, требуется более 17 человек, чтобы среди них обязательно оказалось либо четверо знакомых, либо четверо незнакомых друг с другом. На самом деле, во всякой группе из 18 человек всегда найдутся либо четверо знакомых, либо четверо незнакомых друг с другом.
Фрэнк |
Рамсей, впервые доказавший |
это утверждение |
в 1928 году, |
вырос в Кембридже – рис. 3.25. |
Его отец, Артур |
С. Рамсей, был профессором математики и президентом колледжа Магдалины Кембриджского университета. В 1925 году молодой Рамсей, признанный самым лучшим студентом в изучении математики, окончил университет. Хотя больше всего его интересовали философия и математическая логика, он также писал работы по экономике, теории вероятности, принятию решений, когнитивной психологии и семантике.
94

Рис. 3.25. Фрэнк Рамсей
Вскоре после окончания университета он вошёл в группу экономистов, которую возглавлял Джон Мэйнард Кейнс. Рамсей написал лишь две статьи по математической экономике, но обе до сих пор широко цитируются. Что касается философии, то его вдохновляли идеи Джорджа И. Мура, Людвига Витгенштейна и Бертрана Рассела. Мур писал: «Он необычайно ясно мыслил: никто не мог легче его избежать тех логических погрешностей, от которых несвободны даже лучшие философы». Затем произошла трагедия: в 1930 году Рамсей заболел и в 26 лет умер от осложнений после операции.
За два года до смерти Рамсей вывел теорию, ныне называемую его именем. Он пришёл к основной идее, пытаясь доказать тезис, выдвинутый Бертраном Расселом и Альфредом Нортом Уайтхедом в их основополагающем труде ’Principia Mathematica’ («Основы математики»). Они предположили, что все математические истины могут быть выведены из ограниченного набора аксиом. Развивая эту идею, немецкий математик Давид Гильберт предположил, что должна существовать процедура, позволяющая решить, следует ли то или иное утверждение из данного набора аксиом, или нет. Рамсей показал, что в некотором частном случае такая проце-
95

дура принятия решения существует. (Спустя несколько лет Курт Гёдель и его последователи, англичанин Алан Тьюринг и другие, исчерпывающим образом доказали, что в общем случае такой процедуры не существует.) Рамсей доказал свою теорему в качестве первого шага, пытаясь продемонстрировать справедливость тезиса Рассела в специальном случае.
3.6. ПОКРЫТИЯ, НЕЗАВИСИМОСТЬ, СВЯЗНОСТЬ
Вершина покрывает инцидентные ей ребра. Ребро покрывает инцидентные ему вершины. Множество вершин, покрывающих все ребра, – это вершинное покрытие. Наименьшее число вершин во всех вершинных покрытиях называется числом вершинного покрытия – а0. Множество ребер, покрывающих все вершины, – это реберное покрытие. Наименьшее число рёбер во всех рёберных покрытиях – а1 [4].
Дан граф (рис. 3.26):
Рис. 3.26. Некоторый граф
Построим матрицу инцидентности для данного графа:
|
t1 |
t2 |
t3 |
а |
1 |
1 |
0 |
b |
0 |
1 |
1 |
с |
1 |
0 |
1 |
96
Получим покрытие вершинами рёбер:
(a c)(a b)(b =c) (a bc)(b = c) ab ac bbc= bcc ab ac bc.
Получим покрытие рёбрами вершин:
(t t |
2 |
)(t t |
3 |
)(t |
t=) (t |
2 |
t t |
)(t =t |
3 |
) |
||||
1 |
2 |
|
|
1 |
3 |
1 3 |
1 |
|
|
|
||||
= t t |
|
t t t |
|
t |
2 |
t |
t t =t |
t t |
t t |
t t |
|
. |
||
1 2 |
|
1 1 3 |
|
|
3 |
1 3 3 |
1 2 |
|
1 3 |
1 3 |
|
|||
Наименьшее покрытие
Если вершине (ребру) поставлена в соответствие некоторая цена, возникает задача о наименьшем покрытии. Например, задача о переводчиках, из которых каждый владеет несколькими языками; задача о перевозке – доставке товаров потребителям, в которой производится выбор маршрутов с минимальными транспортными расходами.
Независимость
Множество вершин независимо, если никакие две из них не смежны. Наибольшее число вершин в независимом множестве вершин – вершинное число независимости β0. Множество рёбер независимо, если никакие два из них не смежны.
Наибольшее число ребер в независимом множестве рёбер – это рёберное число независимости β1. Числа независимости и покрытия связаны друг с другом и с количеством вершин p. Для любого нетривиального связного графа
а0 + β0 = а1 + β1 = p.
Пусть имеется множество процессов, использующих неразделяемые ресурсы. Соединим рёбрами процессы (вершины), которым требуется один и тот же ресурс. Тогда β0 – количество возможных параллельных процессов.
97

Связность и сильная связность
В связном графе любые две вершины соединены простой цепью. Граф связен тогда, когда его нельзя представить в виде объединения двух графов (объединения компонент связности).
Мост – это ребро, удаление которого увеличивает число компонент связности. Блок – это граф, не имеющий точек сочленения (это концы мостов).
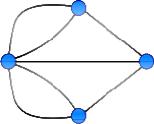
На рис. 3.27 показаны диаграммы сильно, односторонне и слабо связанных орграфов.
а |
б |
в |
Рис. 3.27. Диаграммы орграфов: а – сильная связность; б – односторонняя связность; в – слабая связность
Вершинной (рёберной) мерой связности называется наименьшее число вершин (рёбер), удаление которых приводит к получению несвязного графа.
В ориентированном графе отношение связности несимметрично, поэтому вводятся понятия:
–сильной связности (две вершины сильно связаны, если существует путь, т.е. ориентированная цепь из одной в другую и наоборот);
–две вершины односторонне связаны, если существует только один путь;
–две вершины слабо связаны, если они связаны только при отмене ориентации дуг.
98
3.7. ЭЙЛЕРОВЫ И ГАМИЛЬТОНОВЫ ГРАФЫ
Эйлеров граф. Задача о кёнигсбергских мостах
Эйлеров путь (эйлерова цепь) [3] в графе – это путь, проходящий по всем рёбрам графа и притом только по одному разу.
Теорема. Эйлеров путь в графе существует тогда и только тогда, когда граф связный и содержит не более чем две вершины нечетной степени, т.е. ни одной вершины, одна вершина, две вершины.
Эйлеров цикл – это эйлеров путь, являющийся циклом. Эйлеров граф – граф, содержащий эйлеров цикл. Конечно, эйлеров цикл ипуть существуют только в связных графах или в графах, которые послеудалениявсех одиночных вершин превратятсяв связные.
В неориентированном графе согласно теореме, доказанной Эйлером, эйлеров цикл существует тогда и только тогда, когда в графе отсутствуютвершинынечетной степени.
Рис. 3.28. Граф кёнигсбергских мостов
Граф кенигсбергских мостов. Этот граф не является эйлеро-
вым, поэтому решения не существует (рис. 3.28). На карте старого Кёнигсберга был мост, появившийся позже других и соединивший остров Ломзе с южной стороной. Своим появлением этот мост обязан самой задаче Эйлера – Канта. А произошло это вот как.
Кайзер Вильгельм славился своей солдатской прямотой. Однажды, находясь на светском рауте, он чуть не стал жертвой шутки, которую с ним решили сыграть учёные умы, присут-
99

ствующие на приёме. Они показали кайзеру карту Кёнигсберга и попросили попробовать решить эту знаменитую задачу, которая по определению была нерешаемой. Ко всеобщему удивлению кайзер попросил перо и лист бумаги, сказав, что решит задачу за полторы минуты. Ошеломлённый немецкий истеблишмент не мог поверить своим ушам, но бумагу и чернила быстро нашли. Кайзер положил листок на стол, взял перо и написал: «Приказываю построить восьмой мост на острове Ломзе». Так в Кёнигсберге и появился новый мост, который так и назвали – Мост кайзера.
На рис. 3.29 показан пример некоторого эйлерова графа:
Рис. 3.29. Некоторый эйлеров граф
Каждая вершина графа рис. 3.29 имеет чётную степень, поэтому этот граф – эйлеров. Обход ребер в алфавитном порядке дает эйлеров цикл.
Эйлеров цикл в ориентированном графе. Связный ориен-
тированный граф содержит эйлеров цикл тогда и только тогда, когда для каждой вершины графа её полустепень захода равна её полустепени исхода, т.е. в вершину входит столько же рёбер, сколько изнеёвыходит.
100
