Краткий курс общей физики

Введя обозначения

где – коэффициент затухания; 0 – собственная циклическая частота колебаний системы (частота, с которой происходили бы свободные колебания системы при отсутствии сопротивления среды, т.е. при r = 0), перепишем уравнение движения следующим образом:

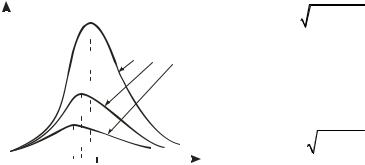
На рис. 1.31 представлен график функции (1.134). Пунктирными линиями показаны пределы, в которых изменяется смещение колеблющейся точки х.

При слабом затухании движение системы можно рассматривать как гармоническое колебание с частотой з и амплитудой, изменяющейся по закону:

Верхняя из пунктирных кривых на рис. 1.31 дает график функции А(t), причем величина А0 представляет собой амплитуду в начальный момент времени.

61

Характеристики затухания

Коэффициент затухания характеризует скорость затухания колебаний:

Логарифмический декремент затухания – натуральный лога-

рифм от декремента затухания:

За время система успевает совершить Ne = /T колебаний. Логарифмический декремент затухания – величина, обратная числу колебаний, совершаемых за время релаксации :

1 . (1.142)

Ne

Добротность Q системы – величина, пропорциональная числу колебаний, совершаемых за время релаксации :

62

1.3.5. Вынужденные колебания

Вынужденными называются такие колебания, которые возникают в колебательной системе под действием внешней периодически изменяющейся силы (вынуждающей силы). Пусть вынуждающая сила изменяется со временем по гармоническому закону:

где – частота вынуждающей силы; F0 – ее амплитуда.

При составлении уравнения движения (второго закона Ньютона) кроме вынуждающей силы необходимо учесть также и те силы, которые действуют в системе при свободных колебаниях, т.е. квазиупругую и силу сопротивления среды: max kx rvx F0 cos t .

С учетом обозначений (1.132) приходим к дифференциальному уравнению вынужденных колебаний:

Это неоднородное (правая часть отлична от нуля) дифференциальное уравнение второго порядка с постоянными коэффициентами. Как известно из теории дифференциальных уравнений, общее решение неоднородного уравнения равно сумме общего решения (1.134) однородного уравнения (1.133), соответствующего данному неоднородному, и частного решения данного неоднородного урав-

Амплитуду A и отставание по фазе можно найти, непосредственноподставляячастноерешение(1.146) вуравнение(1.145), откуда:

Общее решение уравнения (1.145), описывающее поведение системы при вынужденных колебаниях, имеет вид

x A0e t cos( зt ) Acos( t ).

63

Первое слагаемое в этом уравнении играет заметную роль только в начальной стадии процесса при установлении колебаний. С течением времени из-за экспоненциального множителя e t роль этого слагаемого уменьшается, и по прошествии достаточного времени им можно пренебречь, сохраняя лишь второе слагаемое.

Таким образом, функция (1.146) описывает установившиеся вынужденные колебания. Они представляют собой гармонические колебания с частотой, равной частоте вынуждающей силы. Амплитуда (1.147) вынужденных колебаний пропорциональна амплитуде вынуждающей силы. Для данной колебательной системы амплитуда зависит от частоты вынуждающей силы. Вынужденные колебания отстают по фазе от вынуждающей силы, причем величина отставания также зависит от частоты вынуждающей силы (см. фор-

мулу (1.148)).

Зависимость амплитуды вынужденных колебаний от частоты вынуждающей силы приводит к тому, что при некоторой определенной для данной системы частоте амплитуда колебаний достигает максимального значения. Явление резкого возрастания амплитуды вынужденных колебаний при приближении частоты вынуждающей силы к некоторому значению, называется резонансом, а соответствующая частота – резонансной частотой рез.

Выражение для резонансной частоты получаем, исследовав функцию (1.147) на максимум:

частоты вынуждающей силы и от коэффициента затухания. Видно, что максимум резонансной кривой смещен влево по оси от 0; это смещение будет тем больше, чем больше коэффициент затухания .

64

Вредные и полезные проявления резонансных явлений наблюдаются в природе и технике. Резонанс полезен в тех случаях, когда необходимо обнаружить слабые колебания или усилить их. На этом явлении основана вся аппаратура, воспринимающая и усиливающая звуковые и электрические колебания.

Нередко явление механического резонанса служит причиной катастроф. Например, собственная частота вибраций корпуса корабля или крыльев самолета должна сильно отличаться от частоты колебаний, которые могут быть возбуждены вращением гребного винта или пропеллера. В противном случае могут возникнуть разрушения. При вращении плохо отцентрированного мотора вследствие резонанса может произойти его поломка и повреждение фундамента здания, на котором расположен мотор.

1.3.6. Волновое движение

Распространение волн в упругой среде

Колебания, возбужденные в какой-либо точке среды (твердой, жидкой или газообразной), передаются от одной точки среды к другой и распространяются в ней с конечной скоростью, зависящей от свойств среды. Чем дальше расположена частица среды от источника колебаний, тем позднее она начинает колебаться. Иначе говоря, фазы колебаний частиц среды и источника тем больше отличаются друг от друга, чем больше расстояние между частицей и источником. При изучении распространения колебаний не учитывается дискретное (молекулярное) строение среды, она рассматривается как сплошная, т.е. непрерывно распределенная в пространстве и обладающая упругими свойствами.

Процесс распространения колебаний в сплошной среде называется волновым движением или волной. При распространении волны частицы среды не движутся вместе с волной, а колеблются около своих положений равновесия. Вместе с волной от частицы к частице среды передаются лишь состояние колебательного движения и его энергия. Поэтому основным свойством всех волн, независимо от их природы, является перенос энергии без переноса вещества.

Волны могут иметь различную форму:

а) одиночная волна, или импульс, – короткое возмущение, не имеющее регулярного характера (рис. 1.33, а);

65

на волны равна тому расстоянию, на которое распространяется волна (определенная фаза колебания) за период:

где частота колебаний, = 1/T.

Если рассмотреть волновой процесс подробнее, то ясно, что колеблются не только частицы, расположенные вдоль оси х, но и совокупность частиц, расположенных в некотором объеме, т.е. волна, распространяясь от источника колебаний, охватывает все новые и новые области пространства. Геометрическое место точек, до которых колебания доходят к моменту времени t, называется

волновым фронтом.

Геометрическое место точек, колеблющихся в одинаковой фазе, называется волновой поверхностью. Волновых поверхностей можно провести бесчисленное множество, а волновой фронт в каждый момент времени один. Волновой фронт также является волновой поверхностью. В принципе волновые поверхности могут быть любой формы, а в простейшем случае они представляют собой совокупность плоскостей, параллельных друг другу, или совокупность концентрических сфер. Соответственно волна называется

плоской или сферической.

Уравнения плоской и сферической волн. Волновое уравнение

Уравнением волны называется выражение, которое дает смещение колеблющейся точки как функцию ее координат и времени:

= (x, y, z, t).

Найдем вид функции в случае плоской волны, распространяющейся вдоль оси x (см. рис. 1.34). В данном случае волновые поверхности перпендикулярны оси x, а так как все точки волновой поверхности колеблются одинаково, то смещение будет зависеть только от x и t, т.е. = (x, t).

Рассмотрим некоторую частицу среды В (см. рис. 1.34), находящуюся от источника колебаний на расстоянии х. Если колебания точек, лежащих в плоскости х = 0, описываются функцией(0, t) = A cos( t + ), то частица среды В колеблется по тому же

67

закону, но ее колебания будут отставать по времени от колебаний источника на , так как для прохождения волной расстояния х требуется время = x/v, где v – скорость распространения волны.

Тогда уравнение колебания частиц, лежащих в плоскости х, имеет вид

откуда следует, что (x, t) является не только периодической функцией времени, но и периодической функцией координаты х.

Зафиксируем значение фазы волны:

t x const.v

Взяв дифференциал этого выражения и сократив на , получим dt dvx 0, откуда ddxt v. Следовательно, скорость v распростра-

нения волны в уравнении (1.153) есть не что иное, как скорость перемещения фазы волны, поэтому ее называют фазовой скоростью.

Для характеристики волн используется также волновое число

где ( t – kx + ) – фаза распространяющейся волны; – начальная фаза, зависящая от выбора начала отсчета х и t.

Уравнение (1.155) называют уравнением плоской волны. Если плоскаяволнараспространяетсявпротивоположном направлении, то

Если плоская волна (1.155) или (1.156) распространяется в среде, не поглощающей энергию, то амплитуда волны А = const.

Повторяя ход рассуждений для плоской волны, можно показать, что уравнение сферической волны, волновые поверхности ко-

68

где A0 – амплитуда на расстоянии r = 1; r – расстояние от центра волны до рассматриваемой точки среды.

В случае сферической волны даже в среде, не поглощающей энергию, амплитуда колебаний не остается постоянной, а убывает с расстоянием по закону 1/r, поскольку энергия волновой поверхности распространяется по все большей площади (S = 4 r2).

Если фазовая скорость волн зависит от их частоты, то это явление называется дисперсией волн, а среда, в которой наблюдается дисперсия волн, диспергирующей средой.

Уравнение любой волны есть решение некоторого дифференциального уравнения, называемого волновым. Для плоской волны, распространяющейся вдоль оси х, волновое уравнение имеет вид

Энергия упругих волн. Вектор Умова

Бегущими называются волны, которые переносят в пространстве энергию. Если поглощением энергии при распространении волны пренебречь, то можно считать, что вся энергия колебаний W частиц среды целиком определяется энергетическим излучением источника (см. соотношение (1.103)):

W mA2 2 , 2

где m – масса среды, вовлеченной в колебательный процесс.

Эта энергия передается частицам среды от источника и распределена в пространстве неравномерно. Средняя объемная плотность энергии, переносимой волной,

где ρ ‒ плотность среды, в которой распространяется волна, Vm .

Итак, среда, в которой возникает волна, обладает дополнительным запасом энергии. Эта энергия доставляется от источника колебаний в различные точки среды самой волной, следовательно, волна переносит с собой энергию. Количество энергии, переносимое волной через некоторую поверхность в единицу времени, называется потоком энергии Ф через эту поверхность:

69

Поток энергии – скалярная величина, размерность которой равна размерности энергии, деленной на размерность времени, т.е. совпадает с размерностью мощности: [Ф] = Вт.

Поток энергии в разных точках среды может обладать различной интенсивностью. Для характеристики переноса энергии в разных точках пространства вводится векторная величина, называемая

плотностью потока энергии j . Этот вектор для упругих волн на-

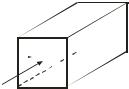
зывается вектором Умова. Направление вектора Умова совпадает с направлением переноса энергии, а его модуль равен энергии, переносимой волной за единицу времени через единичную площадку, расположенную перпендикулярно направлению распространения волны (рис. 1.35):

Интенсивность волны J – среднее значение энергии, переносимой волной за единицу времени через единичную площадку, расположеннуюперпендикулярнонаправлениюраспространения волны:

Интерференция волн

При одновременном распространении нескольких волн колебания частиц среды оказываются геометрической суммой колебаний, которые совершали бы частицы при распространении каждой из волн в отдельности, т.е. волны просто накладываются одна на другую, не возмущая друг друга. Это утверждение называется принци-

пом суперпозиции (наложения) волн.

Вслучае когда колебания, обусловленные отдельными волнами

вкаждой из точек среды, обладают постоянной разностью фаз, волны называют когерентными. Очевидно, что когерентными могут быть лишь волны, имеющие одинаковую частоту. В более широком смысле под когерентностью понимают согласованное протекание двух и более колебательных или волновых процессов.

70