Сопротивление материалов курс лекций

Из сказанного можно сделать следующий вывод: если какаялибо ось проходит через центр тяжести сечения, то статический момент площади сечения относительной этой оси равен нулю; и наоборот, если статический момент относительно какой-либо оси обращается в нуль, то эта ось является центральной.

Понятие о моментах инерции сечения

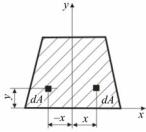
Осевым моментом инерции сечения относительно данной оси называется взятая по всей площади сечения сумма произведений элементарных площадок на квадраты их расстояний до этой оси

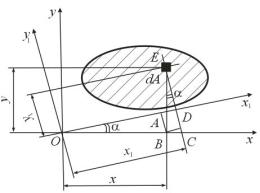
(см. рис. 4.1):

Полярным моментом инерции сечения относительно некоторой точки (полюса 0) называется взятая по всей его площади сумма произведений элементарных площадок на квадраты их расстояний до полюса:

Осевые и полярный моменты инерции являются величинами существенно положительными. Пользуясь рис. 4.1, установим связь между полярным и осевым моментами инерции сечения:

Iρ =∫ρ2dA =∫(x2 + y2 )dA =∫x2dA+∫y2dA.

т.е. полярный момент инерции равен сумме осевых моментов инерции относительно любой пары взаимно перпендикулярных осей, проходящих через полюс.

51

Центробежным моментом инерции сечения относительно не-

которых двух взаимно перпендикулярных осей называется взятая по всей его площади сумма произведений элементарных площадок на их расстояния до этих осей:

В зависимости от расположения осей центробежный момент инерции может бытьположительным, отрицательным и равным нулю.

Рассмотрим центробежный момент инерции сечения относительно осей, одна из которых является осью симметрии фигуры (рис. 4.3). Легко заметить, что для каждой положительной величины xydA в пер-

вом квадранте можно найти такую же отрицательную во втором квадранте, т.е. для

Рис. 4.3. всей фигуры

Ixy =∫xydA =0.

A

Итак, если хотя бы одна из осей является осью симметрии фигуры, то центробежный момент инерции сечения относительно этой оси и любой ей перпендикулярной равен нулю. Оси, относительно которых центробежный момент инерции равен нулю, называются главными. Если начало координат этих осей совпадает с центром тяжести сечения, то их называют главными центральными.

Из определения моментов инерции (4.5), (4.8) очевидно, что они характеризуют расположение сечения относительно осей. Размерность моментовинерции – (единица длины)4; например, мм4, см4, м4.

Моменты инерции простых сечений

Прямоугольник (рис. 4.4)

Вычислим моменты инерции относительно главных центральных осей x и y . Для определения момента инерции относительно

52

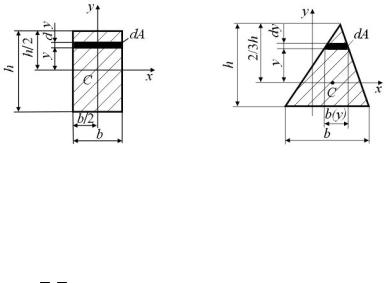
оси выделим элементарную площадку в виде узкого прямоугольника, параллельного оси x :

dA=bdy.

Момент инерции находим по формуле (4.5):

Очевидно, что относительно другой главной центральной оси y момент инерции определяется как

Треугольник (рис. 4.5)

Найдем момент инерции относительно центральной оси x. Выделим элементарную площадку ввиде полоски, параллельной оси x:

dA=b( y)dy,

где b( y)=bh (23 h−y).

В соответствии с формулой (4.5) получим:

53

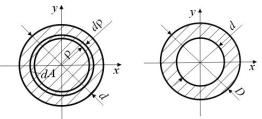
Круг (рис. 4.6)

Вычислим полярный момент инерции круга относительно его центра. Для этого радиусами ρ и (ρ+dρ) выделим произвольно

расположенное бесконечно тонкое кольцо, площадь которого найдем как площадь прямоугольника со сторонами 2πρ и dρ:

dA=2πρdρ.

Рис. 4.6. Рис. 4.7.

Полярный момент инерции круга

Моменты инерции круга относительно центральных осей легко найти на основании зависимости (4.7). В силу симметрии

Ix =I y ,

следовательно,

Кольцо (рис. 4.7)

Моменты инерции кругового кольца определяются точно так же, как круга, но с учетом изменения нижнего предела интегрирования в связи с наличием отверстия:

54

где α – коэффициент ослабления сечения, величина которого зави-

сит от размера отверстия, α= Dd .

На основании соотношения (4.7) может быть получена формула для осевого момента инерции кольца:

Моменты инерции сложных сечений

При вычислении моментов инерции сложных сечений последние разбивают на отдельные простые составляющие фигуры, моменты инерции которых известны. Из основного свойства интеграла следует, что момент инерции сложной фигуры равен сумме моментов инерции составляющих ее частей.

Найдем момент инерции сложного сечения относительно оси x (см. рис. 4.2). Разобьем сечение на простые фигуры. При вычислении будем последовательно суммировать произведения y2dA , охватывая площади A1, A2 , A3 простых фигур. Тогда

Ix =∫y2dA = ∫ y2dA+ ∫ y2dA+ ∫ y2dA.

IxI , IxII , IxIII , т.е.

Ix =IxI +IxII +IxIII .

Таким образом, для сложных сечений моменты инерции связаны следующими соотношениями:

55

с отрицательной площадью.

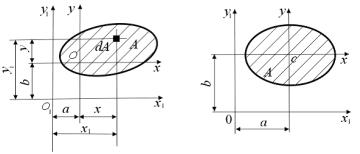
Зависимость между моментами инерции при параллельном переносе осей координат

Пусть известны моменты инерции произвольного сечения относительно взаимно перпендикулярных осей x, y (рис. 4.8, а), кото-

рые определены согласно формулам (4.5) и (4.8):

Рис. 4.8.

Найдем моменты инерции относительно осей x1, y1 , которые параллельны заданным осям x, y:

Ix 1 =∫y12dA; I y1 =∫x12dA; Ix1y1 =∫x1 y1dA.

A A A

Координаты любой точки в новой системе x1, y1 могут быть выражены через координаты в осях x, y:

56

x1 =x+a, y1 = y +b.

где a, b – координаты старого начала координат осей x, y в новой системе x1, y1 . Подставляя значение y1 в выражение для Ix1 , имеем

Ix1 =∫( y +b)2 dA =∫y2dA+2b∫ydA+b2 ∫dA.

Аналогично может быть найдено выражение для момента инерции относительно оси y1 :

Если исходные оси являются центральными (см. рис. 4.8, б), то формулы при параллельном переносе осей упрощаются, так как статические моменты Sx , Sy обращаются в нуль:

Отметим, что в последнюю из этих формул координаты a, b следует подставлять с учетом их знака (в системе координат x1, y1 ).

Следует подчеркнуть, что относительно любой нецентральной оси осевые моменты инерции больше, чем относительно параллельной ей центральной.

Зависимость между моментами инерции при повороте осей координат

Будем считать известными моменты инерции сечения Ix , Iy , Ixy . Определим моменты инерции Ix1 , I y1 , Ix1y1 относительно осей x1, y1

(рис. 4.9), повернутых на угол α (напомним, что в правой системе координат α > 0 при повороте против хода часовой стрелки).

Рис. 4.9.

Установим связь между координатами x1, y1 и x, y:

x1 =ОD =ОА+АD =ОА+ВС или x1 =x cosα+y sin α.

Аналогично найдем y1 : y1 =СЕ−DС, y 1= y cosα−xsin α.

По определению, Ix1 =∫y12dA, после подстановки y1 имеем

A

58

Ix1 =∫( y cosα−xsin α)2 dA =cos2 α∫y2dA−

A A

−2sin αcosα∫xydA+sin2 α∫x2dA.

A A

Учитывая, что

получаем

Ix1 =Ix cos2 α+I y sin2 α−Ixy sin 2α.

Используя известные тригонометрические соотношения

Складывая почленно выражения (4.21) и (4.22), получаем

Ix1 +Iy1 =Ix +I y =Iρ =const ,

т.е. при повороте осей сумма осевых моментов инерции не изменяется. Следовательно, если один момент инерции возрастает, то другой убывает; один достигает максимального значения, другой – минимального.

59

Исследуем функцию (4.21) на экстремум, чтобы установить оси, относительно которых осевые моменты инерции сечения экстремальны:

Таким образом, условием экстремальности осевых моментов инерции является равенство нулю центробежного момента инерции относительно этих осей, т.е. осевые моменты инерции имеют максимальное и минимальное значения относительно главных осей, которым в случае несимметричных сечений дают свои обозначения, например u и v.

Рассмотрим частный случай задачи, в которой известны моменты инерции относительно главных осей Iu , Iv ( Iuv =0 ), а требуется

определить осевые и центробежные моменты инерции сечения относительно осей x, y, повернутых от главных осей u, v на угол α.

Нужные формулы легко получить из соотношений (4.21), (4.22), (4.23):

Ixy = Iu −Iv sin 2α. 2

Определение направления главных осей. Главные моменты инерции

По определению, центробежный момент инерции относительно главных осей u и v равен нулю, т.е. Iuv = 0. Приравнивая к нулю правую часть выражения (4.23) при α=α0 , получим:

60