Сопротивление материалов курс лекций

Пример 15.2. На гранях элемента (рис. 15.7), находящегося в ПНС, заданы напряжения:

σx =160 ΜΠa, σy = 60 ΜΠa, τxy = 40 ΜΠa.

Определить: a) главные напряжения и положения главных площадок; б) напряжения в элементе, повёрнутом к исходному на 45°; в) наибольшие касательные напряжения.

Рис. 15.7.

Аналитическое решение

1. По формуле (15.4) определим положение главных площадок:

Величина главных напряжений может быть найдена по (15.6)

Исходя из полученных результатов, изобразим главный элемент

(рис. 15.8).

201

Рис. 15.8.

2. Напряжение на грани элемента, повёрнутого на 45°, найдём по (15.1)

По найденным значениям изобразим на рис. 15.9 рассмотренные площадки и действующие на них напряжения.

Рис. 15.9.

3. Наибольшие касательные напряжения найдём по (15.8):

202

τmax = σ1 −2 σ3 = 1742−0 =87 МПа.

Графическое решение

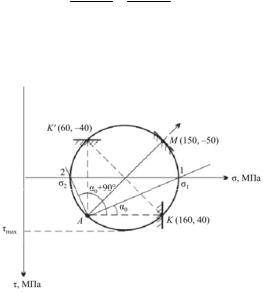
Построим круг Мора по изображающим точкам K (160, 40)

и K′(60, –40) (рис. 15.10).

Рис. 15.10.

Полюс круга A найдем на пересечении нормалей к исходным площадкам.

Круг пересечёт горизонтальную ось в точках 1 и 2. Точка 1 соответствует главному напряжению σ1 = 174 МПа, точка 2 – значению главного напряжения σ2 = 46 МПа. Луч, проведенный из полюса A через точки 1 и 2, покажет значение главных углов. Напряжения на площадке, повёрнутой на 45° к исходной, равны координатам изображающей точки M, находящейся на пересечении окружности с лучом, проведенным из полюса A под углом 45°.

Как видим, графическое решение задачи анализа напряжённого состояния совпадает с аналитическим.

203

Лекция 16

ЭЛЕМЕНТЫ ТЕОРИИ ДЕФОРМИРОВАННОГО СОСТОЯНИЯ В ТОЧКЕ ТЕЛА

Как было сказано ранее, деформированным состоянием в точке тела называют совокупность деформаций по различным осям и в различных плоскостях, проходящих через данную точку, а сами де-

мальными напряжениями на гранях элемента, а угловые деформации зависят только от касательных напряжений. Подобно тому, как для описания напряженного состояния в точке тела был использован тензор напряжений Tσ, для деформированного состояния введем

тензор деформаций:

Между компонентами тензоров Тσ и Тε существует прямая математическая аналогия, поэтому все формулы, полученные при анализе напряженного состояния, остаются справедливыми при замене нормальных напряжений на линейные деформации: σx →εx ,

σy →εy , σz →εz , а касательных напряжений – на половину соответствующих величин угловых деформаций:

204

Главным напряжениям σ1, σ2 , σ3 соответствуют главные ли-

нейные деформации ε1, ε2 , ε3 . При этом главные направления обоих

тензоров для упругого изотропного тела совпадают, главные деформации экстремальны, а угловые деформации на главных площадках равны нулю.

Обобщённый закон Гука

При рассмотрении растяжения и сжатия мы выяснили, что линейная деформация в продольном направлении связана с напряжением в поперечном сечении стержня законом Гука:

ε= Εσ .

При этом в поперечном направлении возникает деформация, которая определяется через продольную деформацию с помощью коэффициента Пуассона:

ε׳=−µε=−µ Εσ .

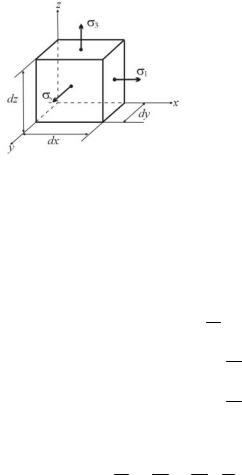
Для того чтобы обобщить ранее полученный результат на случай объёмного напряженного состояния, рассмотрим деформацию элементарного параллелепипеда размерами dx, dy, dz. Ориентацию

элемента выберем такой, чтобы по его граням действовали главные напряжения σ1, σ2 , σ3 , т.е. координатные оси совпадали с главными

направлениями (рис. 16.1).

Вследствие деформации длины рёбер изменятся и станут равными dx+∆dx, dy +∆dy, dz +∆dz. Относительные удлинения ребер

параллелепипеда представляют собой главные деформации:

205

На основании принципа суперпозиции можно записать:

ε1 =ε11 +ε12 +ε13 ,

где ε11 – линейная деформация в

направлении первого главного напряжения, вызванного действием только σ1;

ε12 – линейная деформация в Рис. 16.1. том же направлении, вызванная дей-

ствием главного напряжения σ2; ε13 – линейная деформация в том же направлении от действия

напряжения σ3.

Направление σ1 для самого напряжения σ1 является продольным, а для напряжений σ2 и σ3 – поперечным, поэтому

ε11 =σΕ1 ,

σ

ε12 =−µ Ε2 ,

σ

ε13 =−µ Ε3 .

Сложив эти величины, получим:

ε1 =σΕ1 −µ σΕ2 −µ σΕ3 = Ε1 σ1 −µ(σ2 +σ3 ).

206

Проделав аналогичные выводы для двух других главных направлений, получим:

Выражения (16.2) представляют собой обобщенный закон Гука для главных деформаций. Поскольку деформации принимаются малыми, влиянием сдвигов на линейные деформации можно пренебречь и считать формулы (16.2) справедливыми не только для главных деформаций, но и для линейных деформаций по любым трем взаимно перпендикулярным направлениям. В этом случае обобщенный закон Гука необходимо дополнить выражениями для угловых деформаций:

εx = Ε1 σx −µ(σy +σz ),

εy = Ε1 σy −µ(σx +σz ) ,

εz = Ε1 σz −µ(σx +σy );

γxy = τGxy ,

γyz = τGyz , (16.3)

γzx = τGzx .

Отметим, что для плоского напряженного состояния, например для случая σ3 = 0, из (16.2) будем иметь:

207

ε1 = Ε1 (σ1 −µσ2 ),

ε2 = Ε1 (σ2 −µσ1 ),

ε3 =−Εµ (σ1 +σ2 ).

Как видим, деформированное состояние при этом не является плоским.

Объёмная деформация

Найдем относительное изменение объёма элементарного параллелепипеда, показанного на рис. 16.1. До деформации элемент занимал объём V0 =dxdydz . Его объём после деформации

V=(dx+∆dx)(dy +∆dy)(dz +∆dz)=

=dx 1+∆dxdx dy 1+∆dydy dz 1+∆dzdz .

Учитывая (16.1), абсолютное изменение объёма можно представить в виде

∆V =V −V0 =dxdydz(1+ε1 )(1+ε2 )(1+ε3 )−dxdydz =

=V0 (ε1 +ε2 +ε3 +ε1ε2 +ε2ε3 +ε3ε1 +ε1ε2ε3 ).

Учитывая малость деформаций, их произведениями можно пренебречь, тогда получим

Величину θ называют объёмной деформацией, или относительным изменением объёма. Подставив в формулу (16.4) выраже-

ния деформаций из обобщенного закона Гука (16.2), будем иметь

208

Если ввести понятие среднего напряжения

σср =13(σ1 +σ2 +σ3 ),

то можно получить ещё одну форму записи закона Гука:

где K – модуль объёмной упругости, K =3(1−Ε2µ).

Из (16.6) следует, что при значении коэффициента Пуассона µ =0,5 объём тела при нагружении не изменяется. Примерами та-

ких несжимаемых материалов могут служить резина и парафин, а также сталь в состоянии температурной текучести.

Потенциальная энергия деформации

Потенциальной энергией деформации называют энергию, которая накапливается в теле при его статическом упругом деформировании. Поскольку при таком нагружении кинетическая энергия системы не меняется, а потери энергии в упругих материалах невелики, можно считать потенциальную энергию деформации численно равной работе внешних сил, совершённой ими при деформации тела.

Рассмотрим стержень с начальным поперечным сечением A и длиной l, растягиваемый медленно возрастающей силой F (рис. 16.2).

Если материал стержня подчиняется закону Гука, то зависимость нагрузки от удлинения линейна. Элементарная работа при изменении силы на величину dF, а удлинения – на величину d ∆l, равна произведению Fd ∆l, что соответствует на рис. 16.2 площади заштрихованной фигуры. Полная работа, совершаемая в процессе нагружения, представляет собой интегральную сумму таких элемен-

209

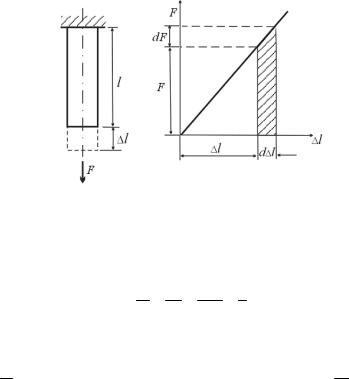
тарных площадей и равна площади треугольника, образованного диаграммой растяжения и горизонтальной осью:

Здесь W – работа внешней силы F на удлинении стержня ∆l; U – потенциальная энергия упругой деформации стержня.

Рис. 16.2.

Введём понятие удельной энергии деформации, разделив полную энергию U на объём стержня:

u = UV = UAl = F2Al∆l =12 σε ,

где σ – нормальное напряжение в поперечном сечении стержня,

σ= FA ; ε – соответствующая линейная деформация, ε=∆ll .

Обобщая полученный результат на случай объемного напряженного состояния, когда одновременно действуют все три главные напряжения, получим:

210