Оптимальное проектирование конструкций

где ρ g – удельный вес материала, из которого изготовлена ферма.

Обозначим через N1, N2, N3 усилия, которые возникают в стержнях при деформировании. Тогда, если предельное напряжение обозначить че-

рез σ 0 , то ограничения по напряжениям примут вид

Теперь в качестве переменных состояния удобнее взять перемещения ux, uy, тогда ограничения на перемещения примут вид

22

Запишем ограничения на устойчивости (при условии ux ≥ 0;u y ≥ 0 ):

го или прямоугольного), то ограничения по устойчивости можно записать в виде

Таким образом, задача свелась к определению трех чисел (s1, s2, s3), при которых критерий (1.3) минимален при выполнении ограничений (1.4, 1.8 и 1.9). Cформулированная задача является задачей нелинейного математического программирования.

Сделаем упрощение: пусть ферма – симметричная, т.е. s1 = s3. Тогда математическая формулировка оптимизационной задачи будет следующей: необходимо найти два таких значения s1 и s2 , чтобы

при ограничениях, которые можно записать сразу через переменные оптимизации, ибо система уравнений равновесия (1.7) легко может быть решена.

В этом случае ограничениями на перемещения (1.8) будут

23

Ограничением на перемещения является

у(х) ≤ у0.

Для записи ограничения на прочность воспользуемся положением сопротивления материалов о наибольших нормальных напряжениях, согласно которому прочность не нарушится, если справедливо соотношение

максимальный изгибающий момент, который можно определить из уравнения изгиба стержня

24

Если записать это уравнение в переменных прогиба, то оно примет вид

В отличие от предыдущего примера h(x) – функция, непрерывная или разрывная, а не конечномерный вектор переменных проектирования. Поэтому задачу оптимизации можно сформулировать как вариационную или как задачу управления. Однако данную задачу можно свести и к задаче математического программирования, если разбить стержень на ряд подобластей. В каждой подобласти толщина стержня постоянна (см. рис. 1.2).

Обозначим толщину стержня на i-м участке через hi (i = 1, 2, ..., n), n – число подобластей. Оптимизационную задачу тогда можно сформулировать следующим образом: найти такой n-мерный вектор h = (h1, h2, …, hn)т, чтобы критерий качества

здесь ( yi )max – максимальный прогиб на любом i-м участке, и ограничениях на прочность (1.16), которые должны выполняться на каждом участке,

(σ max )i = (M max )i hi ≤ σ 0 .

2(I x )i

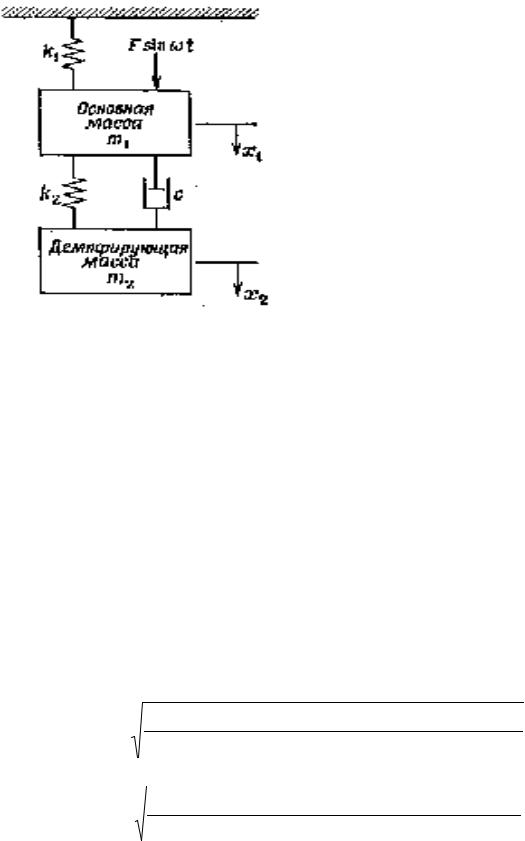
Пример 1.4. Оптимизация виброзащитных систем. Современные тенденции в проектировании ориентированы на создание гибких и легких конструкций, в которых при гармоническом воздействии могут возникать силы большой амплитуды, оказывая неблагоприятный эффект на функционирование и время жизни новой техники. Поэтому возникают задачи выбора параметров жесткости и демпфирования системы, чтобы минимизировать неблагоприятные эффекты гармонического отклика системы.

В большинстве практических ситуаций основная масса механизма может быть подвержена вибрации с большой амплитудой, в особенности,

25

стационарного процесса (ω = const) в качестве критерия качества можно взять отношение экстремального смещения основной массы к ее статическому смещению. Переходный процесс характеризуется конечным набором возмущающей силы.

Уравнения движения системы имеют вид

m1x1 +k1x1 + k2 (x1−x2 ) + c(x1 − x2 ) = F sin ω t, m2 x2 + k2 (x2 − x1) + c(x2 − x1) = 0,

где m1 и m2 – соответственно основная масса и масса гасителя; k1 и k2 – жесткости пружин; с – коэффициент демпфирования; F – амплитуда воздействующей силы; ω – частота возмущающей силы.

Амплитудное значение перемещений каждой из масс можно записать в виде [9]

26

новной системы.

Интенсивность вязкого трения характеризуется безразмерным параметром

µ= с m1 . 2m2 k1

Для данной задачи можно сформулировать несколько подзадач оптимального проектирования. Первоначально сформулируем оптимизационную постановку для стационарного случая, т.е. когда ω – постоянная величина.

Первая постановка: для заданного отношения масс β найти параметры гасителя k2 и с, минимизирующие отношение амплитудного зна-

Вторая постановка отличается от первой тем, что минимум отклика основной массы ищется в области значений возбуждающей частоты

ω min ≤ ω ≤ ω max .

Можно сформулировать оптимизационную задачу и для случая переходного процесса.

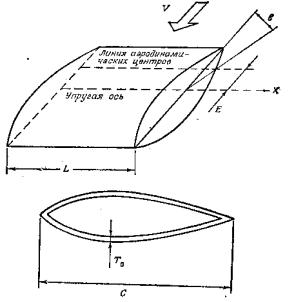
Пример 1.5. Проектирование прямоугольного крыла минимальной массы при заданной скорости дивергенции [1]. Рассмотрим консольное прямое крыло с упругой осью, перпендикулярной набегающему потоку. Предполагается, что профиль крыла не изменяется вдоль оси и характери-

зуется коэффициентом подъемной силы а0. Остальные параметры и обозначения приведены на рис. 1.4. Толщина T обшивки профиля переменна вдоль оси.

27

если ввести так называемое эталонное крыло с постоянной толщиной обшивки Т0, с таким же точно профилем и с той же скоростью дивергенции.

Задача оптимизации может быть поставлена следующим образом:

1

минимизировать функционал m = ∫ t(x)dx, представляющий безразмерную

0

массу обшивки, при ограничениях (1.18). Такая формулировка совпадает с принятой в теории оптимального управления.

28

2. ЗАДАЧИ ОДНОМЕРНОЙ МИНИМИЗАЦИИ

Современные оптимизационные задачи решаются с применением разнообразных алгоритмов. Анализ этих алгоритмов позволяет точно оценить их возможности и недостатки, а также рациональность применения на практике. Поэтому можно сказать, что знакомство с оптимизационными алгоритмами является необходимым (но не достаточным) условием исследования любой оптимизационной задачи. Начнем с задач безусловной оптимизации.

Для начала рассмотрим простейшие задачи, в которых изменяется только одна переменная. Это наиболее простой тип оптимизационных задач, что обусловлено следующим:

1)одномерные методы часто применяют для анализа подзадач, возникающих при использовании итерационных процедур решения оптимизационных задач большой размерности, например, для нахождения длины шага;

2)на этих задачах, как правило, идет разработка новых оптимизационных алгоритмов (удобная модель);

3)различные критерии и определения наиболее наглядны при рассмотрении функции одной переменной.

2.1. Определения и критерии оптимальности

Первоначально напомним некоторые определения. Если функция y = f (x) определена в любой точке множества всех действительных чисел,

то

y = f (x) , x S = R.

Если же x S, S = {x − 5 ≤ x ≤ 5 }, то f (x) определена в ограничен-

ной области. Область S называется областью допустимых значений. Следует всегда обращать внимание на характер зависимости функ-

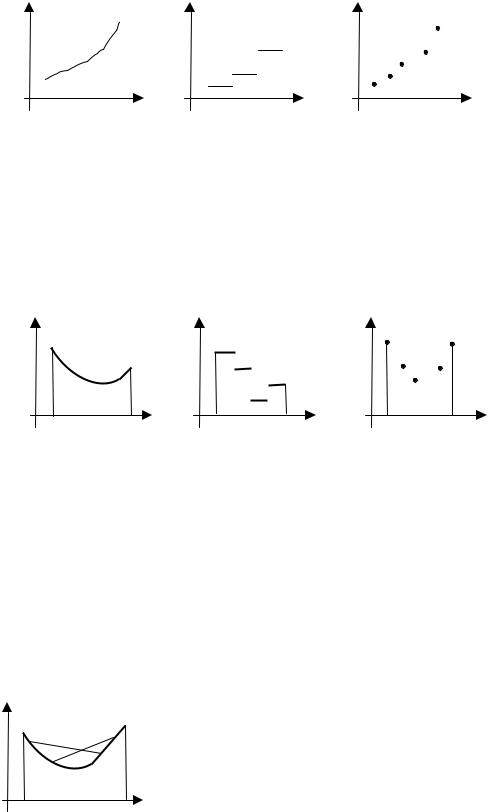
ции от аргумента, так как функции могут быть непрерывными (рис. 2.1, а), разрывными (рис. 2.1, б), переменные могут принимать только дискретные значения (рис. 2.1, в).

Наконец, функции можно классифицировать в зависимости от их формы:

1) монотонные функции: функция f (x) называется монотонной на некотором промежутке D, если для любых двух точек x1 и x2 при условии x1 < x2 выполняется одно из неравенств:

29

2) унимодальные функции: функция f (x) называется унимодальной на отрезке (a ≤ x ≤ b) , если она монотонна по обе стороны от единственной

на рассматриваемом отрезке точки x* , являющейся точкой минимума или максимума (рис. 2.2).

Из определения унимодальности функции не следует правила, по которому можно было бы проверить это свойство функции. Однако в оптимизационных задачах выделен довольно широкий класс функций (выпуклые или вогнутые), для которых это свойство легко проверяется.

Функция f(x) называется выпуклой тогда и только тогда, когда для

30