Вероятностные методы расчета конструкций

Решение уравнения (3.11) примет вид

y(x,t) k (x)(Ak cos pk t Bk sin pk t).

k 1

Константы Ak и Bk определяем из начальных условий. Воспользовавшись условием ортогональности собственных функций, будем иметь: A1 y0 , все остальные константы равны нулю, поэтому

y(x,t) y0 sin lx cos p1 t.

Математическое ожидание и корреляционная функция решения определяются выражениями:

3.2. Вынужденные линейные колебания систем

Случайные вынужденные колебания часто необходимо учитывать при расчете, например, транспортных средств при движении по неровной дороге или расчете летательных аппаратов с учетом действия атмосферной турбулентности, а также при расчетах высотных сооружений на действие ветра и т.д. Рассмотрим случайные колебания систем под действием случайных нагрузок, при этом под нагрузками будем понимать не только внешние силы, но и внешние кинематические воздействия (заданные перемещения системы или ее отдельных точек).

82

Если мощность воздействия достаточно велика по сравнению с мощностью возбуждаемого колебательного процесса, т.е. нагрузка пренебрежимо мало зависит от поведения системы, то такое воздействие называют стохастически заданным. Если, кроме того, нагрузки заданы в виде случайных функций времени, то описание таких нагрузок можно осуществить на основе теории случайных процессов.

В случайном процессе все характеристики колебаний, частоты и амплитуды параметров компонент можно определить, только обрабатывая обширный статистический материал. Следует отметить, что подготовительная работа по сбору необходимых сведений о случайных силах требует несоизмеримо больше времени, чем решение соответствующих уравнений. Например, сила, вызванная случайным ветром, зависит не только от скорости ветра, но и от формы обтекаемого тела. Однако в ряде случаев вероятностные характеристики сил, возбуждающих колебания, не зависят от самой конструкции и являются хорошо изученными случайными функциями. Это означает, что такие процессы можно оценивать на основе их временных детерминированных характеристик.

3.2.1. Системы с одной степенью свободы

Рассмотрим некоторые методы решения задач о вынужденных колебаниях линейных систем на простейшем примере системы с одной степенью свободы, колебания которой происходят в результате действия случайной нагрузки f (t). Уравнение

движения такой системы

эффициент сопротивления).

83

Первый способ решения состоит в использовании частного случая метода функций Грина – метода импульсных переходных функций. Для этого предполагаем, что в некоторый момент времени на систему действует единичный импульс, после чего развиваются колебания. Это означает, что необходимо найти решение задачи о свободных колебаниях при граничных усло-

виях: при t = ; x( ) = 0; x m1 . Это решение имеет вид:

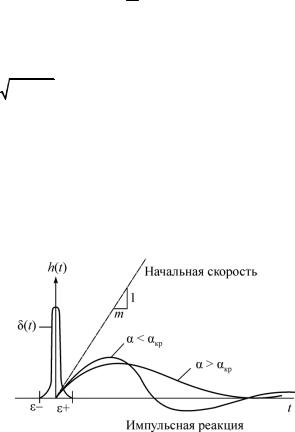
Определяемую при этом функцию h(t) (рис. 3.3) называют

импульсной переходной функцией, ибо она представляет собой реакцию предварительно невозбужденной системы на единичный мгновенный импульс. Очевидно, что реакция системы будет зависеть еще и от времени приложения импульса , а поэтому импульсная функция зависит от двух временных переменных, т.е. h(t, ) .

Рис. 3.3

Будем считать, что процесс на входе действует из бесконечно далекого прошлого (это означает, что можно не учиты-

84

вать начальные условия). Тогда, воспользовавшись интегралом Дюамеля и функцией h(t, ) , можно записать решение уравне-

ния (3.13) в следующем виде:

Особый интерес представляют стационарные системы. Для таких систем импульсная функция зависит явно только от разности ( t ), а формула (3.14) переписывается следующим образом:

Импульсная переходная функция зависит только от динамических свойств системы и не зависит от характера воздействия, а потому исчерпывающе характеризует динамическую систему. Зная вероятностные характеристики входа (математическое ожидание mf (t) и корреляционную функцию K f (t1,t2 ) ),

можно определить по соотношениям (2.7) и (2.8) вероятностные характеристики выхода:

mx (t) t mf ( )h(t, )d ,

0

t1 t2

Kx (t1,t2 ) h(t1, 1 )h(t2 , 2 )K f ( 1, 2 )d 1d 2 .

0 0

Если система является стационарной, то приходим к формулам:

mx (t) t mf ( )h(t )d ,

85

Учитывая конкретный вид импульсной функции (3.13), получим:

Если, наконец, внешнее воздействие является стационарным случайным процессом, тогда и поведение стационарной системы будет стационарным случайным процессом. Корреляционная функция в этом случае инвариантна относительно сдвига начального момента времени, а потому:

K f (t1,t2 ) K f (t1 t2 ); Kx (t1,t2 ) Kx (t1 t2 ).

Сделаем замену переменных:

Пусть для системы, движение которой описывается уравнением (3.15), корреляционная функция внешнего воздействия имеет вид

86

где K0 – постоянная.

Такое внешнее воздействие называется дельта-коррелиро- ванным и характеризует предельно широкополосный случайный процесс (белый шум), спектральная плотность мощности которого сохраняет постоянное значение на всех частотах. Таким образом, белый шум характеризуется тем, что его значения

влюбые два, даже сколь угодно близкие, момента времени некоррелированны. Следует отметить, что понятие белого шума относится только к спектральной картине случайного процесса и оставляет совершенно открытым вопрос о законах распределения. Точнее говоря, распределения вероятностей белого шума

вобычном смысле не существует. Белый шум является идеализацией (математической моделью), не реализуемой в действительных условиях, так как, во-первых, достаточно близкие значения случайного процесса практически всегда зависимы и, вовторых, реальные процессы имеют конечную мощность, а полная мощность белого шума бесконечна. Однако использование белого шума в качестве модели процессов на входе значительно упрощает математический анализ и не вносит сколько-нибудь существенных погрешностей.

Подставляя (3.19) в (3.18), получим:

а после вычисления интеграла будем иметь:

Таким образом, все вероятностные характеристики колеблющейся системы определены.

Другим способом отыскания решения является метод спектральных представлений. Как и прежде, ограничимся рассмот-

87

рением участков времени, достаточно удаленных от начала процесса, когда все переходные процессы в системе можно считать законченными и система работает в установившемся режиме.

В случае, когда воздействие f (t) представляет собой дос-

таточно простую аналитическую функцию, часто удается найти реакцию системы также в виде простой аналитической функции. В частности, когда воздействие представляет собой гармоническое колебание определенной частоты, система отвечает на него также гармоническим колебанием той же частоты, но измененным по амплитуде и фазе.

Поскольку координатные функции спектрального разложения стационарной случайной функции f (t) представляют собой

гармонические колебания заданной частоты , то задача решается очень просто, особенно если гармоническое колебание представлено в комплексной форме.

Пусть на вход системы (3.12) поступает гармоническое колебание вида

называется передаточной функцией.

Соотношение (3.21) может соответствовать нескольким видам возмущения в зависимости от значений А и s. Например:

f (t) ae nt , если s = –n; f(t) = A = const, если s = 0.

88

Если (3.21) подставить в уравнение движения (3.12), то можно найти выражение для передаточной функции:

Передаточная функция для простого гармонического колебания с частотой называется частотной характеристикой и получается подстановкой s = i в H(s):

Модуль Н называют амплитудно-частотной характеристикой. В частности, если f(t) = A sin t, то x(t) = B sin( t – ), здесь

Таким образом, если, например, на вход линейной системы с постоянными параметрами поступает гармоническое колеба-

ние вида ei t , то реакция системы представляется в виде того же гармонического колебания, умноженного на частотную характеристику системы H (i ) .

Пусть на вход системы поступает сила, спектральное разложение которой можно представить в виде:

k

где Uk – некоррелированные случайные величины, дисперсия Dk которых образует спектр случайной функции f (t) . В силу

линейности системы величина Uk выходит за знак оператора, и реакцию системы на воздействие (3.24) можно представить в виде спектрального разложения:

89

Найдем дисперсию комплексной случайной величины Wk :

D(Wk ) M Uk H (i k ) 2

Таким образом, при преобразовании стационарной случайной функции стационарной линейной системой каждая из ординат ее спектра умножается на квадрат модуля частотной характеристики системы для соответствующей частоты, т.е. при прохождении стационарной случайной функции через линейную стационарную систему ее спектр определенным образом перестраивается: некоторые частоты усиливаются, некоторые, напротив, ослабляются (фильтруются). Квадрат модуля частотной характеристики (в зависимости от k ) и показывает, как реагирует система на колебания

той или иной частоты. Очевидно, что спектральная плотность на выходе линейной системы получается из спектральной плотности

на входетемжеумножением на H (i ) 2 :

Таким образом, получили весьма простое правило: при преобразовании стационарной случайной функции стационарной линейной системой ее спектральная плотность умножается на квадрат модуля частотной характеристики системы. Дисперсия случайной величины на выходе находится по формуле (2.28):

Квадрат модуля частотной характеристики обладает весьма важным для практических расчетов свойством [15], которое заключается в том, что если затухание системы мало (мало сла-

гаемое 2in в (3.23)), то величина H (i ) 2 претерпевает значительные изменения только вблизи p0 , а на остальных частях

90