Вероятностные методы расчета конструкций

где постоянную А определяем из условия стыковки перемещений в точке С:

Максимальное напряжение будет в защемлении балки, поэтому:

где М – изгибающий момент; W – момент сопротивления сечения относительно главных осей.

1.2. Системы случайных величин

Первоначально рассмотрим наиболее простой случай – систему двух случайных величин Х, Y. Совместной функцией распределения двух случайных величин Х и Y называют вероятность совместного выполнения двух неравенств Х < x и Y < y, т.е.:

Двумерную плотность вероятности можно ввести по аналогии с одномерной, а именно:

21

f (x, y) 2 F(x, y) при F(x, y) x y f ( , )d d . (1.8)

Случайные величины Х и Y называются зависимыми, если события, заключающиеся в выполнении неравенств X < x и Y < y, зависимы друг от друга хотя бы при одной паре значений х и у. В этом случае плотности совместного распределения вероятностей системы двух случайных величин выражаются через одномерные и условные плотности следующим образом:

Случайные величины Х и Y называются независимыми, если события, заключающиеся в выполнении неравенств X < x и Y < y, независимы при любых значениях х и у. Для независимых случайных величин Х, Y совместная функция распределения (на основании правила умножения вероятностей независимых событий)

F(x, y) P(X x)P(Y y) или F(x, y) F1 (x)F2 ( y),

Пусть теперь одна случайная величина Y функционально связана с другой случайной величиной Х, т.е.

Относительно аргумента полагаем, что известна плотность распределения fx (x) или его интегральная функция распределения. Тогда плотность распределения [9]

где ( y) 1 ( y) x.

22

Например, решая задачу определения напряженно-дефор- мированного состояния конструкции в линейной постановке, мы имеем линейную зависимость между параметрами состояния (напряжениями или перемещениями) и нагрузкой. Тогда, зная вероятностные характеристики нагрузки, можно найти вероятностные характеристики параметров состояния.

Пример 1.2. Параметр состояния u связан с параметром нагрузки q линейно:

Считая известной плотность распределения нагрузки, определить плотность распределения параметра состояния.

Решение. Решая уравнение (1.13) относительно q, получим: q Ku ; dudq K1 . Если плотность распределения нагрузки fq (q) ,

то согласно соотношению (1.12)

Если распределение нагрузки можно описать, например, однопараметрическим распределением Рэлея (а – параметр распределения):

то распределение параметра состояния в случае линейной связи с параметром нагрузки примет вид:

23

т.е. получим опять распределение Рэлея:

где au Kaq .

Аналогично получаются выражения при описании других плотностей распределения при линейной связи случайных величин.

Рассмотрим теперь функцию z (x, y) двух случайных аргументов х и у. Тогда интегральная функция распределения

где f (x, y) – плотность совместного распределения вероятностей системы случайных величин х и у; D – область плоскости (х, у).

Плотность распределения вероятности величины z

24

Пусть, например, случайные величины х и у можно описать нормальным законом распределения и они независимы, т.е.

Тогда

Воспользовавшись табличными значениями для определенных интегралов и преобразуя полученное соотношение, получим:

Таким образом, если случайные величины x и y можно описать нормальным законом распределения, то и случайная величина z x у также распределена по нормальному закону.

Рассмотрим пример расчета конструкции, случайные характеристики которой описываются разными законами распределения.

25

Место приложения нагрузки также случайно и определяется равномерным законом:

1/ l, 0 x l; f (x)

0, x 0; x l.

Определить закон распределения изгибного момента в заделке, если нагрузка и координата ее приложения независимы.

Решение. Изгибной момент в заделке M = qx, следовательно, совместный закон распределения f(q, x) = f(q)f(x). Для определения закона распределения момента нужно учесть его область реализации. Для этого запишем функцию распределения момента и учтем для определения области интегрирования, что q = M/x. Тогда

26

С учетом этого при интегрировании по верхнему пределу получим:

d x f (t)dt f (x). dx

Для дальнейшего интегрирования снова сделаем замену:

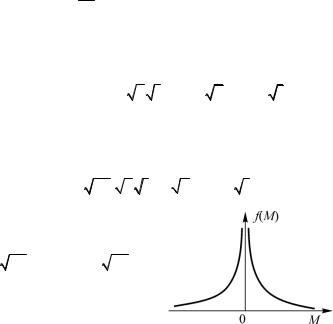
где I – интегральная показательная функция (при t > 0). Полученная функция f(М) имеет вид, показанный на рис. 1.5.

Таким образом, система случайных величин полностью определена, если известна совместная интегральная функция или совместная плотность распределения. Однако иногда, как уже отмечалось, бывает достаточно ограничиться их численными характеристиками.

1.3. Определение вероятностных характеристик элементов конструкций

Для системы из двух непрерывных случайных величин Х, Y имеем следующие числовые вероятностные характеристики:

27

Для установления связи между двумя случайными величинами вводится неслучайная числовая характеристика – корреляционный момент

Случайные величины называются некоррелированными, если их корреляционный момент равен нулю (например, корреляционный момент равен нулю для независимых случайных величин). Однако обратное утверждение в общем неверно: некоррелированные величины могут оказаться статистически зависимыми.

Корреляционный момент характеризует не только зависимость величин, но и их рассеяние. Если, например, одна из величин Х или Y мало отличается от своего математического ожидания, то корреляционный момент будет мал, какой бы зависимостью эти величины ни были связаны. Чтобы исключить этот момент, вводится безразмерная характеристика – коэффициент корреляции

где x , y средние квадратичные отклонения случайных вели-

чин Х и Y.

При практических расчетах коэффициент корреляции дает качественную информацию о взаимозависимости двух случайных величин. Например, если rxy > 0, то при возрастании одной

28

из случайных величин другая имеет тенденцию в среднем тоже возрастать, а при rxy < 0 при возрастании одной из случайных величин другая имеет тенденцию в среднем убывать.

Приведем числовые характеристики суммы и произведения двух случайных величин:

M[X Y ] M[X ] M[Y ];

Дисперсия произведения независимых случайных величин

Для центрированных случайных величин D(X Y ) Dx Dy .

Пример 1.4. Узел машины состоит из пяти деталей, собранных вместе таким образом, что их допуски суммируются. Необходимо, чтобы окончательный допуск для узла в собранном виде был равен ±0,25 мм. Примем, что для всех деталей допуски на обработку одинаковы и имеют независимые нормальные распределения. Необходимо найти допуск для детали, при котором обеспечивается требуемый допуск для узла.

Решение. Обозначим допуск для детали h . Поскольку допуски для отдельных деталей имеют нормальное распределение, то известно, что и допуск для всего узла будет также распределен по нормальному закону. Допустим, что все допуски соответствуют пределам 3 , т.е. среднее квадратичное отклонение размеров каждой детали равно h / 3 . Тогда среднее квадратичное отклонениеразмероввсегоузла составит / 3 . Витоге получаем:

29

Пример 1.5. При проектировании электрической цепи необходимо, чтобы ток находился в некоторых заданных пределах. Если предположить, что приложенное к цепи напряжение практически постоянно, то заданные пределы для тока должно обеспечить сопротивление R. Резистор R состоит из двух отдельных соединенных последовательно резисторов R1 и R2 со средним сопротивлением, равным 100 и 200 Ом соответственно. На основании исследования процесса изготовления известно, что сопротивление резисторов имеет нормальное распределение со средним квадратичным отклонением, равным 5 % от среднего значения сопротивления. Определить среднее значение полного сопротивления и его среднее квадратичное отклонение в двух случаях: а) резисторы независимы друг от друга; б) между резисторами существует корреляция, коэффициент которой равен – 0,7.

Решение. Среднее значение полного сопротивления

M[R] M[R1] M[R2] 100 200 300 Ом.

Если резисторы независимы, то

Таким образом, среднее квадратичное отклонение полного сопротивления составляет всего 3,73 % от среднего значения. Это значительно меньше значений среднего квадратичного отклонения для отдельных резисторов. Следовательно, последовательное соединение сужает допуски.

Если же допустить, что резисторы изготовляются на двух отдельных станках и их выбирают для сборки неслучайным образом (поэтому существует корреляция), то

R 2R1 2R2 2rR1R2 R1 R2

52 102 2 0,7 5 10 7,42 Ом.

В данном случае вследствие существования корреляции среднее квадратичное отклонение полного сопротивления составляет

30