Численный расчет стержневых систем

Другой способ получения связи между узловыми силами и узловыми перемещениями заключается в применении аналитического или численного интегрирования дифференциального уравнения, описывающего деформацию элемента; этот подход будет подробно рассмотрен применительно к изгибу бруса (см. подразд. 1.4).

Можно, наконец, с помощью известных методов сопротивления материалов найти сначала зависимость узловых перемещений от узловых сил, а затем обратить ее. Детали этого варианта описаны в подразд. 1.4.

1.2. Преобразование координат

Если, как говорилось выше, в качестве компонент матриц Pi , vi принять проекции сил и перемещений на координатные оси, то

элементы матрицы жесткости будут зависеть от принятой системы координат, выбор которой произволен. Для расчета конструкции применяют некоторую общую координатную систему. Однако для вычисления матриц жесткости отдельных конструктивных элементов может оказаться выгоднее воспользоваться местными системами координат. Для каждого конструктивного элемента местная система выбирается так, чтобы свести к минимуму вычислительную работу. В таких случаях после отыскания матрицы жесткости в местных координатах необходимо выполнить переход к общей системе координат.

Пусть x, y , z и x, y, z – соответственно местная и общая сис-

темы координатных осей. Тогда матрицы сил и узловых перемещений в местных и общих координатах обозначим соответственно так:

11

Количество элементов в подматрицах P1 , v1 или P1 , v1 определяется числом степеней свободы отдельного узла.

Выразим прежде всего v через v. Чтобы получить связь между перемещениями в двух системах координат, необходимо разло-

жить перемещение v по направлениям перемещений v. Если перемещения (линейные и угловые) типового узла i в общей системе координат спроектировать на местные координатные оси, то придем к соотношениям, которые в матричной форме имеют вид

где λ0 – матрица, составленная из косинусов углов между осями

x, y, z и x, y, z.

Подобные соотношения могут быть записаны для всех узлов рассматриваемого тела. Сведем их в одно матричное равенство:

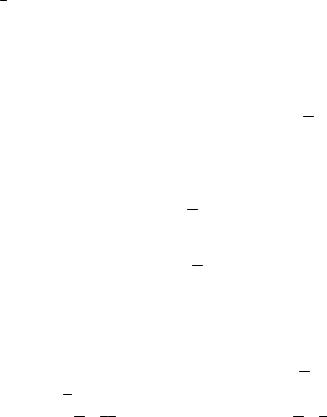
Матрица λ представляет собой матрицу преобразования координат. Отметим, что число диагональных блоков в формуле (1.6) равно числу узлов тела (или рассматриваемого конструктивного элемента).

Придадим далее точкам тела возможные перемещения и обо-

значим δv и δv матрицы-столбцы возможных перемещений узлов, отнесенных соответственно к местной и общей системам координат. На основании (1.7) эти матрицы связаны соотношением

Если узловые силы отнесены к местной системе координат, то на возможных перемещениях они произведут работу δv т P, если же

они отнесены к общей системе, то работа будет равна δvтP. Поскольку работа не зависит от того, в какой системе координат производятся вычисления, то

δvтP = δv т P.

Подставляя в это выражение формулу (1.8), получим:

δvтP = δvтλт P.

Отсюда в силу независимости элементов матрицы δv приходим к равенству

которое устанавливает связь между матрицами сил P и P.

Пусть, далее, k – матрица жесткости в местных координатах;

тогда согласно (1.2) P = kv. Учитывая (1.7), получим: P = kλv. Наконец, подстановка последнего равенства в (1.9) дает формулу

P = λтkλv.

Эта формула связывает силы и перемещения в общей системе координат в стандартной форме Р = kv.

13

координат известна, то для вычисления матрицы жесткости в общей системе достаточно построить матрицу λ и воспользоваться формулой (1.10). Матрица λ имеет вид (1.6), и задача сводится к составлению матрицы λ0 , конкретный вид которой зависит от того,

какие перемещения (степени свободы) узлов учитываются при расчете.

В качестве примера покажем составление матрицы λ0 для слу-

чая, когда в каждом узле рассматривается по три линейных перемещения в направлении координатных осей. На рис. 1.5 показаны проекции перемещения узла i на координатные оси двух систем – местной и общей.

Рис. 1.5

Обе матрицы v1 и v1 будут состоять здесь из трех элементов:

Обозначим λpg косинус угла между осью р ( p = x, y, z) мест-

Сопоставляя эту запись с (1.5), получаем:

λ0 x

λ0 = λ0 y . (1.12)

λ0 z

Заметим, что матрица λ имеет блочно-диагональный вид (1.6)

лишь в том случае, когда в матрицах v и v узловые перемещения перечисляются в одном и том же порядке:

v ={v1 v2 ... vm}т ; v ={v1 v2 ... vm}т .

При выводе матрицы жесткости в местных координатах иногда оказывается удобнее принять иной порядок расположения элемен-

15

сила Pi x , создающая такую деформацию, совпадает численно с ве-

а

б

в

Рис. 1.6

Воспользуемся далее известной из сопротивления материалов формулой ∆l = Pl / (EF ) для изменения длины стержня, нагруженного осевой силой P (здесь F – площадь поперечного сечения). Поскольку ∆l = vi x =1, P = Pi x = kii , то, подставив их в эту формулу, получим:

kii = EF / l.

Из условия равновесия стержня следует равенство Pj x = −Pi x ,

так что с учетом (1.13) имеем: k ji = −kii = −EF / l.

17

Аналогично рассмотрим деформирование стержня по схеме на рис. 1.6, в и получим k jj = −kij = EF / l.

Таким образом, матрица жесткости ферменного элемента в местной системе координат

i j

Здесь для определения указаны номера i, j строк и столбцов в со-

ответствии с порядком расположения элементов в матрицах P и v. Отнесем теперь ферменный элемент к общей системе коорди-

нат (рис. 1.7). Пусть ось стержня составляет с осями x, y, z углы, косинусы которых найдем по формулам:

Перемещение каждого узла имеет составляющие по всем трем осям общей системы координат, поэтому матрица vi перемещений узла i будет иметь три элемента:

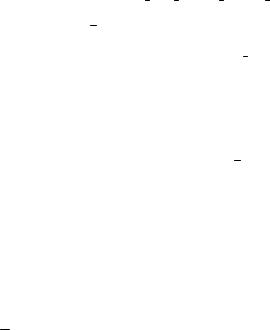
vi x = λxxvix +λxyviy +λxzviz .

Матрица vi перемещений узла i в местной системе координат состоит из единственного элемента vi x , поэтому последнее равен-

ство устанавливает требуемую связь между перемещениями узла i в местных и общих координатах. Если использовать матрицу

то оно примет стандартную форму v = λ0vi . Для стержня в целом получаем:

в общей системе координат и представим элементы матрицы в виде vi = λvi , где