
5617
.pdf
|
|
|
|
p 1 |
|
yt |
2 |
2 zt 1 |
( 2 j xt j 2 j yt j ) 2t , |
|
|
|
|
j 1 |
где zt yt xt |
|
M ( yt |
xt ) – стационарный ряд с нулевым математическим |
|
ожиданием, и |
2 |
2 |
0 . |
|
|
1 |
2 |
|
|
Известно, что в этом случае имеет место причинность по Гренджеру, по
крайней мере, в одном направлении. Значение |
xt 1 |
через |
посредство zt 1 |
|
помогает в прогнозировании значения |
yt (т.е. |
переменная xt является |
||
причиной по Гренджеру для переменной yt ), если |
2 |
0 . Значение yt 1 через |
||
посредство zt 1 помогает в прогнозировании значения |
xt (т.е. переменная yt |
|||
является причиной по Гренджеру для переменной xt ), если 1 |
0 . |
|||
При коинтегрированности I(1)-рядов xt , yt имеем: |
|
|
||
модель долговременной (равновесной) связи yt |
xt |
; |
||
модель краткосрочной динамики в форме ECM, |
|
|
||
и эти модели согласуются друг с другом. |
|
|
|
|
Приведём двухшаговую процедуру |
построения |
ЕСМ, |
предложенную |
|
Энглом и Гренджером для нестационарных временных рядов. |
|
||
На первом шаге значения параметров |
и |
модели yt |
xt t |
оцениваются обычным МНК и затем находятся оценённые значения
отклонений от положения равновесия t = yt – |
– xt как остатки от |
оценённой регрессии. |
|
На втором шаге МНК раздельно оцениваются уравнения (3.1), (т.е. предполагается VAR(p) модель для xt , yt ). При этом, МНК-оценки стандартных ошибок всех оценок параметров модели являются состоятельными. Проблемы же, возникающие на первом шаге (суперсостоятельность оценок), не являются значимыми, т.к. этот шаг является вспомогательным, зато на втором шаге можно пользоваться обычными статистическими процедурами.
При практическом применении двухшаговой процедуры Энгла– Гренджера ряд остатков  t = yt –
t = yt – 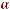 –
–  xt, полученных на первом шаге, используется не только для оценки ЕСМ на втором шаге, но и для проверки гипотезы о некоинтегрируемости рядов xt и yt . При этом надо иметь в виду,
xt, полученных на первом шаге, используется не только для оценки ЕСМ на втором шаге, но и для проверки гипотезы о некоинтегрируемости рядов xt и yt . При этом надо иметь в виду,
что тестируется не «сырой» временной ряд, а ряд остатков, полученных после оценивания модели.
71

Приведём пример оценки ЕСМ-модели с исходными данными, приведёнными на рисунке 3.4.
Модель коррекции остатков будем строить для р = 2. В общем случае этот показатель определяется из дополнительных исследований. В соответствии с первым шагом двухшаговой процедуры Энгла – Гренджера
оценим |
параметры |
уравнения |
долгосрочной связи между этими |
|
показателями в виде yt |
xt t |
(рисунок 3.5). |
||
|
|
|
|
|
Рисунок 3.5 – Уравнение регрессии равновесной связи
Получили: CSt = –192,98 + 0,7056 GDPt + et, так что zt = et = CSt + 192,98 – 0,7056 GDPt.
Рисунок 3.6 – ADF-тест остатков уравнения равновесной связи
Тест на единичный корень (рисунок 3.6) показал, что остатки et вроде нестационарны (гипотеза о единичном корне отклоняется, Prob. = 0,0385).
Но не следует забывать, что мы тестируем не «сырой» временной ряд, а оценённые остатки, а для них, как отмечалось ранее, критическое значение
72
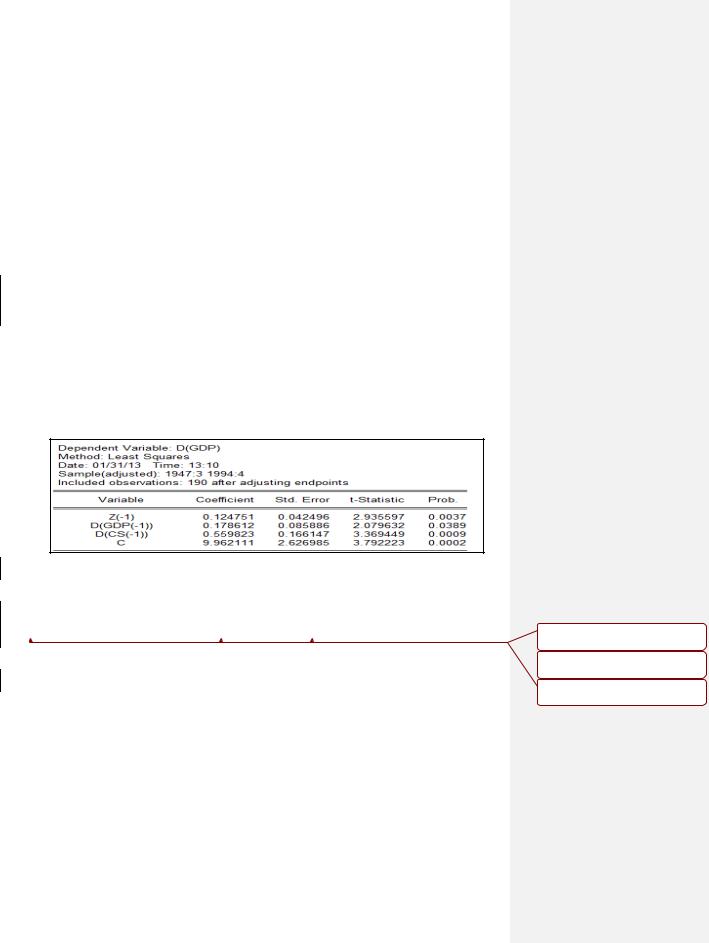
DF-t-статистики равно –3,34. А расчётное значение этой статистики равно
–2,98, что правее приведённого критического значения. Следовательно, на 5%-ном уровне значимости будем считать, что анализируемые ряды коинтегрированы. Хотя здесь не всё так просто. Например, на основе статистики Дарбина – Уотсона можно сделать вывод, что остатки нестационарны. Но абстрагируемся от этого и будем считать, что можно строить модель коррекции ошибок (остатков).
Модель коррекции остатков в наших предположениях будет строить в виде
 GDPt = µ1 + α1 zt-1 + γ11
GDPt = µ1 + α1 zt-1 + γ11 GDPt-1 + γ12
GDPt-1 + γ12 CSt-1 + e1t,
CSt-1 + e1t,
 CSt = µ2 + α2 zt-1 + γ21
CSt = µ2 + α2 zt-1 + γ21 GDPt-1 + γ22
GDPt-1 + γ22 CSt-1 + e2t.
CSt-1 + e2t.
Сначала оценим отдельно уравнение для GDPt. Для этого сохраним остатки уравнения равновесной связи под именем zt , а уравнения для GDPt
будем специфицировать в виде: d(GDP) z(–1) d(GDP(–1)) d(CS(–1)) c.
Итак, для первого уравнения получим (рисунок 3.7)
Рисунок 3.7 – Оценка уравнения регрессии для  GDPt
GDPt
Таким образом, оценённое уравнение регрессии для  GDPt примет вид
GDPt примет вид
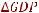 t = 9,96 + 0,125zt-1 + 0,18
t = 9,96 + 0,125zt-1 + 0,18 GDPt-1 + 0,56
GDPt-1 + 0,56 CSt-1.
CSt-1.
Все его оценки статистически значимы.  Оценим уравнение регрессии для
Оценим уравнение регрессии для  CSt. Его спецификация следующая:
CSt. Его спецификация следующая:
d(CS) z(–1) d(GDP(–1)) d(CS(–1)) c. Оценка «полного» уравнение имеет вид (рисунок 3.8).
Отформатировано: английский
(США)
Отформатировано: английский
(США)
Отформатировано: английский
(США)
73

Рисунок 3.8 – Оценка «полного» уравнения регрессии для  CSt
CSt
Удалив из этого уравнения незначимые члены с наибольшими значениями Prob., получили (рисунок 3.9).
Рисунок 3.9 – Оценка сокращённого уравнения регрессии для  CSt
CSt
Удалив незначимый член D(CS(–1)), окончательно получим.
Рисунок 3.10 – Оценка уравнения регрессии для |
CSt со значимыми |
|
|
членами |
|
|
|
Таким образом, оценённое уравнение регрессии для |
CSt (рисунок 3.10) |
|
|
примет вид |
|
|
|
t = 12,02 + 0,13 |
GDPt-1. |
|
|
Итак, получили следующую ЕСМ: |
|
|
|
t = 9,96 + 0,125zt-1 + 0,18 |
GDPt-1 + 0,56 CSt-1. |
|
|
t = 12,02 + 0,13 |
GDPt-1. |
|
|
Получили, что коррекция производится только в отношении ряда GDP: |
|
||
при положительных отклонениях от равновесного состояния, т.е. при GDPt-1 |
|
||
> 281,1 + 1,41CSt-1, в правой части уравнения для |
t корректирующая |
Отформатировано: русский |
|
|
|
|
|
74 |
|
|
|

составляющая zt-1 – положительная и с учётом знака перед ней действует в сторону уменьшения приращения переменной GDPt. И наоборот, при отрицательных zt-1 корректирующая составляющая действует в сторону увеличения приращения переменной GDPt.
Прошлые значения переменной CSt через посредство zt-1 помогают в прогнозировании значения GDPt т.е. переменная CSt является причиной по Гренджеру для переменной GDPt. В то же время прошлые значения переменной GDPt не помогают прогнозированию значения CSt, так что GDPt не является причиной по Гренджеру для переменной CSt.
Таким образом, получили, что в анализируемом периоде совокупное потребление страны зависит от динамики валового национального продукта, но не наоборот.
Рассчитаем модель коррекции остатков в автоматизированном режиме, используя возможности эконометрического пакета EViews (рисунок 3.1).
Рисунок 3.11 – Отчёт об оценивании ECM в пакете EViews
Получили несколько иные результаты, т.к. здесь не предусмотрена возможность пошагово избавляться от незначимых слагаемых в уравнениях модели коррекции остатков.
75

Глава 4. Панельные данные
4.1. Основные понятия
Панельные данные представляют собой информацию, собранную для разных объектов наблюдения в последовательные промежутки времени. Это, по сути дела, – смесь пространственной информации и временных рядов. Применение таких наблюдений позволяет специфицировать и оценивать более сложные и более реалистические модели, чем применение одной пространственной выборки или одного временного ряда.
В панельных данных повторно наблюдаются одни и те же объекты, поэтому различные наблюдения могут быть зависимыми. Это усложняет анализ, что требует применения специальных методов оценки параметров моделей панельных данных.
Поскольку совокупности панельных данных, как правило, обширнее, чем совокупности пространственных данных или совокупности данных одномерных временных рядов и объясняющие переменные изменяются в двух измерениях (время и объекты), то оценки, построенные на основе панельных данных, часто точнее, чем те, которые построены на основе одномерных источниках данных.
Обычно множество панельных данных состоит из наблюдений за большим числом объектов в течение небольшого числа периодов, и потому при их анализе больше внимания уделяется моделированию различий между объектами, чем анализу эффектов во времени. Но, несмотря на то, что временные эффекты в явном виде не моделируются, панельные данные содержат информацию относительно развития объектов во времени. И во многих случаях подобную информацию можно проанализировать только на основе панельных данных.
Кроме того, панельные данные позволяют снизить эффект смещения оценок параметров модели из-за невключения в модель значимых переменных. Дело в том, что на основе панельных данных можно уловить эффект неоднородности объектов, т.е. эффект всех переменных (в том числе и ненаблюдаемых), который не изменяется во времени. Добиться этого можно, введя в модель специфический эффект объекта и рассматривать его в качестве фиксированного неизвестного параметра. Таким образом, оценки, построенные по совокупности панельных данных, могут быть более устойчивыми к неполной спецификации модели.
76

Переменные в панельных данных имеют двойной индекс: i – для объектов (i= 1,2,…,n) и t – для периодов времени (t = 1,2,…,T). В общем виде линейную модель панельных данных можно записать так:
yit = |
βit + εit, |
где вектор коэффициентов βit |
измеряет частные эффекты вектора |
объясняющих переменных xit в период t для объекта i. Такая модель является слишком общей и не подлежит оцениванию. Будем предполагать, что вектор коэффициентов βit не зависит ни от времени, ни от объектов, за исключением свободного члена. Такую модель можно записать как
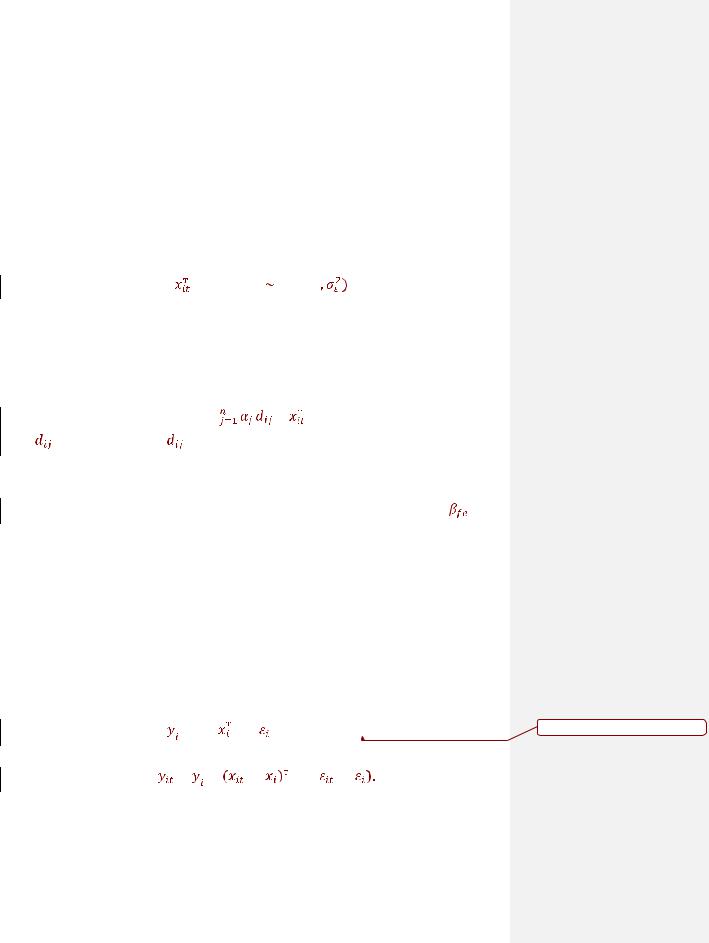
yit = αi + 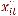 β + εit,
β + εit,
где xit – вектор независимых переменных, не включающий константу. Эта модель означает, что влияние независимых переменных на зависимую одинаково для всех i и t, но средний уровень каждого объекта отличается от среднего уровня для другого объекта. Таким образом, коэффициенты αi улавливают эффекты тех переменных, которые являются специфическими для i-го объекта, и которые являются постоянными во времени. В стандартном случае предполагается, что остатки εit являются независимыми и одинаково распределёнными по i и t с нулевым средним и дисперсией 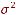 . Если коэффициенты αi рассматривать как фиксированные неизвестные параметры, то эта модель называется стандартной моделью с фиксированными эффектами.
. Если коэффициенты αi рассматривать как фиксированные неизвестные параметры, то эта модель называется стандартной моделью с фиксированными эффектами.
Другой подход предполагает, что свободные члены объектов различны, но их можно рассматривать как извлечения из распределения со средним µ и дисперсией 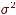 . Существенным предположением здесь является то, что эти извлечения не зависят от объясняющих переменных xit. Это приводит к модели со случайными эффектами, где индивидуальные эффекты αi рассматриваются как случайные (в смысле случайной выборки). Член отклонения в этой модели состоит из двух компонент – не зависящей от времени компоненты αi и остаточной компоненты εit, которая не коррелирована во времени (без автокорреляции). Такую модель можно записать как
. Существенным предположением здесь является то, что эти извлечения не зависят от объясняющих переменных xit. Это приводит к модели со случайными эффектами, где индивидуальные эффекты αi рассматриваются как случайные (в смысле случайной выборки). Член отклонения в этой модели состоит из двух компонент – не зависящей от времени компоненты αi и остаточной компоненты εit, которая не коррелирована во времени (без автокорреляции). Такую модель можно записать как
yit = µ + 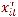 βit + αi + εit,
βit + αi + εit,
где µ – свободный член.
77
Большинство моделей панельных данных оценивается либо в предположении фиксированных эффектов, либо в предположении случайных эффектов. Рассмотрим их подробнее.
4.2. Модель с фиксированными эффектами
Модель с фиксированными эффектами является линейной моделью регрессии, в которой свободные члены изменяются при переходе от одного
объекта к другому, т.е. |
|
|
|
yit = αi + β + εit, |
εit НОР(0 |
, |
(4.1) |
причём предполагается, что все εit |
независимы |
от |
всех xit (это одно из |
важнейших предположений модели с фиксированными эффектами). |
|||
Параметры этой модели можно оценить по-разному. Один из вариантов |
|||
оценки предполагает записать эту модель с использованием фиктивных переменных для каждого объекта. Тогда модель примет вид
|
|
yit = |
+ β + εit, |
где |
= 1, если i = j, и |
= 0 |
в противном случае. Параметры этой модели |
(α1,…, αn и β) можно оценивать с помощью обычного МНК. В этом случае оценка вектора неизвестных параметров β называется оценкой метода
наименьших квадратов с фиктивными переменными и обозначается |
(fixed |
effects). Недостаток подобного метода оценивания заключается в |
|
необходимости оценивать большое число параметров (n параметров αi и k |
|
параметров β). Однако этот недостаток можно преодолеть, применив другой |
|
метод оценивания. Можно показать, что точно та же самая оценка для |
|
||||||||||||||||||
вектора β получается, если регрессия строится в отклонениях от |
|
||||||||||||||||||
индивидуальных средних. Для этого с помощью преобразования данных |
|
||||||||||||||||||
сначала исключаются индивидуальные эффекты αi. С этой целью в исходном |
|
||||||||||||||||||
уравнении все переменные усредняются по времени, в результате чего |
|
||||||||||||||||||
получаем |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
= αi + |
β + . |
(4.2) |
Отформатировано: русский |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Вычтем из уравнения (4.1) уравнение (4.2) и получим |
|||||||||||||||||||
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
β +( |
|
|
|
|
|
||||||
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
||||||||||||
Получили модель регрессии в отклонениях от индивидуальных средних, |
|
||||||||||||||||||
которая не включает индивидуальные эффекты αi. Такое преобразование |
|
||||||||||||||||||
называется внутригрупповым |
(внутриобъектным) преобразованием. А |
|
|||||||||||||||||
78
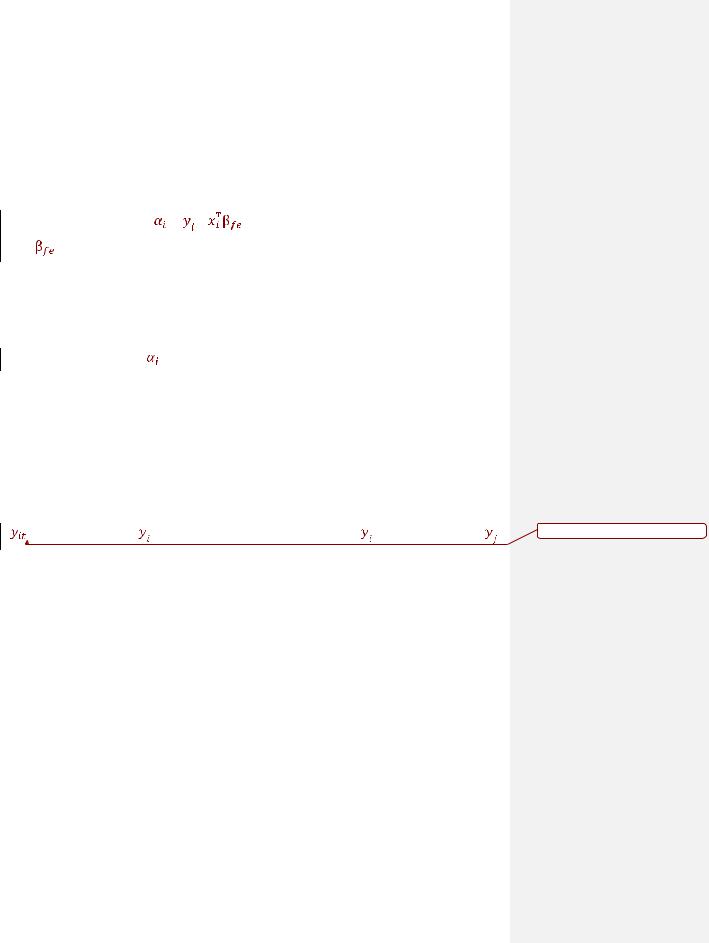
оценку для вектора неизвестных параметров β, полученную из этой |
|
||||||||||||||
преобразованной модели, называют внутригрупповой оценкой или оценкой с |
|
||||||||||||||
фиксированными эффектами, и она в точности идентична оценке, |
|
||||||||||||||
полученной по модели с фиктивными переменными. |
|
|
|
|
|
|
|||||||||
|
Если объясняющие переменные не зависят от всех остатков, то |
|
|||||||||||||
индивидуальные эффекты можно оценить из уравнения (4.2): |
|
|
|
||||||||||||
|
|
|
|
= |
|
- |
|
, |
(i = 1,…,n), |
(4.3) |
|
|
|
||
|
|
|
|
|
|
|
|
|
|||||||
где |
оценивается по модели регрессии в отклонениях от индивидуальных |
|
|||||||||||||
средних. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Следует иметь в виду, что оценивание эффектов по (4.3) (с помощью |
|
|||||||||||||
внутригруппового преобразования) хоть и позволяет получить более |
|
||||||||||||||
эффективные оценки вектора параметров β, но не позволяет определить |
|
||||||||||||||
значимость оценок , как если бы они были получены из модели с |
|
||||||||||||||
фиктивными переменными. Хотя многие исследователи отмечают, что |
|
||||||||||||||
численные значения этих оценок (при больших выборках) мало |
|
||||||||||||||
информативны и в анализе обычно не участвуют. Здесь важно определить, |
|
||||||||||||||
значимо ли они различаются, т.е. есть ли индивидуальные различия? А для |
|
||||||||||||||
этого есть специальные тесты. |
|
|
|
|
|
|
|
|
|||||||
|
По существу, модель с фиксированными эффектами описывает различия |
|
|||||||||||||
между объектами («внутри» объектов). Т.е. объясняет, до какой степени |
|
||||||||||||||
отличается от |
|
но |
|
не |
объясняет, почему |
|
|
отличается от |
|
. |
Отформатировано: русский |
||||
|
, |
|
|
|
|
||||||||||
Интерпретируя результаты для регрессии с фиксированными эффектами |
|
||||||||||||||
необходимо иметь в виду, что параметры идентифицируются только через |
|
||||||||||||||
внутрииндивидуальную (или, что то же, внутригрупповую) размерность |
|
||||||||||||||
данных. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Поскольку модель с фиксированными эффектами – это простая |
|
|||||||||||||
регрессионная модель, оценки параметров можно тестировать с помощью |
|
||||||||||||||
обычных t- и F-тестов. Один из вопросов, который интересует исследователя |
|
||||||||||||||
в отношении параметров модели с фиксированными эффектами: значимо ли |
|
||||||||||||||
различаются эффекты, |
характерные |
для отдельных объектов наблюдения, |
|
||||||||||||
т.е. значимо ли различаются параметры αi для разных объектов наблюдения? Этот вопрос ещё называют вопросом объединения, поскольку если эффектов, специфических для отдельных объектов, нет, все данные могут быть объединены в одну простую регрессию с единственной константой.
79

Для ответа на этот вопрос формулируют нулевую гипотезу о том, что αi = αj для любых i,j, что соответствует модели с одним и тем же параметром α для всех объектов наблюдения. Такую модель называют объединённой моделью (pooled).
yit = α +  β + εit.
β + εit.
Альтернативная гипотеза формулируется так: не все αi равны, т.е. хотя бы
для одной пары i,j αi |
αj, что соответствует модели с фиксированными |
||||||||||||
эффектами. Проверяется эта гипотеза с помощью F-теста (Вальда). |
|||||||||||||
|
F = |
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
||||||||
где k – размерность вектора β.
Если верна нулевая гипотеза (индивидуальные эффекты не различаются, т.е. мы имеем объединённую модель), и выполняется предпосылка о нормальном распределении остатков, то F-статистика имеет (приближённо) распределение Фишера. Если F-расч. > F-табл., то нулевая гипотеза отклоняется, и мы имеем модель с фиксированными эффектами.
Отметим недостатки модели с фиксированными эффектами. Если оценивать её параметры, используя фиктивные переменные, то ввиду большого числа оцениваемых параметров такие оценки могут быть неэффективными (теряются степени свободы регрессии). Если оценивать её параметры с помощью двухшаговой процедуры, т.е. сначала на основе уравнения в отклонениях от средних оценить вектор параметров β, а затем из уравнения (4.3) индивидуальные эффекты αi, то в этом случае не будут учитываться факторы, не меняющиеся во времени, поскольку для них отклонения от средних будут равны нулю. Подобного недостатка лишена модель со случайными эффектами.
4.3.Модель со случайными эффектами
Врегрессионном анализе обычно предполагается, что все факторы, которые влияют на зависимую переменную, но не вошли в модель в качестве регрессоров, могут в итоге суммироваться в случайном остаточном члене уравнения. В случае панельных данных это приводит к предположению, что эффекты αi являются случайными факторами, независимо и одинаково распределёнными по объектам. В этом случае модель случайных эффектов может быть записана в виде
80
