
5617
.pdf
Пусть известно, что yt и xt являются I(1), и предположим, что оценивается коинтегрирующая регрессия
yt = α + βxt + εt. |
|
(2.12) |
|
Если yt и xt коинтегрированы, то член оценённой ошибки в регрессии |
|
||
(2.12) является I(0), в противном случае et будет I(1). Следовательно, можно |
|
||
протестировать наличие коинтегрирующего соотношения с помощью теста |
|
||
наличия единичного корня в оценённых остатках et из регрессии (2.12). |
|
||
Однако следует иметь в виду, что этот случай теста наличия единичного |
|
||
корня несколько отличается от обычного тестирования временного ряда на |
|
||
единичный корень. Дело в том, что здесь тестируются остатки, полученные |
|
||
методом наименьших квадратов. А метод наименьших остатков |
|
||
минимизирует дисперсию остатков. Поэтому он выбирает среди всех |
|
||
остатков те, которые имеют минимальные значения по абсолютной |
|
||
величине. И даже если остатки нестационарны, то данный метод делает их |
|
||
похожими на стационарные, и мы в этом случае можем отклонять гипотезу о |
|
||
единичном корне (о нестационарности) слишком часто. |
|
|
|
Чтобы избежать подобных ошибок, были вычислены соответствующие |
|
||
критические значения, отличные от стандартных критических значений |
|
||
теста Дики – Фуллера. Так, например, асимптотическое критическое |
|
||
значение теста наличия единичного корня в остатках для коинтеграции (с |
|
||
константой) на 5%-ном уровне значимости равно –3,34, вместо –2,86 в |
|
||
стандартном случае. |
|
|
|
Другой метод тестирования коинтеграции основан на статистике Дарбина |
|
||
– Уотсона, рассчитанной для исходного уравнения. В этом случае |
|
||
проверяется гипотеза о равенстве нулю статистики Дарбина – Уотсона для |
|
||
генеральной совокупности. Это связано с тем, что, как известно, связь между |
|
||
статистикой Дарбина – Уотсона (dw) и коэффициентом автокорреляции |
|
||
остатков первого порядка (ra(1)) определяется соотношением dw |
2(1– ra(1)). |
Отформатировано: русский |
|
Поэтому, если ra(1)) =1 (единичный корень), то dw |
. Этот тест называется |
|
|
тестом коинтегрирующей регрессии Дарбина – Уотсона.
В эконометрической литературе приводятся критические значения этой статистики для разных уровней значимости (для 5%-ного уровня значимости, например, критическое значение равно 0,386, если число наблюдений равно 100 и равно 0,2 при числе наблюдений, равном 200). Если расчётное значение статистики Дарбина – Уотсона превышает критическое значение, то гипотеза об отсутствии коинтеграции отклоняется.
61

Известно, что если ряды коинтегрированы, то существует адекватное представление коррекции остатков для данных. Таким образом, если оба ряда yt и xt являются I(1), и имеют коинтегрирующий параметр β, то существует представление коррекции остатков zt = yt – α – βxt вида
yt = δ xt-1 – γ(yt-1 – α – βxt-1) + εt.
Это означает, что если оба ряда yt и xt являются I(1), но имеют долгосрочное динамическое соотношение, то должна быть некоторая сила, которая возвращает ошибку равновесия к нулю. И эта модель описывает, как yt и xt ведут себя в краткосрочной динамике в соответствии с долгосрочным динамическим коинтегрирующим соотношением. Если параметр коинтеграции известен, то все члены модели коррекции остатков являются I(0) и эту регрессию можно оценить с помощью обычного метода наименьших квадратов. Если параметр β неизвестен, то его можно оценить (супер) состоятельно из коинтегрирующей регрессии (2.12) и применить обычную технику оценивания параметров модели коррекции остатков.
Необходимо иметь в виду, что здесь рассмотрен простейший вариант модели коррекции остатков. Кроме того, известно, что если оба ряда yt и xt являются I(1) и имеют представление коррекции остатков, то они обязательно коинтегрированы. Важно уяснить, что понятие коинтеграции можно применить только к (нестационарным) интегрированным временным рядам.
Рассмотрим пример анализа временных рядов на коинтеграцию. Пусть рассматриваются два временных ряда (cpr и tbr), графики которых изображены в левой части рисунка 2.8. Чтобы проверить эти ряды на коинтеграцию, сначала надо проверить, что они являются I(1). Проверка показала (здесь не приводится), что они являются I(1). Построим коинтегрирующую регрессию (рисунок 2.8 – правая часть). Уже на основе статистики Дарбина – Уотсона можно было бы сделать вывод о том, что остатки этой регрессии стационарны (хотя и являются автокоррелированными). Но проведём дополнительный анализ остатков на стационарность на основе теста на единичный корень.
62
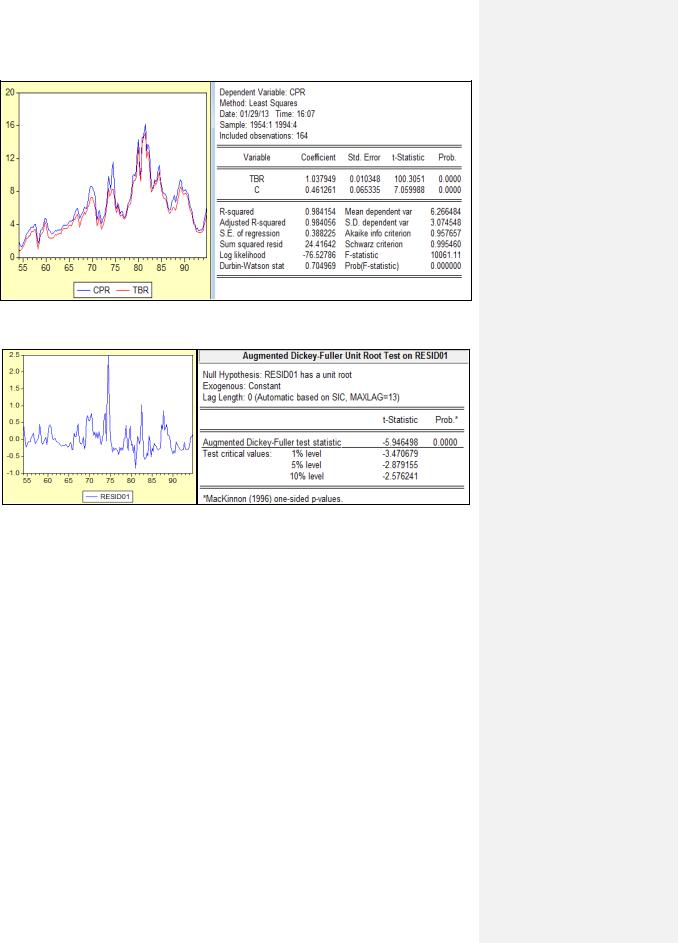
Рисунок 2.8 – Коинегрирующая регрессия
Рисунок 2.9 – Тест на единичный корень остатков коинтегрирующей регрессии
На рисунке 2.9 слева изображён график остатков регрессии, а справа – тест на единичный корень. Гипотеза о единичном корне отклоняется (Prob. для t-статистики равна 0,00), следовательно, остатки регрессии являются I(0) и анализируемые ряды коинтегрированы.
Приведём оценку модели коррекции остатков. В нашем случае она примет вид cprt = δ tbrt-1 – γ (cprt-1 – α – β tbrt-1). Обозначив остатки коинтегрирующей регрессии через z, специфицируем эту модель так: d(cpr) d(tbr(–1)) z(–1). После оценивания получим (рисунок 2.10)
63

Рисунок 2.10 – Оценка модели коррекции остатков
С учётом того, что корректирующий коэффициент получился отрицательным (γ = –0,65), коррекция остатков по направлению совпадает со знаком остатков: при отрицательных остатках коррекция осуществляется со знаком минус и наоборот.
Глава 3. Векторные модели авторегрессии
3.1. Общие положения
Векторная модель авторегрессии описывает динамическое развитие нескольких переменных на основе их общей истории, т.е. это такая модель, в которой изучаются несколько зависимых переменных, зависящих от собственных лагов и от лагов других переменных. Наибольший порядок запаздываний, включаемых в модель, называется порядком векторной авторегрессии. Если этот порядок равен р, то для такой модели используют обозначение VAR(p).
Векторные модели авторегрессии (Vector Autoregression – VAR) можно рассматривать как некий гибрид моделей одномерных временных рядов и систем одновременных уравнений. При их применении не приходится решать вопросы отнесения той или иной переменной к эндогенным или экзогенным переменным, что порой не совсем просто. Кроме того, эти модели позволяют исследовать зависимости с более сложной структурой, чем в анализе одномерных временных рядов или с использованием более сложных систем одновременных систем уравнений, что во многих случаях обеспечивает более высокое качество прогнозов.
К недостаткам VAR-моделей можно отнести неопределённость в выборе подходящей длины лага, значительное число оцениваемых параметров и то,
64

что все переменные в модели должны быть стационарными. Данные проблемы решаются дополнительными исследованиями (имитационное моделирование, преобразование переменных и т.п.).
Рассмотрим частный случай, когда рассматриваются две переменные и зависят они от лаговых значений этих переменных до второго порядка включительно. Такая модель (VAR(2)) имеет вид
y1t |
10 |
11 y1t 1 |
12 y1t 2 |
11 y2 y 1 |
12 y2t 2 |
1t , |
y2t 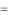 20
20  21 y2t 1
21 y2t 1 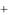 22 y2t 2
22 y2t 2  21 y1y 1
21 y1y 1  22 y1t 2
22 y1t 2 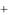 2t ,
2t ,
где 1е и 2е – два процесса белого шума (независимые от истории у и х),
которые могут быть коррелированы. Называются они по-разному: инновации, шоки, импульсы. Оценивают параметры таких моделей обычным МНК, применяемым к каждому уравнению отдельно.
Запишем эту модель в матричном виде, введя обозначения
|
Y |
y1t , |
10 |
, |
|
11 |
11 , |
|
|
12 |
12 |
, |
|
|
|
|
t |
y2t |
|
|
1 |
|
|
2 |
|
|
|
|
|
|
|
|
|
20 |
|
21 |
21 |
|
|
22 |
22 |
|
|
|
|
||
|
|
Y |
Y1t 1 , Y |
Y1t 2 , |
t |
1t . |
|
|
|
|
|
||||
|
|
t 1 |
Y2t |
|
t 2 |
Y2t 2 |
|
|
|
|
|
|
|
||
|
|
|
1 |
|
|
2t |
|
|
|
|
|
|
|||
Получим |
Yt |
1Yt 1 |
|
2Yt 2 t |
|
или |
Yt |
|
1Yt |
1 |
2Yt 2 |
0 |
|
t . |
|
Последнее выражение можно представить как ( |
1 |
L |
2 |
L2 )Y |
0 |
t |
, |
где |
|||||||
|
|
|
|
|
|
|
|
|
t |
|
|
||||
L – лаговый оператор.
Известно, что условием стабильности такой модели является тот факт,
что все обратные корни |
уравнения |
det ( z |
1 |
z 2 |
) 0 лежат за |
|
|
|
2 |
|
пределами единичного круга, т.е. их модули больше единицы. В отчёте о стабильности в статистических программах отражаются обычно величины, обратные к этим корням, поэтому условием стабильности будем считать наличие всех корней, по модулю меньших единицы.
Приведём пример оценённой VAR, используя временные ряды на рисунке
2.8. Закажем VAR(2), выбрав «Proc/Make Vector Autoregression…».
По умолчанию установим VAR(2) с константой в качестве экзогенной переменной. Щёлкнув «ОК», получим оценку VAR-модели (рисунок 3.1). Для каждого уравнения VAR-модели здесь рассчитываются традиционные показатели их точности. Как указано в заголовке окна отчёта, внизу под оценками параметров в круглых скобках указаны стандартные ошибки оценок, а ниже (в квадратных скобках) – соответствующие t-статистики. Считается, что если t-статистика меньше двух, то оценка незначимо отлична
65

от нуля. Если ориентироваться на это, то значимо отличаются от нуля в нашем примере в первом уравнении – оценки при переменных cprt-1, tbrt-1 и константы, а во втором уравнении – при переменной tbrt-1 и константы. Следовательно, можно было бы ограничиться оценкой модели VAR(1).
Рисунок 3.1 – Оценка VAR-модели
Оценённая VAR-модель имеет вид (с округлением во втором знаке и без учёта значимости оценок)
cprt = 0,66 + 0,5 cprt-1 – 0,22 cprt-2 + 0,72tbrt-1 – 0,02tbrt-2 + e1t, tprt = 0,47 -0,23 cprt-1 – 0,08 cprt-2 + 1,4tbrt-1 – 0,13tbrt-2 + e2t,.
Ниже (рисунок 3,2) приведена проверка VAR-модели на стабильность. Как видим, условие стабильности выполняется (все корни меньше единицы).
66

Рисунок 3.2 – Проверка VAR-модели на стабильность
3.2. Тест Гренджера на причинность
Приведём пример моделирования временных рядов, не удовлетворяющих условию стабильности VAR(2)-модели. Итак, пусть рассматриваются ряды, изображённые на рисунке 3.3. Здесь GDP – валовой национальный продукт, CS – совокупное потребление.
Рисунок 3.3 – Анализируемые ряды
Проведём тест на причинность по Гренджеру. Суть этого теста в следующем. Известно, что существование зависимости между переменными не означает причинную обусловленность. Установление причинноследственных связей не относится к области статистических исследований. Обычно это устанавливается на основе профессионально логических соображений. Но на основе статистических методов можно установить, улучшают ли прошлые значения одной переменной предсказания значений другой. Если это так, то говорят, что одна переменная является причиной (по Гренджеру) другой переменной.
67

Подобная причинность рассматривается в информационном аспекте, т.е. с определением того, что предшествует чему, а также с информативностью переменной с точки зрения прогнозирования другой переменной.
Причинность по Гренджеру применяется обычно к стационарным коинтегрированным временным рядам.
Тест Гренджера на причинность предполагает, что информация, относящаяся к предсказанию переменных, содержится исключительно во временных рядах этих переменных. Тест Гренджера включает оценку следующей пары регрессий
n |
|
n |
|
|
|
|
yt |
i xt i |
|
j yt |
j |
u1t , |
|
i 1 |
|
j |
1 |
|
|
|
n |
|
n |
|
|
|
|
xt |
i xt i |
|
j yt |
j |
u2t . |
|
i 1 |
|
j |
1 |
|
|
|
Здесь предполагается, что остатки регрессий не коррелированы. |
|
|||||
В контексте VAR переменная |
xt будет причиной yt , если коэффициенты |
|||||
при лагах xt в первом уравнении |
статистически значимы ( |
i 0 ), а |
||||
коэффициенты при лагах yt во втором уравнении статистически незначимы
( |
j |
0 ) и наоборот. Следует отметить, что возможна и двухсторонняя |
|
|
причинная связь: т.е. одновременно xt является причиной yt и yt является причиной xt (тогда обе группы обсуждаемых коэффициентов статистически значимы). А возможна и обоюдная независимость, когда обе группы коэффициентов статистически незначимы.
Для тестирования переменных на причинность по Гренджеру необходимо выполнить следующие действия (для первого уравнения).
1.Оценивается регрессия переменной yt на её лаговые значения, причём,
вэту регрессию не включаются лаговые значения другой переменной ( xt ), и
оценивается объяснённая сумма квадратов отклонений (RSS R ).
2.Оценивается регрессия с включением в неё лаговых значений обеих переменных, затем оценивается объяснённая сумма квадратов отклонений
(RSSUR ).
3. Нулевая гипотеза H 0 : |
i 0 , т.е. лаговые члены переменной xt не |
принадлежат этой регрессии.
4. Тестируется эта гипотеза на основе F-статистики:
68

F |
(RSSR |
RSSUR ) / m |
|
RSSUR |
/(n k) |
||
|
с числом степеней свободы числителя m, и знаменателя (n–k), где m – число лаговых переменных в уравнении регрессии, k – число параметров, оцениваемых в п. 2.
5.Если расчётное значение F-статистики больше критического, то нулевая гипотеза отклоняется и считается, что xt есть причина yt .
6.Шаги 1 – 6 могут быть повторены и для тестирования другого уравнения.
Следует отметить, что в этом тесте число лаговых членов в каждом уравнении может оказывать значимое влияние на конечное решение. Одна из рекомендаций в решении этой проблемы предлагает использование информационных критериев Акаике и Шварца. Кроме того, значимые выводы здесь можно получить только лишь на основе F-статистик, но не на основе тестирования отдельно коэффициентов моделей.
На рисунке 3.4 приведён тест Гренджера на причинность ранее рассматриваемых двух переменных. Вывод на основе этого теста такой: если выбрать число лагов, равное 6, то гипотеза о независимости GDP от CS (на 5%-ном уровне значимости) отклоняется (Probability = 0,00012), противоположная гипотеза, что GDP не есть причина CS, не отклоняется (Probability = 0,59528). Т.е. в нашем примере установлена следующая причинность по Гренджеру : CS есть причина GDP, а обратное неверно.
Рисунок 3.4 – Тест Гренджера на причинность
69

3.3. Модель коррекции остатков для нестационарных временных рядов
Как уже обсуждалось, при моделировании зависимости временных рядов на основании уравнения регрессии близость к единице наблюдаемого коэффициента детерминации не обязательно означает наличие причинной связи между ними, а может являться лишь следствием наличия тренда в уровнях обоих рядов.
При этом ложная регрессия (паразитная связь) может возникнуть между временными рядами как с детерминированными, так и со стохастическими трендами. В последнем случае, как правило, вместе с относительно высоким значением коэффициента детерминации наблюдается также крайне низкое значение статистики Дарбина – Уотсона.
Вопрос о ложной или не ложной линейной регрессионной связи между двумя I(1) временными рядами сводится к выяснению, являются ли эти ряды коинтегрированными. Два I(1) временных ряда xt и yt называются коинтегрированными, если существует ненулевой (коинтегрирующий)
вектор |
( |
1 |
, |
2 |
)Т , для которого линейная комбинация |
1 |
x |
t |
2 |
y |
t |
является |
|
|
|
|
|
|
|
||||||
стационарным |
|
I(0)-рядом. Известно, что коинтегрирующий |
вектор |
|||||||||
определяется с точностью до постоянного множителя, поэтому для выделения определённого вектора вводят условие нормировки, например,
рассматривается |
вектор (1, |
)Т . |
Если |
такой вектор существует, то это |
значит, что линейная комбинация |
yt |
xt является стационарным I(0)-рядом. |
||
В этом случае |
уравнение |
yt |
xt |
определяет уравнение равновесия |
рассматриваемых рядов в долгосрочной перспективе, а абсолютная величина zt yt 
 xt может рассматриваться как расстояние, отделяющее систему в момент t от равновесия. Ряд zt является стационарным рядом с нулевым математическим ожиданием.
xt может рассматриваться как расстояние, отделяющее систему в момент t от равновесия. Ряд zt является стационарным рядом с нулевым математическим ожиданием.
Если система коинтегрированных рядов xt и yt допускает AR(p)
представление, то её можно представить в виде следующей модели коррекции остатков, или ошибок (error correction model – ECM):
|
|
p |
1 |
|
|
xt |
1 |
1 zt 1 |
( 1 j xt j |
1 j yt j ) |
1 j , |
|
|
j |
1 |
|
(3.1) |
|
|
|
|
70
