I. Задачи элементарной математики

§ 1. Линейная функция. Уравнение прямой. Парабола

Линейная функция называется также линейной зависимостью или линейной регрессией. Уравнение подчёркивает, что y зависит от x, а не наоборот. Уравнение , напротив, указывает на равноправие переменных и применяется, когда линейная комбинация образует новую величину, например, производственные затраты.

Любая линия (не только прямая) пересекает ось абсцисс (ось OX), когда , а ось ординат (ось OY) – если . Поэтому для поиска точек пересечения линии с системой координат подставляем эти значения по очереди в уравнение линии, находим другую координату и тем самым – точку пересечения.

С точки зрения математического анализа запись точнее. Принятая форма записи связана с традициями аналитической геометрии.

ЛФ1. Отметьте точки в декартовой системе координат:

1)

2)

3)

4)

ЛФ2. Постройте прямые, параллельные осям координат:

1) а) ; б) ; в) ; г) ; д) ; е) ;

2) а) ; б) ; в) ; г) ; д) ; е) .

Как выглядят прямые и ?

ЛФ3. Постройте прямые, определив точки пересечения с осями координат:

1) а) ; б) ; в) ; г) ;

2) а) ; б) ; в) ; г) ;

3) а) ; б) ; в) ; г) ;

4) а) ; б) ; в) ; г) ;

5) а) ; б) ; в) ; г) ;

6) а) ; б) ; в) ; г) .

Пример 1. Построим прямую .

Если , то , откуда и соответственно . Значит, прямая пересекает ось OY (на которой ) в точке .

Если же , то , откуда . Поэтому прямая пересекает ось OX (на которой ) в точке .

Отмечаем на оси OX точку , на оси OY точку и проводим прямую, проходящую через эти точки.

Пример 2. Построим прямую :

а) если , то , откуда и ;

б) если , то , откуда и .

Отмечаем на оси OX точку , на оси OY точку , и проводим прямую, проходящую через точки.

ЛФ4. Постройте прямые, заданные уравнением с угловым коэффициентом:

1) а) ; б) ; в) ; г) ; д) ;

2) а) ; б) ; в) ; г) ; д) ;

3) а) ; б) ; в) ; г) ; д) ;

4) а) ; б) ; в) ; г) ; д) .

Пример 3. Построим прямую :

а) пусть , тогда . Отмечаем точку ;

б) пусть , тогда . Отмечаем точку .

Прямая проходит через А и В (и продолжается в обе стороны).

Замечание. При слишком близких значениях x прямая получится неточно. Не следует также брать x, при которых получается большое (по модулю) значение y.

ЛФ5. Постройте прямые, обращая внимание на зависимость расположения прямой от знака и величины коэффициентов:

1) а) ; б) ; в) ; г) ;

д) ; e) ; ж) ; з) ;

2) а) ; б) ; в) ; г) ;

д) ; e) ; ж) ; з) ;

3) а) ; б) ; в) ; г) ;

д) ; e) ; ж) ; з) ;

4) а) ; б) ; в) ; г) ;

д) ; e) ; ж) ; з) .

ЛФ6. Постройте параболы любым способом:

1) а) ; б) ; в) ; г) ;

д) ; e) ; ж) ; з) ;

2) а) ; б) ; в) ; г) ;

д) ; e) ; ж) ; з) ;

3) а) ; б) ; в) ; г) ;

д) ; e) ; ж) ; з) ;

4) а) ; б) ; в) ; г) ;

д) ; e) ; ж) ; з) .

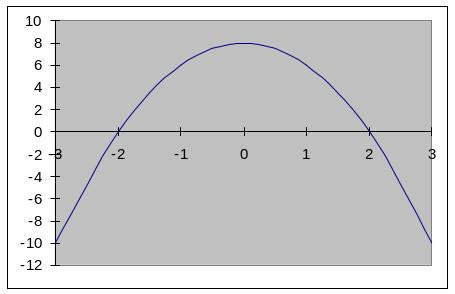
Пример 4. Построим параболу .

Если , то . Парабола пересекает ось OY в точке .

Чтобы найти точки пересечения с осью OX, решаем уравнение , получаем точки и .

Перед квадратом стоит знак «–». Значит, ветви направлены вниз. В уравнении отсутствует линейное слагаемое px, поэтому вершина находится на оси OY. Общий вид параболы дан на рисунке 1. Ось OY проходит через точку .

Рисунок 1 – Парабола

ЛФ7. Постройте параболы, указав вершину и точки пересечения с осями координат (если такие точки есть):

1) а) ; б) ; в) ;

г) д) ; е) ;

2) а) ; б) ; в) ;

г) д) ; е) ;

3) а) ; б) ; в) ;

г) д) ; е) ;

4) а) ; б) ; в) ;

г) д) ; е) .

Пример 5. Построим параболу .

Пусть , тогда . Парабола пересекает ось OY в точке .

Решим уравнение . Получим точки и . В них парабола пересекает ось OX.

Когда парабола задана уравнением , её вершина находится по формуле . В нашем случае , поэтому . Соответственно, , и вершина – в точке . Ветви идут вверх – перед квадратом в уравнении стоит знак «+». Ось OY проходит через (рисунок 2).

Рисунок 2 – Парабола

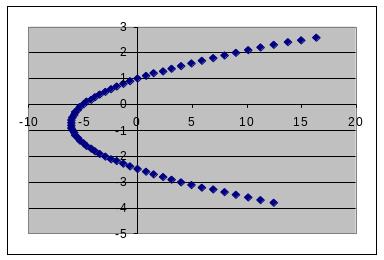
Пример 6. Построим параболу .

Ветви направлены по горизонтали, поскольку x квадратично зависит от y. При этом перед квадратом в уравнении стоит знак «+» и ветви идут в положительном направлении – вправо.

Пусть , тогда . Решение уравнения – точки и , в них парабола пересекает ось OY.

Если , то и парабола пересекает ось OX в .

Вершину находим по формуле при , поэтому . При этом . Вершина параболы находится в точке (рисунок 3).

Рисунок 3 – Парабола