
492_Nosov_V._I.__Metody_povyshenija_pomekhoustojchivosti_sistem_radiosvjazi_..
._.pdf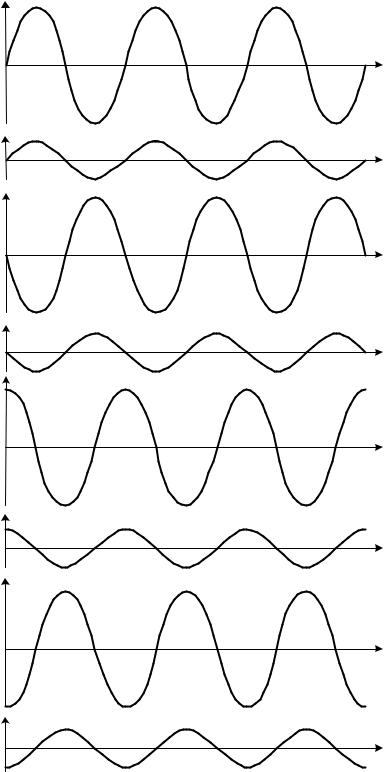
f3 t |
|
|
а |
|
t |
f3 t |
б |
|
t |
f3 t |
|
|
в |
|
t |
f3 t |
г |
|
t |
f3 t |
|
|
д |
|
t |
f3 t |
е |
|
t |
f3 t |
|
|
ж |
|
t |
f3 t |
з |
|
t |
Рис. 3.12. Формирование сигнала поднесущей для 16-QAM |
|
141

При такой комбинации потоков d4d3 01 из |
устройства формирования |
||
считывается отрезок поднесущей с амплитудой 3L |
|
|
и фазой 00, эпюра а) |
|
10 |
||
на рис. 3.12. |
|
|
|
При формировании первой сигнальной точки на выходе устройства размещения в квадратурном канале Q формируется комбинация двух потоков d2d1 01,
что соответствует уровню сигнала 3L. При такой комбинации потоков d2d1 01 из устройства формирования считывается отрезок поднесущей с амплитудой 3L

 10 и фазой 900, эпюра д) на рис. 3.12.
10 и фазой 900, эпюра д) на рис. 3.12.
В соответствии с рис. 3.7, при формировании девятой сигнальной точки на вход устройства размещения поступает комбинация четырёх цифровых потоков d4d3d2d1 1001. При этом, на выходе устройства размещения в синфазном канале
I формируется комбинация двух потоков d4d3 10 , что соответствует уровню сигнала 1L. При такой комбинации потоков d4d3 10 из устройства формирова-
ния считывается отрезок поднесущей с амплитудой L

 10 и фазой 1800, эпюра г)
10 и фазой 1800, эпюра г)
на рис. 3.12.
При формировании девятой сигнальной точки на выходе устройства размещения в квадратурном канале Q формируется комбинация двух потоков d2d1 01,
что соответствует уровню сигнала 3L. При такой комбинации потоков d2d1 01 из устройства формирования считывается отрезок поднесущей с амплитудой 3L

 10 и фазой 900, эпюра д) на рис. 3.12.
10 и фазой 900, эпюра д) на рис. 3.12.
Аналогичным образом формируются сигналы в синфазном и квадратурном каналах для других сигнальных точек и других позиционностей модуляции.
Сформированные в синфазном и квадратурном каналах отрезки сигналов поднесущих частот на выходе блока модулятора в соответствии с (3.13) и (3.14) можно представить в виде
sk t skI t akI sin 2 f0 k f t kI akQ sin 2 f0 k f t kQ . (3.19)
Поскольку амплитуда модулированного сигнала akI и akQ на интервале
символа модуляции, определяется для каждой сигнальной точки из диаграммы Грея (рис. 3.7 ÷ 3.9) и принимает положительные и отрицательные значения, значения фазы kI и kQ в выражении (3.16) можно опустить.
142

Суммарный сигнал на выходе блока модуляторов (рис. 3.6) на всех поднесущих частотах можно записать
N |
k f t, |
|
s t Ckej2 f0 |
(5.20) |
k 0
где f0 = 0; N – количество поднесущих частот; Ck – комплексная амплиту-
да k-ой поднесущей, действительная akI и мнимая akQ составляющие соответ-
ствуют синфазному I и квадратурному Q каналам квадратурной амплитудной модуляции. Значения этих амплитуд выбираются в соответствии с диаграммами Грея (рис. 3.7 ÷ 3.9), исходя из значения модуляционного символа.
Сигналы с выхода блока модулятора подаются на вход блока обратного быстрого преобразования Фурье ОБПФ (IFFT – Inverse Fast Fourier Transformation).
Далее рассмотрим особенности обработки сигнала при проведении преобразования Фурье.
3.5 Преобразование Фурье
3.5.1 Дискретизация сигнала во времени, спектр дискретного сигнала
Пара непрерывного преобразования Фурье (интеграл Фурье) имеет вид:
S s t exp j t dt;
(3.21)
1
s t 2 S exp j t d ,
где S – спектр сигнала s t (в общем случае и сигнал и спектр – ком-
плексные).
143

Выражения для прямого (ДПФ) и обратного дискретного преобразования Фурье (ОДПФ) имеют вид:
|
N 1 |
|
2 |
|
|
|
|
|||
S k s n exp j |
n k , |
k 0,1,...,N 1; |
||||||||
|
||||||||||
|
n 0 |
|
N |
|
|
(3.22) |
||||
|
1 |
N 1 |
|
|
2 |
|
|
|||
|
|
|
|
|||||||
s n |
|
S k exp |
j |
|
|
n k |
, |
n 0,1,...,N 1. |
||
|
N |
|||||||||
|
N k 0 |
|
|
|
|
|
||||
Выражение для ДПФ (3.22) ставит в соответствие N отсчетам сигнала, s(n), в общем случае комплексного, N отсчетов спектра S(k).
Можно обратить внимание, что как и в непрерывном, так и в дискретном случае, в выражении для обратного преобразования имеется нормировочный
коэффициент. В случае интеграла Фурье это, 12 в случае ОДПФ – 1N . Можно отметить, что в случае непрерывного преобразования нормировочный коэффици-
ент 12 1dt d призван корректно отображать масштабирование сигнала
во времени в частотную область и наоборот. Другими словами, если последовательно рассчитать спектр некоторого сигнала, а после взять обратное преобразование Фурье, то результат обратного преобразования должен полностью совпадать с исходным сигналом. Нормировочный коэффициент уменьшает амплитуду сигнала на выходе обратного преобразования для того чтобы она совпадала с амплитудой исходного сигнала.
Рассмотрим теперь сигнал sd t как результат умножения непрерывного сигнала на решетчатую функцию,
N 1 |
N 1 |
|
sd t s t t n t |
s t t n t , |
(3.23) |
n 0 |
n 0 |
|
где t – дельта-функция; |
|
|
, |
t 0, |
|
t |
t 0. |
(3.24) |
0, |
|
|
|
|
|
t – интервал дискретизации.
144

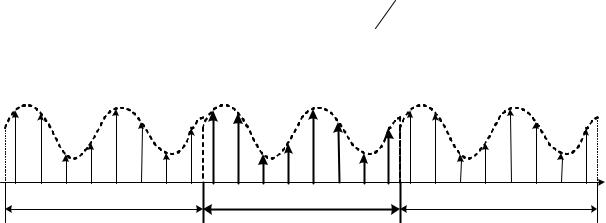
Графически процесс дискретизации можно представить, как это показано на рис. 3.13.
Вычислим спектр дискретного сигнала sd t , для этого подставим выраже-
ния для дискретного сигнала (3.22) в выражения для преобразования Фурье (3.20), и получим:
|
N 1 |
S sd t exp j t dt s t t n t exp j t dt. (3.25)
|
n 0 |
s t
t
|
|
|
|
|
|
|
|
t
0 |
1 |
2 |
3 |
4 |
t |
N 1 |
sd t
t
0 |
1 |
2 |
3 |
4 |
N 1 |
Рис. 3.13. Процесс дискретизации сигнала
145

Поменяем местами операции суммирования и интегрирования и применим фильтрующее свойство дельта-функции:
|
x t |
|
t |
|
dt |
|
x |
. |
|
|
|
|
|
(3.26) |
|||||
|
|
|
|
|
|
Тогда выражение (3.25) с учетом (3.26):
N 1 |
|
n 1 |
S s t t n t exp j t dt s n t exp j n t . (3.27)
n 0 |
n 0 |
Таким образом, мы избавились от интегрирования в бесконечных пределах, заменив конечным суммированием комплексных экспонент. Но пока частота меняется на всей числовой оси. Однако можно заметить, что комплексные экспоненты под знаком суммы в выражении (3.27) являются периодическими функциями с периодом:
n |
2 |
, |
n 1,2,...,N 1. |
(3.28) |
|
||||
|
n t |
|
|
|
Необходимо отметить, что n = 0 исключено из выражения (3.28), так как при n = 0 комплексная экспонента равна единице для всех частот. Таким образом, максимальный период повторения спектра S будет при n = 1 и равен
2
max 1 t . (3.29)
В результате можно рассматривать только один период повторения спектра
S при 0... max .
3.5.2 Повторение сигнала во времени. Дискретное преобразование Фурье
Для цифровой обработки требуются как дискретные отсчеты сигнала, так и дискретные отсчеты спектра. Известно, что дискретный (или как еще говорят линейчатый спектр) имеют периодические сигналы, а линейчатый спектр получается путем разложения в ряд Фурье периодического сигнала. Значит, чтобы полу-
146
чить дискретный спектр, надо сделать исходный дискретный сигнал периодическим, или другими словами необходимо повторить данный сигнал во времени бесконечное количество раз с некоторым периодом , тогда его спектр будет
содержать дискретные гармоники кратные 2 T . Графически процесс повто-
рения сигнала во времени представлен на рис. 3.14.
t
0 |
N 1 0 |
N 1 0 |
N 1 |
T |
T |
|
T |
Рис. 3.14. Повторение сигнала во времени
Жирными линиями показан исходный сигнал, тонкими – его повторения через некоторый период .
Как следует из рис. 3.14, повторять сигнал можно с различным периодом Т, однако, необходимо чтобы период повторения был более или равен длительности сигнала, т.е. T N t. При этом минимальный период повторения сигнала
Tmin N t. |
(3.30) |
Это тот минимальный период, при котором сигнал и его повторения не накладываются друг на друга. Повторение сигнала с минимальным периодом Tmin N t представлен на рис. 3.14.
При повторении сигнала с минимальным периодом получим линейчатый спектр сигнала, состоящий из гармоник кратных
|
2 |
|
2 |
, |
(3.31) |
Tmin |
|
||||
|
|
N t |
|
||
и на одном периоде 0... max получим
147

2
max |
|
|
t |
|
|
N |
(3.32) |
|
|
|
2 |
|
|
||||
|
|
|
|
|
|
|||
N t
гармоник спектра.
Таким образом, мы можем продискретизировать спектр дискретного сигнала на одном периоде повторения 0... max с шагом 2 N t и получим тем самым N отсчетов спектра. Учтем вышесказанное в выражении (3.27), получим:
N 1
S k s n t exp j n t k
|
n 0 |
|
|
|
|
|
|
|
|
|
N 1 |
|
|
|
|
|
2 |
|
|
||
|
|
|
|
|
|
|
||||
s n t exp |
j |
n t k |
|
|
|
|
(3.33) |
|||
N |
|
|||||||||
n 0 |
|
|
|
|
|
t |
|
|
||
N 1 |
|
|
2 |
|
|
|
|
|
|
|
s n t exp j |
|
n k , |
|
k 0,1,...,N 1. |
|
|||||
|
|
|
|
|||||||
n 0 |
|
|
N |
|
|
|
|
|
|
|
Если опустить в выражении (3.33) шаг дискретизации по времени t и по частоте , то получим окончательное выражение для ДПФ:
N 1 |
|
2 |
|
|
|
|
S k s n exp j |
n k , |
k 0,1,...,N 1. |
(3.34) |
|||
N |
||||||
n 0 |
|
|
|
|
||
Можно сделать вывод, что ДПФ ставит в соответствие N отсчетам дискретного сигнала N отсчетов дискретного спектра, при этом предполагается, что и сигнал и спектр являются периодическими и анализируются на одном периоде.
3.5.3 Обратное дискретное преобразование Фурье
Аналогично (3.22) можно записать выражение для дискретного спектра через решетчатую функцию
N 1 |
|
Sd S k , |
(3.35) |
k 0
148

где Sd – дискретные отсчеты спектра на одном периоде повторения
0... max .
Подставим значение Sd (3.35) в выражение для обратного преобразования Фурье (3.20):
|
N 1 |
s t C Sd exp j t d C S k exp j t d , (3.36)
|
k 0 |
где C 1N – коэффициент пропорциональности, задача которого обеспе-
чить равенство по амплитуде исходного дискретного сигнала и результата ОДПФ.
Коэффициент пропорциональности учитывает коэффициент 12 . Поменяв ме-
стами операции суммирования и интегрирования с учётом фильтрующего свойства дельта-функции, получим
|
|
1 |
N 1 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
N 1 |
|
|
|
|
|
|
(3.37) |
|||||
s t |
N |
|
S |
|
|
k |
|
|
N |
|
S k |
|
exp jk |
||||||||||||||||
|
|
|
|
|
|
|
|
exp j t d |
|
|
|
|
|
t . |
|
||||||||||||||
|
|
|
k 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k 0 |
|
|
|
|
|
|
|
|
Возьмем дискретные отсчеты s t |
через интервал t , |
тогда (3.37) |
можно |
||||||||||||||||||||||||||
записать |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
N 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
s n t |
|
S k exp jk n t , |
n 0,1,...,N 1. |
(3.38) |
||||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
N k 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Учтем (3.31) и получим: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
1 |
|
N 1 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
s n t |
|
|
S k exp j |
k n , |
n 0,1,...,N 1. |
(3.39) |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
N k 0 |
|
|
|
|
N |
|
|
|
|
|
|
|
|
|||||||
Опустив в выражении (3.39) интервалы дискретизации по частоте и по времени, оставив только индексы получим выражение для ОДПФ
|
1 |
N 1 |
|
2 |
|
|
|
|
s n |
S k exp j |
k n , |
n 0,1,...,N 1. |
(3.40) |
||||
|
N |
|||||||
|
N k 0 |
|
|
|
|
|||
|
|
|
149 |
|
|
|
|
|

3.5.4 Индексация спектральных отсчетов. Перестановка спектральных отсчетов
Таким образом, в подразделе 3.5.3 получены выражения как для прямого ДПФ, так и для обратного ОДПФ. По материалу этого подраздела можно сделать несколько выводов.
Вывод 1. Расчет ДПФ и ОДПФ ведется на основе индексов временных n 0,1,...,N 1 и спектральных k 0,1,...,N 1 отсчетов без учета частоты дискретизации. Это позволяет использовать выражения для ДПФ и ОДПФ при любой частоте дискретизации не меняя вычислительную программу. Это несомненный плюс ДПФ. При этом если необходимо привязать индексы к частоте дискретизации (к реальной оси частот), то нужно вспомнить, что частотный спектр дискретизиро-
вался с шагом f |
1 |
Гц, или 2 |
рад/c, где t |
1 |
, F f – |
|
N t |
N t |
|
F |
d |
|
|
|
|
d |
|
частота дискретизации в Гц. Таким образом, если известна частота дискретизации Fd (разнос соседних поднесущих f ), то k-ый спектральный отсчёт соответствует частоте k рад/c или f k f Гц.
Например, при ширине полосы частот, занимаемой системой радиосвязи
BW 10 МГц и N 32, частота дискретизации Fd |
или разнос соседних поднесу- |
||||||
щих f , равны |
|
|
|
|
|
|
|
F f |
BW |
|
10000 кГц |
312,5 кГц. |
(3.41) |
||
|
|
||||||
d |
|
N |
32 |
|
|
|
|
|
|
|
|
|
|||
При этом, спектральный |
отсчет при |
k 17 соответствует |
частоте |
||||
f 312,5 17 5312,5 кГц. |
|
|
|
|
|
|
|
Вывод 2. Дискретизация спектра при ДПФ осуществлялась на одном перио- |
|||||||
де повторения спектра 0... max . |
При этом в силу периодичности спектра |
||||||
дискретного сигнала отсчеты S k |
|
при k N 2,...,N соответствуют как частотам |
|||||
k k , так и частотам k k max , где max N , то есть S k
при |
k N 2,...,N |
соответствуют |
отрицательным |
частотам |
|
k k N k N , т.е. физически при k N |
,...,N вторая поло- |
||||
|
|
|
2 |
|
|
вина спектра это частоты от max 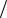 2 ,...,0 . Это наглядно иллюстрируется рис. 3.15. Для того, чтобы из спектра в интервале частот 0... max , рассчи-
2 ,...,0 . Это наглядно иллюстрируется рис. 3.15. Для того, чтобы из спектра в интервале частот 0... max , рассчи-
танного при помощи дискретного преобразования Фурье, получить спектр сигнала
150
