
409_Arhipov_Chuhrov-diskr_soobsch_Monografiya
.pdf
ми и состоятельными, т.е. даже при увеличении времени наблюдения Т, дисперсия оценки СПМ не стремится к нулю. Известно, что, если имеется состоятельная оценка некоторой статистической характеристики (например, оценка корреляционной функции - состоятельная оценка), то ее преобразование Фурье не является состоятельной оценкой.
Поэтому периодограммы нельзя считать оценками СПМ. В качестве оценки СПМ необходимо принять математическое ожидание периодограммы, или, на практике - его выборочную характеристику - арифметическое среднее. Практически это означает, что периодограммы или выборочные спектры необходимо усреднять по большому числу реализаций.
Совместное использование окон и усреднения имеет особенности, связанные с коррелированностью соседних периодограмм. Для уменьшения корреляции используют либо специальные виды окон, либо так разбивают отдельные реализации, чтобы корреляция перекрывающихся участков была минимальна. В любом случае неизбежна некоторая потеря информации.
4. Метод БПФ обладает «эффектом частокола», который связан с тем, что при попадании какой-либо спектральной линии на середину между отсчетами БПФ, оценка этой спектральной линии уменьшается (в предельном случае в /2 1,57 раз). Для уменьшения этого эффекта используется дополнение последовательности x(k) нулями, что также увеличивает время вычислений.
Как известно, функция Sin x имеет значительные боковые лепестки, x
которые медленно уменьшаются с ростом m . Это приводит к просачиванию энергии в соседние и далеко отстоящие спектральные отсчеты, то есть к маскированию слабых спектральных линий. Для уменьшения этих вредных явлений в качестве окон w(k) используются функции, имеющие в центре интервала (0, T) максимум и медленно спадающие до 0 к краям интервала, то есть симметричные относительно середины интервала (0, T).
Чаще для выбора того или иного окна w(k), предъявляют требования к его преобразованию Фурье, то есть к спектральному окну W m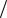 N . В частности, основными требованиями к W m f являются следующие:
N . В частности, основными требованиями к W m f являются следующие:
спектральное окно должно иметь возможно более узкий центральный пик;
число боковых выбросов должно быть небольшим, а их амплитуда малой, то есть скорость спада боковых лепестков – большая;
отрицательные выбросы, если возможно, должны отсутствовать;
формула для вычисления окна должна быть по возможности простой. Перечисленные требования во многом противоречивы. В настоящее
время синтезировано множество различных окон, удовлетворяющих тому или иному критерию или комплексу критериев. В любом случае выбор оптимального окна определяется априорной информацией о сигнале, о помехах, а также требованием к точности обработки и скорости вычислений. Для линейчатых спектров (какими можно считать спектры узкополосных помех) наиболее
11

приемлемыми являются окна:
|
|
m |
|
|
|
|
2 |
|
|
|
|
||||
– Хэмминга: |
w |
|
|
|
|
0,54 0,46 cos |
|
|
( m 1) , |
|
|
|
|||
|
|
N |
|
|
|
||||||||||
|
|
N |
|
|
|
|
|
|
|
|
|||||
|
m |
|
2 |
|
|
4 |
|
|
|||||||
– Блекмана: |
w |
|
|
|
0,42 0,5cos |
|
m 1 |
0,08cos |
|
|
m 1 |
, |
|||
|
|
|
|
N |
|||||||||||
|
N |
|
N |
|
|
|
|
|
|||||||
(1.1)
(1.2)
имеющие, соответственно следующие характеристики:
|
ширина основного лепестка на уровне 3 - 1,3 дБ и 1,68 дБ соответственно; |
|
уровень первого бокового лепестка - 43 дБ и - 58 дБ соответственно. |
Для сравнения ширина основного лепестка для прямоугольного окна равна 0,88 (в относительных единицах), а уровень первого бокового лепестка - 13 дБ.
1.2.2 Оценивание УП на основе AРСС аппроксимации
При использовании авторегрессионной модели УП оценку спектральную плотность мощности АР-процесса можно получить в виде [127]
S( f ) |
2 |
t |
|
|
|
|
, |
(1.3) |
|
P |
2 |
|||
|
|
|
|
|
1 ak exp( j2 fk t )
k 1
где 2 – дисперсия шума, Р – порядок АР-модели.
Таким образом, для получения оценки СПМ необходимо оценить значе-
ния параметров АР-модели a1 ,a2 ,..., a p , 2 . Если корреляционная функ-
ция (КФ) Rxx(k) анализируемой последовательности х(n) известна или оценена, то значения параметров АР-модели и КФ связаны системой линейных уравнений
|
|
|
|
|
|
P |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
akRxx(k l ), |
k 0 |
|
|
|
|
|
|||||
|
|
|
|
|
|
l 1 |
|
|
|
|
|
|
|
|
|
|
|
|
Rxx( k ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
P |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
k 0, |
|
|
|
||||
|
|
|
alRxx(k l ) 2, |
|
|
|
|
||||||||||
|
|
|
|
l 1 |
|
|
|
|
|
|
|
|
|
|
|
||
или в матричной форме: |
|
|
|
|
|
|
|
|
|
|
|||||||
|
R |
(0) |
R |
|
( 1) ... |
R ( P) |
|
|
1 |
|
|
2 |
|
|
|||
|
|
|
|
|
|
||||||||||||
|
xx |
|
xx |
|
|
|
xx |
|
|
a |
|
|
|
|
|||
|
R |
(1) |
R |
|
|
(0) ... |
R ( P 1) |
* |
|
0 |
|
. |
|||||
|
xx |
xx |
|
... |
xx |
|
|
1 |
|
||||||||
|
... |
|
... |
... |
|
|
... |
|
... |
|
|
||||||
|
R (P) |
R |
(P 1) ... |
R (0) |
|
|
a |
p |
|
0 |
|
|
|||||
|
xx |
|
xx |
|
|
|
|
xx |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1.4)
(1.5)
Эти уравнения называют уравнениями Юла-Уокера.
Для определения АР-параметров модели необходимо выбрать из (1.4)
12
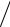
Р – уравнений при k > 0, решить их относительно {a1, a2, … ap} и затем определить 2 при k = 0.
Решение уравнений (1.4) возможно различными методами. В частности, к данным уравнениям применим метод гауссова исключения, однако, приблизительное число операций равно Р3, что при значительных величинах Р неприемлемо.
Для спектрального оценивания значения КФ могут быть применены следующие известные алгоритмы:
алгоритм Левинсона;
алгоритм Берга;
алгоритм Писаренко (оценивание на основе аппроксимации набором синусоид);
алгоритм Прони (оценивание на основе аппроксимации набором затухающих экспонент);
адаптивные алгоритмы вычисления АР-параметров (решетчатые фильтры).
Поскольку матрица Rxx(k) – симметричная, существует эффективный алгоритм решения системы уравнений (1.5), разработанный Левинсоном, Дербином и другими [128]. В дальнейшем для краткости метод решения уравнений Юла-Уокера будет именоваться алгоритмом Левинсона. Этот алгоритм позволяет рекурсивно вычислять набор параметров:
a11, 12 , a21,a22 , 22 ,..., ap1 ,ap2 ,...,app , 2p ,
где дополнительный индекс введен для обозначения порядка АР-процесса. Алгоритм Левинсона инициализируется коэффициентами:
a |
11 |
R |
xx |
1 / R |
xx |
0 |
|
|||||||
|
|
|
|
|
|
|
|
|
, |
|||||
|
|
2 |
|
|
1 |
|
a |
|
2 |
|
|
0 |
|
|
|
|
|
|
|
||||||||||
1 |
|
|
11 |
R |
xx |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
а рекурсии для К=2, 3, ..., p вычисляются с помощью выражений:
|
|
|
|
k 1 |
|
k2 1 |
|
akk Rxx( k ) ak 1,lRxx k l |
, |
||||||
|
|
|
|
l 1 |
|
|
|
|
|
|
|
|
|
|
|
aki ak 1,i akkak 1,k i , |
|
|
|
||||
|
|
. |
|||||
2 |
|
|
|
2 |
|
|
|
1 |
akk |
|
|
|
|||
k |
|
k 1. |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
(1.6)
(1.7)
Этот алгоритм имеет следующие преимущества по сравнению с другими методами решения системы (1.4):
13
поскольку параметры вычисляются по рекуррентным формулам, то до определения параметров АР-модели порядка Р рассчитываются параметры АР-моделей более низких порядков; это – весьма полезное свойство в тех случаях, когда значение Р заранее неизвестно;
в ходе вычислений легко контролировать необходимое и достаточное
условие устойчивости АР-модели: |
a ll |
1 , |
l 1 ,2 , ..., P ; |
для параметров АР-модели порядка Р требуется выполнить всего около Р2 арифметических операций.
Часто при спектральном оценивании значения КФ Rxx(k) неизвестны. В
этом случае определение параметров АР-модели необходимо выполнять, располагая только отсчетами Х(п) анализируемого процесса. Наиболее известным подходом оценивания АР-параметров по отсчетам данных является алгоритм Берга, который можно рассматривать как минимизацию методом наименьших квадратов [64]:
p |
|
N |
|
|
l pn |
|
2 |
|
|
bpn |
|
2 |
, |
(1.8) |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|||||||
|
|
n p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
при ограничении, что параметры АР-модели должны удовлетворять рекурсивному уравнению Левинсона
a pn a p 1,k a pp a p 1,p k . |
|
|
|
|
|
|
|
|||||||||
В (1.8) |
величины lpп |
|
и bрп представляют собой ошибки линейного |
|||||||||||||
предсказания вперед и назад, соответственно |
|
|
|
|||||||||||||
|
|
|
|
P |
|
|
|
|
P |
|
|
|
|
|
|
|
lpn Xn Xˆn Xn apkXn k apkXn k |
|
|
|
|||||||||||||
|
|
|
|
k 1 |
|
|
|
|
k 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P |
|
. |
(1.9) |
|||
|
ˆ |
|
|
|
|
|
P |
|
|
|
||||||
|
|
Xn p |
|
|
|
|
|
|
|
|
|
|
|
|
||
bpn Xn p Xn p |
apkXn p k |
apkXn p k |
|
|
||||||||||||
|
|
|
|
|
|
|
k 1 |
|
|
k 0 |
|
|
|
|||
Приравняв к нулю производную р |
по аii , |
получаем выражение для |
||||||||||||||
расчета параметров: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
N 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 bi 1,k 1li 1,k |
|
|
|
|
|
|
|
||||||||
aii |
|
|
|
k i |
|
|
|
|
|
|
|
|
. |
|
|
(1.10) |
N 1 |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
li 1,k |
|
2 |
|
|
bi 1,k 1 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
k i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Недостатком алгоритма Берга является расщепление спектральных линий и смещение спектральных оценок по частоте, особенно при больших отношениях сигнал/шум и коротких временных последовательностях данных.
14
Эти недостатки можно значительно сгладить проведя минимизацию ошибки предсказания р по всем АР-параметрам от ар1 до арр. При этом требуется примерно на 20% больше вычислений, однако улучшение результатов значительно перевешивают затраты на дополнительные вычисления:
меньшее частотное смещение оценок спектральных составляющих;
уменьшение дисперсии частотных оценок;
отсутствие эффекта расщепления спектральных линий.
Если случайный процесс (совокупность УП) состоит из смеси синусоид
иаддитивного белого шума, то его можно моделировать как частный случай АРСС-процесса, у которого порядок АР и СС-процессов равны. Этот АРССпроцесс обладает частным видом симметрии, в результате чего АРпараметры оказываются идентичными СС-параметрам модели.
Наблюдаемый процесс Yп, состоящий из смеси p синусоид и шума, имеет вид:
2P |
|
Yn Xn n amXn m n. |
(1.11) |
m 1 |
|
Если КФ процесса Yn известна, то АРСС-параметры можно найти из |
|
уравнения |
|
RyyA w2A, |
(1.12) |
где
R (0) |
|
|
yy |
Ryy |
|
R (2P) |
|
|
yy |
Ryy( 2P)
– корреляционная матрица процесса Yn;
Ryy(0)
АТ = [1, а1, …, а2Р] – вектор АРСС-параметров.
Уравнение (1.12) представляет собой уравнение процесса, в котором дисперсия шума w2 является собственным значением корреляционной матрицы Ryy, а вектор АРСС-параметров А является собственным вектором, свя-
занным с собственным значением w2 и пронормированным так, чтобы первый элемент был равен 1.
Если число синусоид в смеси неизвестно, то уравнение (1.12) необходимо решать для последовательно возрастающих порядков p до тех пор, пока минимальное собственное значение перестанет изменяться при переходе к следующему более высокому порядку. Этот алгоритм носит название алго-
ритма Писаренко.
Недостатки алгоритма Писаренко:
алгоритм плохо работает при высоком уровне шума;
определение корней уравнения (1.12) требует больших вычислительных затрат.
15

Модель, используемая в алгоритме Прони, представляет собой набор из Р экспоненциальных функций с произвольными амплитудами, частотами, фазами и затуханиями:
Xˆ n |
P |
|
bm Zmn 1, |
(1.13) |
m 1
где для общности величины bm и Zm полагаются комплексными:
bm Am exp( j m ),
Zm exp[( m j2 fm ) t].
Отыскание параметров { Am,αm, fm, m }, минимизирующих среднеквадратичную ошибку
N
xn xˆn 2 ,
n 0
представляет собой нелинейную задачу аппроксимации по методу наименьших квадратов. Аналитические методы решения этого уравнения отсутствуют. Для минимизации ошибки по всем экспоненциальным параметрам используются итеративные алгоритмы (градиентного спуска, Ньютона), посредством которого первоначально принятые оценки значений этих параметров постепенно улучшаются. Если предположить, что аппроксимирующая функция имеет форму:
P |
|
Xˆ (t) Am exp( m t )exp[ j(2 fmt m )], |
(1.14) |
m 1
то для вещественного процесса Х(t) потребуются комплексно-сопряженные пары типа:
exp j 2 fmt m и exp j 2 fmt m .
Далее предполагается, что коэффициенты затухания отрицательны, поэтому получаются затухающие экспоненциальные функции. Теперь выражение для энергетической спектральной плотности, основанное на преобразовании Фурье выражения (1.3), имеет вид:
S( f ) |
|
ˆ |
|
2 |
(1.15) |
|
|
||||
|
X( f ) |
|
, |
где
P |
|
2 m |
|
(1.16) |
|
Xˆ ( f ) Am exp( j m ) |
|
. |
|||
m2 |
[2 ( f fm )]2 |
||||
m 1 |
|
|
Спектр, полученный по алгоритму Прони, обладает способностью получать узкополосные или широкополосные спектральные линии, форма кото-
16
рых зависит от величины коэффициента затухания. Кроме того, алгоритм Прони обеспечивает получение информации о фазе, которая теряется при спектральном АР-оценивании.
По сравнению с алгоритмом Писаренко, метод Прони имеет несколько преимуществ:
-не требуется получать оценки значений КФ;
-меньшее число ложных спектральных линий;
-меньшие значения смещений оценок частоты и мощности;
-отсутствуют боковые лепестки.
Кнедостаткам метода Прони можно отнести следующее:
-очень неточные оценки при малом отношении сигнал/шум;
-эти алгоритмы требуют больших вычислительных затрат, к тому же на каждом шаге вычисления требуется обращение матриц, размерность которых может быть равна числу имеющихся отсчетов данных;
-наилучшие оценки по методу Прони получаются, если входной процесс аппроксимируется суммой экспонент или затухающих синусоид;
-итеративные алгоритмы могут не сходиться к глобальному минимуму.
Отмеченные вычислительные сложности привели к разработке быстрых вычислительных алгоритмов для субоптимальных процедур минимизации квадратичной ошибки.
Рассмотрим еще один метод спектрального оценивания помеховой обстановки, основанный на адаптивных алгоритмах вычисления АРССпараметров с применением решетчатых структур.
Впринципе АР-процесс имеет три эквивалентных представления:
в виде бесконечно протяженной корреляционной последовательности
Rx(0), Rx(1),..., Rx(р),...;
в виде конечной последовательности авторегрессионных параметров a p1 ,a p2 ,..., a pp , 2p ;
в виде конечной последовательности коэффициентов отражения (решетчатая структура).
Методы адаптивной обработки сигналов, основанные на АРСС-модели, базируются на решении следующей задачи линейного предсказания.
Пусть YТ - скалярный, стационарный дискретный процесс с нулевым средним. Необходимо предсказать текущее значение этого процесса по данным измерений, проводимых ранее. Линейный фильтр предсказания порядка P , будет описываться соотношением
|
P |
|
|
УˆТ /Т 1 AP,iУТ i , |
(1.17) |
|
i 1 |
|
где Уˆ |
- предсказанное значение |
УТ по данным, полученным к моменту |
Т/Т 1
времени Т-1;
AP,i - коэффициенты фильтра предсказания. 17
Ошибка предсказания порядка P (разность между фактическим и предсказанным значением процесса) равна:
P,T УТ УˆТ /Т 1 |
|
P |
|
|
|
|
|
|
УТ |
AP,iУТ i. |
|
(1.18) |
|||||
|
|
|
i 1 |
|
|
|
|
|
Используя Z- преобразование, (1.18) можно записать в виде: |
||||||||
P,T AP(Z)УТ , |
|
|
|
|
|
|
(1.19) |
|
где A |
(Z ) 1 A ,Z 1 ... A Z |
P, Z 1У |
Т |
У |
Т |
1 |
. |
|
P |
P |
P,P |
|
|
|
|||
Оптимальный по критерию наименьших квадратов фильтр предсказания |
||||||||
минимизирует средний квадрат ошибки E{ P2 |
,T }. Коэффициенты AP,i такого |
|||||||
оптимального фильтра определяются статистиками процесса УТ второго порядка, то есть коэффициента корреляции {Ri, i=0, ..., P}, где Ri=E{УТУТ-i}.
Линейному фильтру предсказания отводится решающая роль в случае спектрального оценивания с высоким разрешением, адаптивного выделения спектральных линий, адаптивной компенсации шума и адаптивной обработки сигналов при классификации помеховой обстановки.
Если заданы АР-, СС- и АРСС – модели с конечным числом параметров, то одну из выбранных моделей можно выразить через две другие. Например, АРСС- и СС – процессы можно записать с помощью одной АР – модели в общем случае бесконечного порядка. Это позволяет выбирать любую из трех моделей и все же получать приемлемую аппроксимацию при достаточно большом порядке этой модели [64].
Из всех моделей временных рядов наибольшее внимание в технической литературе уделяется авторегрессионным спектральным оценкам, что объясняется двумя причинами:
1.АР – спектры имеют высокое разрешение.
2.Оценки АР – параметров можно получить как решения линейных уравнений (в отличие от оценок СС- и АРСС - параметров).
Дискретный процесс авторегрессии р–го порядка задается стохастическим разностным уравнением
p |
|
Y(n) akY n k n , |
(1.20) |
k 1 |
|
где Y(n) – наблюдаемое значение АР – процесса; ak – параметры АР – процесса; (n) – независимые величины с нулевым средним и дисперсией j2.
Вобщем случае АР-процесс имеет три эквивалентных представления:
в виде бесконечно протяженной корреляционной последовательности
Rx(0), Rx(1),..., Rx(р),...;
в виде конечной последовательности авторегрессионных параметров ap1,ap2 ,...,app, 2p;
18
в виде конечной последовательности коэффициентов отражения (решетчатая структура).
Передаточная функция системы, связывающая вход Хn и выход Yn для АРСС-процесса определяется рациональным выражением
|
B( z ) |
|
b |
b z 1 |
... b |
L |
z L |
|
|
|||
H( z ) |
|
|
|
|
0 |
1 |
|
|
, |
(1.21) |
||
A( z ) |
a |
|
a z 1 |
|
|
z L |
||||||
|
|
0 |
... a |
L |
|
|
||||||
|
|
|
|
|
1 |
|
|
|
|
|
||
где z – преобразования АР и СС частей процесса даются выражениями |
|
|||||||||||
|
p |
|
|
|
|
q |
|
|
|
|
|
|
A(z) am z m ; |
B(z) |
bm z m |
|
(1.22) |
||||||||
m 0 |
|
|
|
|
m 0 |
|
|
|
|
|
||
При построении цифровых фильтров существует, по меньшей мере, четыре вида его реализации или структур, которые могут быть использованы для адаптивной обработки сигналов: обычная, каскадная, параллельная и решетчатая.
Выражение (1.21) характерно для обычной структуры. Каскадную структуру получают из обычной – путем разложения на множители A(z) и
1 + B(z), а параллельную структуру – из каскадной путем раскрытия дроби. В большинстве случаев предполагается, что фильтр предсказания стро-
ится в прямой форме (в виде линии задержки с отводами), как показано на рисунке 1.1.
Такой фильтр содержит элементы задержки, выходы которых последовательно умножаются на весовые коэффициенты, формирующиеся в процессе адаптации, после чего полученные произведения суммируются.
Линейный фильтр предсказания, описываемый соотношением (1.20), можно интерпретировать как фильтр с конечной импульсной характеристикой (КИХ).
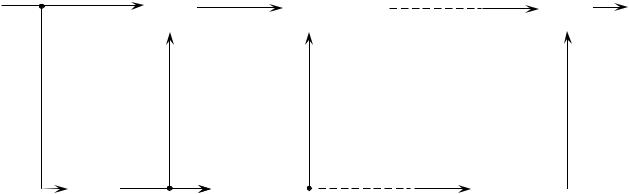
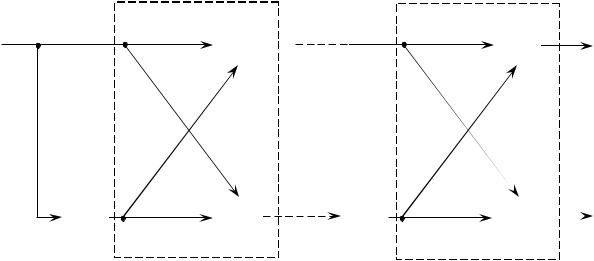
В определенных случаях фильтр предсказания реализуется в виде так называемой решетчатой или лестничной структуры (рисунок 1.2).
хT |
|
|
|
|
|
|
Р,T |
|
|
|
|
||||
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
A1,Т |
|
|
|
|
A2,Т |
|
|
|
|
|
AР,Т |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Z -1 |
хT -1 |
Z |
-1 |
|
|
|
|
Z |
-1 |
|
|
|
|
||
|
|
хT -2 |
|
|
|
|
хT -N |
|
|||||||
|
|
|
|
|
|||||||||||
Рисунок 1.1 – Прямая реализация КИХ-фильтра в виде линии задержки с отводами, работающего по критерию наименьших квадратов ошибок предсказания
19
0,T |
|
1,T |
Р-1,T |
|
|
|
Р,T |
|||
|
|
|||||||||
хT |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
||||
К1 |
|
|
|
|
КР |
|
|
|
||
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
К2 |
|
|
|
|
|
|
|
КР |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r0, |
Z |
-1 |
|
|
|
|
r1,T |
|
Z |
-1 |
|
|
|
|
rР,T |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
Рисунок 1.2 – Реализация фильтра на основе решетчатой структуры, работающий по критерию наименьших квадратов ошибок предсказания
Передаточная функция решетчатого фильтра определяется величинами параметров Кi, которые называются коэффициентами отражения или коэффициентами частичной корреляции. Значения коэффициентов отражения однозначно определяются передаточной функцией АN(Z) или, что эквивалентно, корреляционной последовательностью {Ri}.
Ошибки предсказания на n – ом временном шаге в р – ом каскаде прямой ( ) и обратной (r) ветвей решетчатой структуры определяются через ошибки на предыдущем каскаде рекуррентным образом:
0(n) = r0(n) = x(n); |
|
p(n) = p-1(n) + Kprp-1(n-1), 1 ≤ p P; |
(1.23) |
rp(n) = Kp p-1(n) + rp-1(n-1), |
|
где x(n) – входной процесс; p(n) – ошибки прямого предсказания; rp(n) – ошибки обратного предсказания решетчатой структуры.
Реализации фильтров в виде прямой и решетчатой структуры математически эквивалентны: между коэффициентами фильтров, показанных на рисунках 1.1 и 1.2, существует однозначное соответствие. Решетчатый фильтр (РФ) имеет более сложную структуру и требует большее количество математических операций. Тем не менее, решетчатые фильтры имеют ряд практических преимуществ.
1.В решетчатых фильтрах, в отличие от фильтров прямой структуры, можно не учитывать зависимость шума округления от ширины полосы и центральной частоты спектра обрабатываемых сигналов.
2.При одинаковых аппаратных ограничениях решетчатые фильтры обеспечивают в целом лучшие характеристики, чем при прямой реализации.
3.Решетчатый фильтр предсказания порядка N по критерию включает в себя фильтры предсказания всех более низких порядков. Таким образом, сиг-
20
