Нижние оценки на хроматическое число
•Определение. Кликовое число графа G – это количество вершин в наибольшей клике (полный подграф) графа G
•Утверждение. Хроматическое число любого графа G не может быть меньше его кликового числа.
•Тогда простой способ построения графа G с большим хроматическим числом поместить в граф G клику большого размера.
•Однако граф с большим хроматическим числом не обязательно имеет одновременно и большое кликовое число.
•Графы без треугольников – графы не содержащие простых циклов длины 3. Любой полный граф Kn (n ≥3) содержит в качестве своих подграфов клики любого размера Kk (k=1,..n-1) и, в частности, треугольник K3. Следовательно, графы без треугольников – это графы с кликовым числом ≤2.
Теорема (Мицельский, 1955). Для любого натурального k существует k-хроматический граф без треугольников.
Доказательство.
Рассмотрим в качестве примера 2-хроматический граф G2 = K2. Первая итерация описанной выше конструкции позволяет получить из него 3-хроматический граф G3 = C5. Следующая итерация, примененная к графу C5, дает нам так называемый граф Грётцша G4 .
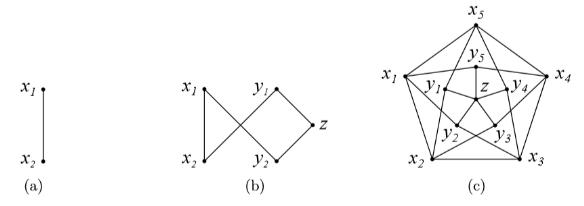
Покажем по индукции, что граф Грётцша G4, а также любые графы Gk+1, полученные в результате применения данной процедуры к графам Gk, являются (k + 1)-хроматическими графами без треугольников.
Заметим прежде всего, что граф Gk+1 не содержит никаких треугольников.
Действительно, так как все вершины множества Y несмежны друг с другом, то любой потенциальный треугольник в графе Gk+1 может содержать лишь одну вершину из множества Y . Как следствие, вершину z такой треугольник содержать уже не может. Поэтому единственный возможный вариант такого треугольника — это простой цикл вида xiyjxkxi.
Однако и это невозможно — в противном случае в исходном графе Gk существовал бы треугольник xixjxkxi, чего быть не может по индукционному предположению.
Теперь покажем, что граф Gk+1 является (k + 1)-раскра-шиваемым.
Для этого рассмотрим произвольную правильную окраску графа Gk в k цветов и продолжим ее на граф Gk+1 следующим образом: окрасим вершины yi графа Gk+1 в те же цвета, что и вершины xi, а вершину z окрасим в цвет (k + 1).
Осталось доказать, что граф Gk+1 не является k-раскра-шиваемым.
Предположим, что граф Gk+1 все же можно правильно окрасить в k цветов. Без потери общности мы можем считать, что вершина z окрашена в цвет k. При таком способе окраски никакая вершина множества Y не может быть окрашена в этот же цвет k. Перекрасим теперь каждую из вершин xi графа Gk в тот же цвет, в какой окрашена вершина yi. Так как множество смежных с xi вершин совпадает для любого i с множеством вершин, смежных с yi, то такой способ окраски графа Gk будет правильным. Однако этот способ окраски требует лишь (k - 1) цветов, что противоречит индукционному предположению.
Потоки. Величина потока, разрез графа, алгоритм Форда-Фалкерсона.