
Учебное пособие 800316
.pdf
Рис. 3.1
Двумя поперечными и одним цилиндрическим сечениями выделим из вала элемент (рис. 3.1) длиной dz и радиуса 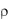 (ось
(ось
элемента совпадает с осью вала). Предположим, что до закручивания вала на рассматриваемый элемент нанесены радиальная OA и продольная AB риски. При закручивании риска OA повернется относительно своего прежнего положения на угол d , а риска AB на угол (это сдвиг, поскольку  пред-
пред-
ставляет собой происходящее при закручивании искажения прямого угла между риской AB и касательной к контуру поперечного сечения BC).
Имеем
AA |
d |
dz . |
|
|
Следовательно, |
|
|
|
|
|
d |
, |
(3.2) |
|
|
|
|
||
|
dz |
|||
|
|
|
||
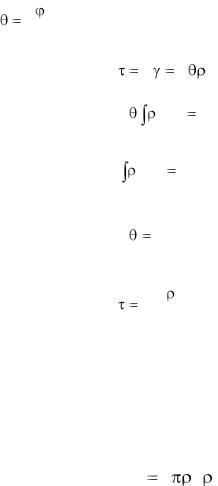
где |
|
d |
- относительный угол закручивания. |
|
||
|
|
|
||||
|
dz |
|
||||
По закону Гука |
|
|
|
|||
|
|
|
G |
G |
, |
(3.3) |
где G |
- модуль сдвига. Подставив (3.3) в (3.1), получаем |
|
||||
|
|
|
G |
2 dF |
M k . |
(3.4) |
|
|
|
F |
|
|
|
Величину
2 dF J p
F
называют полярным моментом инерции. Из (3.4) находим
G |
|
M k |
. |
(3.5) |
|
|
|
||||
|
|
J p |
|
|
|
и, следовательно, |
|
|
|
|
|
|
M k |
. |
(3.6) |
||
|
J p |
||||
|
|
|
|
||
Как видим, касательные напряжения изменяются вдоль радиуса по линейному закону.
3.1.3. Полярный момент инерции Определим полярный момент инерции для кольцевого по-
перечного сечения с внутренним радиусом r и наружным радиусом R (рис. 3.2). Выберем элементарную площадку и dF в виде кольца радиусом  и шириной d
и шириной d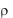 . Тогда
. Тогда
dF 2 d .
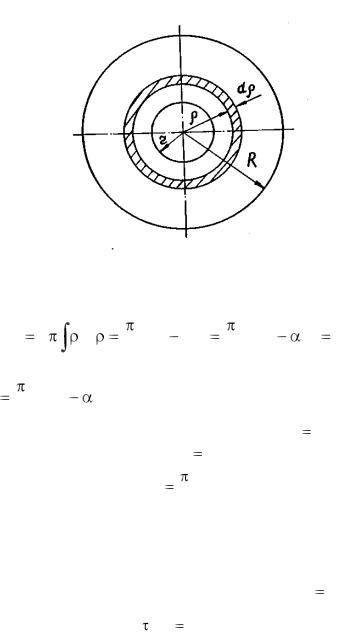
Рис. 3.2
Подставляя это соотношение в выражение для J p , получим
|
|
R |
|
|
|
|
R 4 |
|
||
|
|
|
3d |
|
(R4 |
r 4 ) |
4 ) |
|||
J p 2 |
|
|
(1 |
|||||||
2 |
2 |
|||||||||
|
|
r |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
||
|
D4 |
4 ), |
|
|
|
|
|
(3.7) |
||
|
|
(1 |
|
|
|
|
|
|
||
32 |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|||
где D=2R — наружный диаметр сечения; 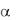 r
r R . В случае сплошного вала
R . В случае сплошного вала 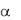 0 и, следовательно,
0 и, следовательно,
|
D 4 |
|
||
J p |
|
, |
(3.8) |
|
32 |
||||
|
|
|
||
где D - диаметр вала.
3.1.4. Условие прочности вала На рис. 3.3 в соответствии с (3.6) показана эпюра каса-
тельных напряжений в поперечном сечении вала. Наибольшее касательное напряжение возникает в точках  R
R
|
M k R |
. |
|
max |
J p |
||
|
|||
|
|
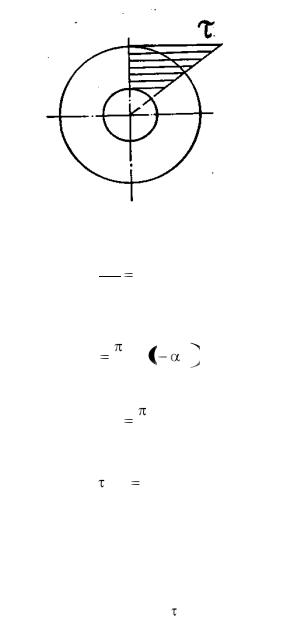
Рис. 3.3
Величину
J p
R Wp
называют полярным моментом сопротивления. В случае полого вала с учетом (3.7) получаем
|
D3 |
||
Wp |
|
1 4 . |
|
16 |
|||
|
|
||
В случае сплошного вала
|
|
D3 |
|
||
Wp |
|
|
. |
|
|
16 |
|
||||
|
|
|
|
||
Таким образом, |
|
|
|
|
|
|
|
M k |
|
||
max |
|
|
. |
(3.9) |
|
|
|||||
|
W p |
|
|||
|
|
|
|||
Поскольку в рассматриваемом случае возникает лишь одно напряжение, нет смысла привлекать к оценке прочности теории прочности. Целесообразнее определять предельное касательное напряжение испытанием материала на кручение. По этому предельному напряжению можно определить допускаемое касательное напряжение [ ], а условие прочности записать в виде
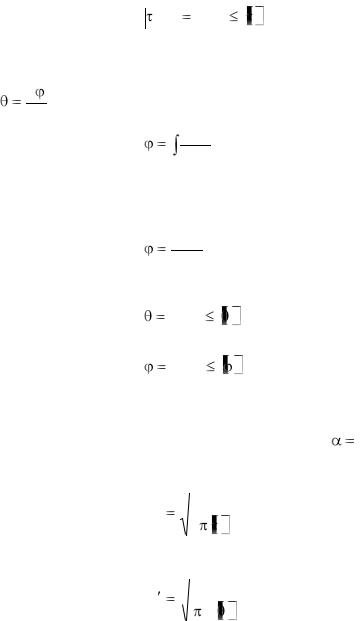
max |
|
|
M k |
(3.10) |
|
||||
|
|
|
||
|
|
Wp |
||
|
|
|
|
3.1.5. Условия жесткости вала Угол закручивания вала определим из (3.5) (учитывая, что
d ) dz
M k dz ,
l GJ p
где l - расстояние между сечениями, взаимный поворот которых определяется. Если между этими сечениями крутящий момент и поперечное сечение вала остаются постоянными, то
M k l . GJ p
Условия жесткости при кручении записывают в виде
M k |
, |
(3.11) |
||
GJ p |
||||
|
|
|
||
M k l |
|
. |
(3.12) |
|
GJ p |
|
|||
|
|
|
||
Пример. Сопоставить вес двух валов, изготовленных из одного материала и передающих одинаковый крутящий мо-
мент. Первый вал - сплошной, второй - полый с |
0,75 . |
Определим диаметр первого вала из условия прочности (3.10), взятого со знаком равенства
D1 |
3 |
16M k |
|
|
|
|
|
|
|
и из условия жесткости (3.11), также взятого со знаком равенства
D1 |
4 |
|
32M k |
|
|
G |
|
||
|
|
|
|
У полого вала
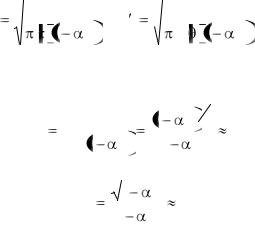
D2 |
3 |
16M k |
|
, D2 |
4 |
|
32M k |
|
|
1 |
4 |
|
G 1 |
4 |
|
||||
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
Отношение веса этих валов равно отношению их площадей поперечного сечения. Если диаметры валов определены из условия прочности, то
F1 |
|
|
2 |
|
1 |
4 |
23 |
|
|
|
D1 |
|
|
1,8 |
|||
F |
|
D 2 |
1 2 |
1 |
|
2 |
||
|
|
|
||||||
2 |
2 |
|
|
|
|
|
|
|
Если же диаметры определены из условия жесткости, то
|
|
|
|
|
|
|
F1 |
|
1 |
4 |
|
|
|
|
|
1,9 |
||||
F2 |
1 |
2 |
|
|||
|
|
|||||
|
|
|
||||
Как видим, вес полого вала значительно меньше веса сплошного вала. Объясняется это тем, что согласно эпюре касательных напряжений (рис. 3.3) в центральной части материал нагружен слабо и удаление материала в этой области не сказывается существенно на прочности и жесткости вала.
Однако стоимость полого вала далеко не всегда оказывается ниже стоимости сплошного вала. Расход материала при изготовлении полого вала меньше, но стоимость его изготовления может оказаться значительно выше стоимости изготовления сплошного вала.
4. ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПЛОСКИХ СЕЧЕНИЙ
4.1. Статические моменты сечений В курсе сопротивления материалов мы встречаемся с раз-
ными геометрическими характеристиками плоских сечений. В дальнейшем рассматривается ряд геометрических характери-
стик вида 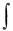 xa yb dF , где a и b - постоянные. Изучим их свой-
xa yb dF , где a и b - постоянные. Изучим их свой-
F
ства.
Статические моменты сечений, относительно осей x , y определяются соответственно интегралами вида
Sx |
ydF , |
S y |
xdF |
(4.1) |
|
F |
|
F |
|
При параллельном переносе осей координаты точек сече- |
||||
ния x1, y1 связаны с координатами x , y соотношениями |
|
|||
x1 |
x a, |
y1 |
y b, |
(4.2) |
где а и b - соответственно координаты x , y начала координат системы (рис. 4.1). В системе имеем
Sx |
y1dF |
( y b)dF Sx |
bF, |
|
1 |
|
|
|
|
F |
|
F |
|
|
S y |
x1dF |
(x b)dF S y |
aF |
(4.3) |
1 |
|
|
|
|
F |
|
F |
|
|

Рис. 4.1 4.2. Центр тяжести сечения
Оси, относительно которых статический момент равен нулю, называют центральными. Точка пересечения центральных осей называется центром тяжести сечения. Из (4.3) по-
лучим формулы для определения координат xc , yc центра тяжести, приравняв S x1 , S y1 нулю, а a, b - соответственно xc , yc
xc |
S y |
, yc |
Sx |
(4.4) |
|
F |
F |
||||
|
|
|
Из определения статических моментов следует, что статический момент сечения относительно некоторой оси можно определить как сумму статических моментов отдельных частей сечения при любом разбиении этого сечения на n частей относительно той же оси. Это позволяет переписать формулы (4.4) в виде
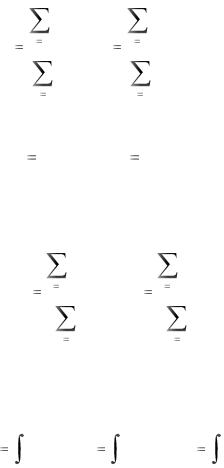
|
|
n |
|
|
|
|
n |
|
||||
|
|
|
|
S y i |
|
|
|
Sxi |
|
|||
|
xc |
i 1 |
|
, |
yc |
i |
1 |
|
|
|
||
|
n |
|
n |
|
||||||||
|
|
|
|
|
|
|
||||||
|
|
|
|
Fi |
|
|
|
Fi |
|
|||
|
|
i 1 |
|
|
i |
1 |
|
|
|
|||
Поскольку в соответствии с (4.4) |
|
|
|
|
||||||||
|
Sxi |
Fi yci , |
S yi |
|
Fi xci , |
|
||||||
г де xci , yci |
- координат ы центра тяжести i-ой части се чения |
|||||||||||
площадью Fi |
в системе координат |
x, y, можно записать |
||||||||||
|
|
|
|
n |
|
|
|
|
n |
|
||
|
|
|
|
Fi xci |
|
|
|
Fi yci |
|
|||
|
xc |
|
|
i 1 |
|
; |
yc |
|
i 1 |
. |
||
|
|
|
n |
|
|
|
n |
|||||
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
Fi |
|
|
|
|
|
Fi |
|
|
|
|
|
i 1 |
|
|
|
|
i 1 |
|
||
4.3. Моменты инерции сечения 4.3.1. Осевые и центробежный моменты инерции сечения
Рассмотрим интегралы
J x |
y 2 dF, J y |
x2 dF, J xy |
xydF. |
F |
F |
|
F |
Первый из них называют осевым моментом инерции сечения относительно оси x, второй - осевым моментом инерции сечения относительно оси y, тре-
тий - центробежным моментом инерции сечения относительно осей x, y. Легко увидеть, что осевые моменты всегда положительны, центробежный момент
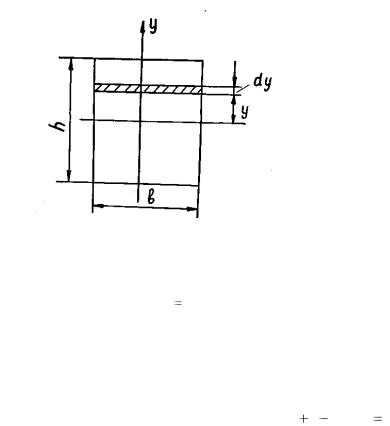
|
|
отрицатель- |
|
|
прямоугольного |
сечения |
|
.2). Начнем с |
|
|
элементарную |
|
|
|
Рис. 4.2
Аналогично
J y |
hb3 |
|
|
12 . |
|||
|
|||
Что же касается центробежного момента инерции J xy , то лег-
ко убедиться, что он равен нулю. Действительно, поскольку ось y является осью симметрии, каждой площадке dF с координатами x, y справа от оси соответствует такая же площадка слева от оси с координатами -x, y. Сумма xydF ( x) ydF 0. В силу этого центробежный момент инерции относительно осей, из которых хотя бы одна является осью симметрии сечения, равен нулю.
Моменты инерции "сложных" сечений обычно определяют, разбивая эти сечения на некоторые "простые" части (прямоугольники, круги, треугольники и т.д.), пользуясь известным свойством интегралов, как сумму моментов инерции этих частей. Уже в связи с этим необходимо знать, как изменяются моменты инерции при параллельном переносе и повороте осей.
