
Учебное пособие 800237
.pdfФГБОУ ВПО «Воронежский государственный технический университет»
Кафедра систем информационной безопасности
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
ккурсовому проектированию по дисциплине «Основы цифровой обработки сигналов» для студентов специальности 090302 «Информационная безопасность телекоммуникационных систем»
очной формы обучения
Воронеж 2014
Составители: канд. техн. наук П. Л. Савинский, канд. техн. наук О. В. Поздышева
УДК 004.415.2.031.43
Методические указания к курсовому проектированию по дисциплине «Основы цифровой обработки сигналов» для студентов специальности 090302 «Информационная безопасность телекоммуникационных систем» очной формы обучения / ФГБОУ ВПО «Воронежский государственный технический университет»; сост. П. Л. Савинский, О. В. Поздышева. Воронеж, 2014. 27 с.
Методические указания посвящены вопросам проектирования основных каскадов цифро-аналогового тракта преобразования сигналов. В ходе выполнения курсового проекта студенты должны приобрести необходимые практические навыки по основным методам цифровой обработки сигналов и закрепить на практике знания, полученные в лекционном курсе.
Методические указания подготовлены в электронном виде в текстовом редакторе MS Word 2013 и содержатся в файле Савинский _КП_ЦОС.pdf.
Ил. 5. Библиогр.: 7 назв.
Рецензент д-р техн. наук, проф.А. Г. Остапенко
Ответственный за выпуск зав. кафедрой д-р техн. наук, проф. А. Г. Остапенко
Издается по решению редакционно-издательского совета Воронежского государственного технического университета
© ФГБОУ ВПО «Воронежский государственный технический университет», 2014
1.КРАТКИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ ПО ПРОЕКТИРОВАНИЮ ЭЛЕМЕНТОВ
ЦИФРО-АНАЛОГОВОГО ТРАКТА
Сигналы могут быть обработаны с использованием аналоговых методов (аналоговой обработки сигналов), цифровых методов (цифровой обработки сигналов) или комбинации аналоговых и цифровых методов (комбинированной обработки сигналов) [1, 4].
Что касается цифровой обработки сигналов, то главное отличие его от традиционного компьютерного анализа данных заключается в высокой скорости и эффективности выполнения сложных функций цифровой обработки, таких как фильтрация, анализ с использованием быстрого преобразования Фурье (БПФ) и сжатие данных в реальном масштабе времени.
Термин «комбинированная обработка сигналов» подразумевает, что системой выполняется и аналоговая, и цифровая обработка. Такая система может быть реализована в виде печатной платы, гибридной интегральной схемы или отдельного кристалла с интегрированными элементами. АЦП и ЦАП рассматриваются как устройства комбинированной обработки сигналов, так как в каждом из них реализованы и аналоговые, и цифровые функции.
Сама природа ЦОС подразумевает, что эти функции могут быть выполнены в режиме реального масштаба времени.
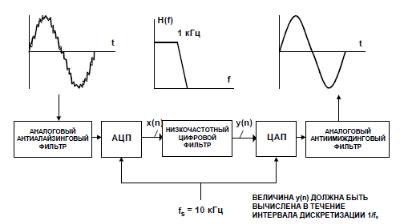
Цифровой фильтр, реализованный в виде типичной дискретной системы, показан на рис. 1. Для повышения эффективно-
сти устройства необходимо: во-первых, чтобы точно обработать сигнал, необходимо, чтобы тракт АЦП/ЦАП обладал достаточными значениями частоты дискретизации, разрешающей способности и динамического диапазона;во-вторых, для того, чтобы закончить все свои вычисления в пределах интервала дискретизации(1/fs), устройство ЦОС должно иметь достаточное быстродействие;в-третьих, на входе АЦП и выходе ЦАП сохраняется потребность в аналоговых фильтрах низкой ча-
стоты (anti-aliasingfilter и anti-imagingfilter), хотя требования к
их производительности невелики. Приняв эти допущения, можно сравнить цифровой и аналоговый фильтры.
Рис. 1. Цифровой фильтр, реализованный в виде типичной дискретной системы
1.1.Цифровые фильтры
Водномерной дискретной линейной системе связь между входом и выходом (входной и выходной дискретными последовательностями значений сигнала – отсчетами), задается линейным оператором преобразования TL [2]:
y(k t) = TL{x(k t)}.
Это выражение отображает краткую запись линейного разностного уравнения:
M m 0
N
am y(k t-m t) = bn x(k t-n t),
n 0
(1.1)
где k = 0,1,2,..-порядковый номер отсчетов, t -интервал дискретизации сигнала, am и bn- вещественные или, в общем случае, комплексные коэффициенты. Положим a0 = 1, что всегда может быть выполнено соответствующей нормировкой урав-
2
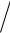
нения (1), и, принимая в дальнейшем t = 1, приведем его к виду:
y(k) =
N n 0
bnx(k-n) –
M m 1
am y(k-m).
(1.2)
Оператор, представленный правой частью данного уравнения, получил название цифрового фильтра (ЦФ), а выполняемая им операция - цифровой фильтрации данных (информации, сигналов). Если хотя бы один из коэффициентов am или bn зависит от переменной k, то фильтр называется параметрическим, т.е. с переменными параметрами.
Удобным методом решения разностных уравнений ли-
нейных систем является z-преобразование. Применяя z- преобразование к обеим частям равенства (1.1), c учетом сдвига функций (y(k-m) zm Y(z)), получаем:
Y(z)
M m 0
amzm = X(z)
N n 0
bnzn,
(1.3)
где X(z),Y(z)-соответствующие z-образы входного и выходного сигнала. Отсюда, полагая ao = 1, получаем в общей форме функцию связи выхода фильтра с его входом - уравнение пе-
редаточной функции системы в z-области:
N |
|
M |
H(z) = Y(z)/X(z) = bnzn |
(1+ |
|
n 0 |
|
m 1 |
Для НЦФ: |
|
|
N |
|
|
H(z) = bnzn. |
||
n 0 |
|
|
amzm).
(1.4)
(1.5)
При проектировании фильтров исходной, как правило, является частотная передаточная функция фильтра H(ω),по которой вычисляется ее Z-образ H(z)и обратным переходом в пространство сигналов определяется алгоритм обработки данных. В общей форме для выходных сигналов фильтра:
3
|
|
M |
Y(z) = H(z)·X(z). Y(z)·(1+ |
|
|
|
|
m 1 |
|
N |
|
Y(z) = X(z)· |
bn·zn |
|
|
n 0 |
|
|
|
N |
am·zm) = X(z)· |
|
|
|
|
n 0 |
|
M |
|
– Y(z)· |
am·zm. |
|
|
m 1 |
|
bn·zn
(1.6)
После обратного Z-преобразования выражения (1.6):
N |
M |
|
y(k) = bn·x(k-n) – |
am·y(k-m). |
(1.7) |
n 0 |
m 1 |
|
При подаче на вход фильтра единичного импульса Кро-
некера о, имеющего z-образ (z) = zn= 1, сигнал на выходе фильтра будет представлять собой импульсную реакцию фильтра y(k) ≡ h(k), при этом:
H(z) = Y(z)/ (z) = Y(z) = TZ[y(k)] =
k 0
h(k)zk, (1.8)
т.е. передаточная функция фильтра является z-образом ее им-
пульсной реакции. При обратном z-преобразовании передаточной функции соответственно получаем импульсную характеристику фильтра:
h(k) H(z). |
(1.9) |
Если функция H(z)представлена конечным степенным полиномом, что, как правило, характерно для НЦФ, то обрат-
ное z-преобразование осуществляется элементарно идентифи-
кацией коэффициентов по степеням z. Передаточная функция РЦФ также может быть представлена степенным полиномом прямым делением числителя на знаменатель правой части выражения (1.4), однако результат при этом может оказаться как
4
конечным, так и бесконечным, т.е. система может иметь либо конечную, либо бесконечную импульсную характеристику. Фильтры с бесконечной импульсной характеристикой получили название БИХ-фильтров, с конечной импульсной характеристикой соответственно КИХ-фильтров.
Фильтр называется устойчивым, если при любых начальных условиях реакция фильтра на любое ограниченное воздействие также ограничена. Критерием устойчивости фильтра является абсолютная сходимость отсчетов его импульсного отклика:
n |h(n)| < .
Анализ устойчивости может быть проведен по передаточной функции. В устойчивой системе значение H(z) должно
быть конечным во всех точках z-плоскости, где |z| 1, а, следовательно, передаточная функция не должна иметь особых
точек (полюсов) на и внутри единичного круга на z-плоскости.
Полюсы H(z) определяются корнями многочлена знаменателя передаточной функции (1.4).
Приведенный критерий устойчивости относится к несократимой дроби, т.к. в противном случае возможна компенсация полюса нулем передаточной функции, и следует проверить наличие однозначных нулей и полюсов.
Проверка на устойчивость требуется только для рекурсивных цифровых фильтров (систем с обратной связью), нерекурсивные системы всегда устойчивы.
От z-образов сигналов и передаточных функций подстановкой z = exp(-j t) в уравнение (1.4) можно перейти к Фурье-образам функций, т.е. к частотным спектрам сигналов и частотной характеристике фильтров, а точнее – к функциям их спектральных плотностей.
5

Передаточная частотная функция (частотная характеристика при ао=1):
N = n 0
H( ) = A( )/B( ) =
bnexp(-j n t) |
|
M |
[1+ |
am exp(-j m t)]. |
|
|
|
m 1 |
Нетрудно убедиться, что полученная частотная характеристика повторяет функцию (1.4) при z = exp(-j t), что и
следовало ожидать. Аналогично z-преобразованию (1.9), частотная характеристика фильтра представляет собой Фурьеобраз его импульсной реакции, и наоборот. При t = 1:
H( ) =
n
h(n) exp(-j n),
h(n) = (1/2 )
π - π
H( ) exp(j n) d .
В общем случае H( ) является комплексной функцией, модуль которой R( ) называется амплитудно-частотной ха-
рактеристикой (АЧХ), а аргумент ( ) -фазочастотной характеристикой (ФЧХ).
|
Re |
2 |
H ( ) Im |
2 |
H ( ) |
|
|
|
|
( ) = arctg(-Im H( )/Re H( )).
На рис. 2 приведен пример частотных характеристик фильтра (модуль и аргумент спектральной плотности).
6
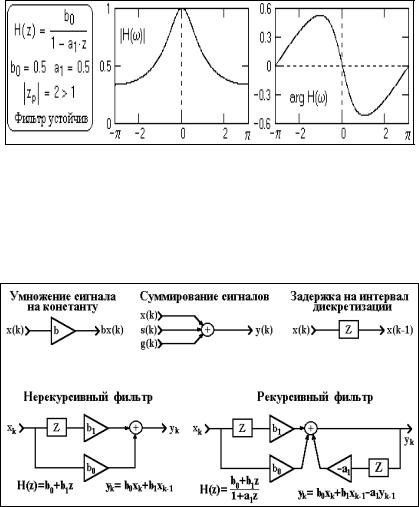
Рис. 2. Спектр не имеет особых точек
Алгоритмы цифровой фильтрации сигналов (цифровых фильтров) представляются в виде структурных схем, базовые элементы которых показаны на рис. 3 вместе с примерами структурных схем фильтров.
Рис. 3. Структурные схемы цифровых фильтров
7
1.2. Явления Гиббса
Чаще всего с изменением частотных характеристик функций приходится сталкиваться при усечении операторов фильтров. На примере усечения операторов и рассмотрим характер происходящих изменений [2].
При расчетах фильтров, как правило, задается определенная передаточная характеристика H( ) фильтра и по ней производится расчет оператора фильтра h(n), количество членов которого может оказаться очень большим даже только по
значимым значениям. Усечение может рассматриваться, как результат умножения функции оператора фильтра на селектирующее весовое окно длиной 2N+1. В простейшем случае это окно представляет собой П-образную селектирующую функцию:
hn= h(n)·ПN(n),
, при | | ≤ , где ПN(n) = { , при | | > .
Функция h(n)оператора фильтра, в пределе бесконечная, обуславливает определенную частотную передаточную характеристику фильтра H( ). Полному оператору h(n) соответствует исходная частотная характеристика H( ):
|
|
|
H( ) = |
h(n) exp(-j n). |
(1.10) |
n
Сущность явления Гиббса. Функции во временном окне селекции ПN(n) в частотном пространстве соответствует спектральная функция, которая в определенной степени должна отличаться от функции H( Очевидно, что при усечении оператора h(n),а значит и ряда Фурье (1.10), до конечного числа членов N мы будем иметь усеченный ряд Фурье:
N
HN( ) = h(n) exp(-j n), (1.11)
n - N
8
