5. Частные производные функции нескольких

ПЕРЕМЕННЫХ

Определение. Частной производной по от функции называется предел отношения частного приращения по к приращению при стремлении к нулю (если он существует)

Аналогично,

Заметим, что вычисляется при неизменном , а

при неизменном , поэтому частной производной по от функции является производная по , вычисленная в предположении, что - постоянная.

Частной производной по от функции является производная по , вычисленная в предположении, что - постоянная.

Частной эластичностью функции нескольких переменных относительно переменной называется величина .

Значение показывает приближенно, на сколько процентов изменится переменная z при изменении переменной на 1%.

Примеры.

1.Найти частные производные функций:

1.1. .

Решение. Вычислим в предположении, что имеет

фиксированное значение: . При вычислении считаем, что имеет фиксированное значение, тогда

1.2. , .

Решение. При вычислении частной производной функции

по аргументу рассматриваем функцию как функцию только одной переменной , то есть считаем, что имеет фиксированное значение. При фиксированном функция является степенной функцией аргумента . По формуле дифференцирования степенной функции получаем Аналогично, при вычислении частной производной считаем, что фиксировано значение , и рассматриваем функцию как показательную функцию аргумента .

Получаем

2. Поток пассажиров z выражается функцией , где х – число жителей; у - расстояние между городами. Найти частные производные этой функции и пояснить их смысл.

Решение. Производная показывает, что при одном и том же расстоянии между г7ородами увеличение потока пассажиров пропорционально удвоенному числу жителей. Производная показывает, что при одной и той же численности жителей увеличение потока пассажиров обратно пропорционально квадрату расстояния между городами.

Задачи для самостоятельной работы:

Найти частные производные следующих функций:

1. 2. 3.

4. 5. 6.

7. 8. 9. 10.

6. ПРОИЗВОДНАЯ ПО НАПРАВЛЕНИЮ. ГРАДИЕНТ

Пусть функция определена в некоторой окрестности точки , - некоторое направление, задаваемое единичным вектором , где - косинусы углов, образуемых вектором с осями координат и называемые направляющими косинусами. Пусть -фиксированная точка; - любая точка из , отличная от и такая, что вектор коллинеарен . Пусть, далее, - величина направленного отрезка ( она равна его длине , если векторы и сонаправлены, и равна - , если эти векторы противоположно направлены)

Определение. Производной по направлению функции двух переменных называется предел отношения приращения функции в этом направлении к величине перемещения при стремлении последней к нулю, то есть

=

Производная по направлению характеризует скорость изменения функции по направлению в точке .

Если в прямоугольной системе координат функция , а , то

В частности, если вектор сонаправлен с одной из координатных осей, то производная по направлению совпадает с соответствующей частной производной. Например,

если , то

Определение. Градиентом функции называется вектор-функция

Из равенства следует, что , откуда, ,

так как =1. Здесь - угол между векторами и в точке . Очевидно, что принимает наибольшее значение при , то есть в направлении в данной точке.

Таким образом, вектор в данной точке указывает направление максимальной скорости изменения функции в этой точке, а есть скорость роста функции в этом направлении.

Пример 6.1. Найти производную функции в точке А(2,1,1) по направлению к точке В(2,4,-3).

Решение. 1. Функция дифференцируема в точке А(2,1,1), поэтому в этой точке существует ее производная по любому направлению , которая определяется формулой .

2. Находим координаты вектора . В данном случае

3.Находим единичный вектор (орт) :

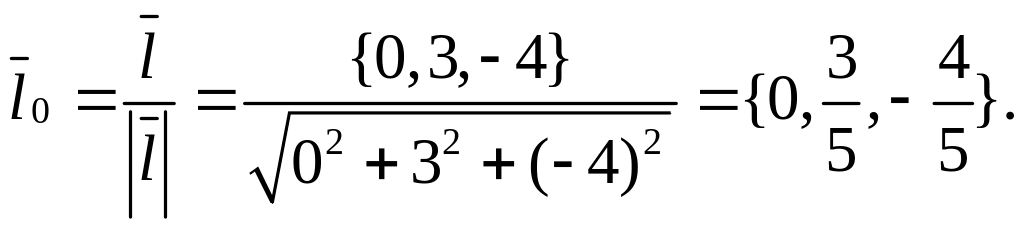
4. Вычисляем частные производные функции в точке А(2,1,1):

Тогда

5. Подставляя полученные значения в формулу , получим

Задачи для самостоятельной работы

1. Найти градиент функции в точке М.

1.1.

1.2.

1.3.

1.4.

1.5.

1.6.

2. Найти угол между градиентами скалярного поля в точках и

3. Найти производную функции в точке А по направлению к точке В.

3.1.

3.2.

3.3.

3.4.

3.5.

3.6.

7. ПОЛНЫЙ ДИФФЕРЕНЦИАЛ ФУНКЦИИ

НЕСКОЛЬКИХ ПЕРЕМЕННЫХ

Определение. Функция , полное приращение

которой в данной точке может быть представлено в виде суммы выражения, линейного относительно и величины бесконечно малой более высокого порядка, чем , называется дифференцируемой в данной точке.

Главная часть полного приращения функции линейная относительно называется полным дифференциалом функции и обозначается или .

Если функция имеет непрерывные частные производные в данной точке, то она дифференцируема в этой точке и имеет полный дифференциал

.

Полное приращение функции представимо в виде .

Приращения будем называть дифференциалами независимых переменных и обозначать , тогда

.

Аналогично, для функции трех переменных полный дифференциал равен

Пример 7.1. Найти полный дифференциал функции

в точках

Решение. Вычислим частные производные

. Запишем вид дифференциала

Тогда

Задачи для самостоятельной работы

Найти полные дифференциалы функций:

1. . 2.

3. 4.

5. 6.

7. 8.

9.Найти полный дифференциал функций:

в точках .

8. ПРИМЕНЕНИЕ ПОЛНОГО ДИФФЕРЕНЦИАЛА К

ПРИБЛИЖЕННЫМ ВЫЧИСЛЕНИЯМ

Из формулы следует, что , тогда , следовательно,

.

Пример 8.1. Вычислить приближенно .

Решение. Пусть , , Найдем

.

Вычислим

Задача для самостоятельной работы

Вычислить приближенно

1. . 2. 3.

Ответ: 1. 8,29. 2. 0,97. 3. 4,998.