15. Первый замечательный предел
Во многих случаях используется
первый замечательный предел
(х- длина дуг или угол, выраженный в
радиана х) и предполагается известным,
что
.
Иногда при отыскании предела полезно
сделать замену переменной с
тем, чтобы упростить вычисление предела
и использовать известные пределы. Если
пол знаком предела делается замена
переменной, то все величины, находящиеся
под знаком, должны быть выражены через
эту новую переменную. Из равенства,
выражающего зависимость между старой
переменной и новой, надо определить
предельное значение новой переменной.
Например,
при нахождении предела
обозначаем
t=kx
, где при
новая переменная
,
x=t/k. Тогда
(т.к.cos
(0)=1). Полезно
помнить, что
, где k
-постоянная величина. Например, при
функция sin(x)
и tg(x)
эквивалентные
бесконечно
малые, т.е. sin(x)~tg(x);
т.к.
.
Пример
. Найти
Решение. Применим сначала формулу тригонометрии
1-cos(t)=2sin2(t/2).
У нас
1-cos(kx)=2sin2(kx/2),
при
;
sin2(
)~(
)2.
По теореме “замены эквивалентной” получим
.
Заметим, что можно было воспользоваться первым замечательным пределом.
Ответ: k2/2.
Решение типовых задач на вычисление предела функций.
Пример.
Вычислить
Решение. По формуле тригонометрии
sin(5(x+π))= sin(5x+5π)=- sin(5x).
Тогда
Поскольку при , sin(5x)~5x, e3x-1~ 3x. Ответ:-5/3.
16. Вычисление предела показательно-степенной функции
При
нахождении пределов вида
=C
Следует иметь ввиду, что:
1) если существуют конечные пределы
и
,
то C=AB,
т.е.
имеет
место формула
Заметим,
что предельное значение а может
обозначать и число, и один из символов
;
2)
если
и
,
то вопрос о нахождении затруднений обычно не вызывает. В том случае полезны иногда формулы:
;
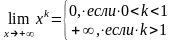3)
если
и
,
т.е. имеем неопределенность вида {
},
то полагают
,
где
при
и,
следовательно,
Проиллюстрируем общий прием вычисления таких пределов на следующем примере ( раскрытие неопределенности вида { }).
Пример.
Найти
Решение.
Здесь
основание степени
при
,а
показатель степени
,
т.е. имеется неопределенность вида
.
Тогда
.
(Получили
в качестве
при
).
Замечание
1. При
вычислении пределов выражений вида
,где
,
при
,
удобно иногда пользоваться формулой
.
Замечание 2. При вычислении пределов полезно знать, что
а)
если существует и положителен
,
то
;
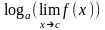б)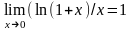
;
в)
.
17. Производная функции и ее вычисление
Если
х и
х1
– значения
аргумента х,
а y=f(x)
и y=f(x1)
- соответственно значения функции y=f(x)
,
то называется приращением
аргумента х
на отрезке
[x;
х1],
а
(или
=
)
называется приращением функции на том
же отрезке [x;
х1],
(см. рисунок), где
).
Рис. 6
Отношение
называется средней скоростью
изменения
функции y=f(x)
на отрезке
.
Производной
функции
y=f(x)
в точке x
называется предел отношения приращения
функции
к приращению аргумента
, когда приращение аргумента стремится
к нулю:
=
,
если этот
предел существует.
Геометрический
смысл производной:
=tg
-
угловой коэффициент касательной МТ
к графику функции y=f(x)
в точке х
(рис. 6).
Физический
смысл производной
-
мгновенная скорость, т.е. скорость
изменения функции в данный момент х0.
Таким образом, быстрота протекания
физических, химических и других процессов
выражается с помощью производной.
Функция, имеющая конечную производную, называется дифференцируемой. Операция нахождения производной называется дифференцированием.
Основные правила дифференцирования.
Если
,
- функции, имеющие производные, c-
постоянная величина, то:
1)
(c=const);
2)
;
3)
;
4)
;
5)
;
6)
; 7)
.