- •Методические указания
- •Часть 1
- •Методические указания
- •Часть 1
- •Лабораторная работа № 1 табулирование функции на интервале. Построение графика функции
- •Контрольные вопросы
- •Содержание отчета
- •Лабораторная работа № 3 приближенноевычисление определенных интегралов
- •Контрольные вопросы
- •Содержание отчета
- •Содержание
- •Часть 1
- •394026 Воронеж, Московский просп.,14
Контрольные вопросы
1. Как убедиться в том, что на отрезке имеются только один корень уравнения?
2. Опишите аналитический процесс нахождения корня методом касательных.
3. Дайте геометрическую интерпретацию метода для разных вариантов поведения функции: возрастающей, убывающей, вогнутой, выпуклой.
4. Как определить, в каком из концов дуги графика функции проводить касательную для получения приближения к корню?
5. Как оценить погрешность приближенного значения корня?
6. Как влияют численные значения первой и второй производной функции на скорость вычисления корня?
Содержание отчета
Отчет должен содержать постановку задачи, расчетную формулу, нахождение производных и вычисление их значений, проверку достаточных условий сходимости метода, обоснование выбора начального приближения, текст программы, вычисленные приближенные значения корня и соответствующие погрешности после каждой итерации.
Лабораторная работа № 3 приближенноевычисление определенных интегралов
Задание.
Вычислить интеграл
 методами
методами
прямоугольников, трапеций и Симпсона с точностью
Краткое
описание методов: Вычисление
интеграла будем проводить параллельно
по трем формулам: прямоугольников,
трапеций и Симпсона. Процесс вычислений
будет закончен, когда требуемая точность
будет достигнута по одной из формул.
При этом отрезок интегрирования
первоначально разбивается на две равные
части, а в последующей итерации число
разбиений n увеличивается
в два раза. В
методе
прямоугольников
площадь элементарной криволинейной
трапеции приближенно заменяется площадью
прямоугольника. Методы прямоугольников
бывают трех видов:
метод
центральных прямоугольников, метод
левых прямоугольников и метод правых
прямоугольников.
В данной работе используется метод
левых прямоугольников, геометрическая
иллюстрация которого приведена на рис.
3. Соответствующая формула имеет вид
 ,
где
,
где

 – величина шага разбиения отрезка
– величина шага разбиения отрезка
 .
.

ВВ
методе
трапеций
площадь элементарной криволинейной
трапеции приближенно заменяется площадью
трапеции. Геометрическая иллюстрация
метода приведена на рис. 4. Соответствующая
формула для площади элементарной
криволинейной трапеции имеет вид
 .
Тогда вся площадь фигуры под кривой
.
Тогда вся площадь фигуры под кривой


В методе
Симпсона
(методе парабол)
площадь элементарной криволинейной
трапеции заменяется площадью фигуры,
расположенной под параболой. Так как
число элементарных отрезков разбиения
четно, то в качестве элементарного
отрезка используется отрезок длины 2h
(рис.5). В
методе
Симпсона
(методе парабол)
площадь элементарной криволинейной
трапеции заменяется площадью фигуры,
расположенной под параболой. Так как
число элементарных отрезков разбиения
четно, то в качестве элементарного
отрезка используется отрезок длины 2h
(рис.5). В
этом случае формула Симпсона имеет вид:
 X
X
Отметим также, что формулы левых и правых прямоугольников имеют первый порядок точности относительно h, формулы центральных прямоугольников и трапеций имеют второй порядок точности, а формула Симпсона - четвертый порядок точности.
Варианты исходных данных
Ва- ри- ант |
Интеграл |
Ва- ри ант |
Интеграл |
1 |
|
13 |
|
2 |
|
14 |
|
3 |
|
15 |
|
4 |
|
16 |
|
5 |
|
17 |
|
6 |
|
18 |
|
7 |
|
19 |
|
8 |
|
20 |
|
9 |
|
21 |
|
10 |
|
22 |
|
11 |
|
23 |
|
12 |
|
24 |
|
Схема алгоритма метода.

Алгоритм программы
Задание констант а, b и ;
описание переменных х, Qn, Qs, h, Sp, St, SS, d, k, n;
описание подынтегральной функции
 ;
начало исполняемой части программы
;
начало исполняемой части программы


повторять

повторять
|

до выполнения условия


повторять
|

до выполнения условия

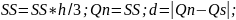
вывод на экран номера итерации k и значения Sp, St и SS с семью цифрами после запятой; до выполнения условия
 .
.
конец программы.
Контрольные вопросы
1. В чем состоит метод левых прямоугольников?
2. В чем состоит метод центральных прямоугольников?
3. В чем состоит метод трапеции?
4. В чем состоит метод Симпсона?
5. Какой из рассмотренных методов точнее и почему?
Содержание отчета
Отчет должен содержать постановку задачи, расчетные формулы, текст программы и результаты расчетов, выведенные на экран.
ЛАБОРАТОРНАЯ РАБОТА № 4
РЕШЕНИЕ СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ МЕТОДОМ ГАУССА С ВЫБОРОМ ГЛАВНОГО ЭЛЕМЕНТА
Задание. Решить систему линейных алгебраических уравнений методом Гаусса с точностью до 0,001, а также найти определитель матрицы этой системы.
Краткое описание метода
Методом
Гаусса называют
точный метод решения невырожденной
системы
(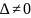 )
линейных алгебраических уравнений,
состоящий в том, что последовательным
исключением неизвестных систему
)
линейных алгебраических уравнений,
состоящий в том, что последовательным
исключением неизвестных систему
 ………(4.1)
………(4.1)
приводят к эквивалентной системе с треугольной матрицей

решение которой, находят по рекуррентным формулам

Существует много вариантов этого метода.
Рассмотрим схему
с выбором главного элемента.
Предположим, что в исходной системе
(4.1)
 ,
и разделим обе части первого уравнения
системы на
,
и разделим обе части первого уравнения
системы на
 В результате получим
В результате получим

где
 С помощью уравнения (4.3) исключим во всех
уравнениях системы (4.1), начиная со
второго, слагаемые, содержащие
.
Для этого умножаем обе части уравнения
(4.3) последовательно на
С помощью уравнения (4.3) исключим во всех
уравнениях системы (4.1), начиная со
второго, слагаемые, содержащие
.
Для этого умножаем обе части уравнения
(4.3) последовательно на
 и
вычитаем
соответственно из второго, третьего,
…,
п-го уравнения
системы (4.1). В результате получаем
систему, порядок которой на единицу
меньше порядка исходной системы:
и
вычитаем
соответственно из второго, третьего,
…,
п-го уравнения
системы (4.1). В результате получаем
систему, порядок которой на единицу
меньше порядка исходной системы:
 ,
где
,
где

В результате n-кратного
повторения этого преобразования получим
систему (4.2) с треугольной матрицей,
которая эквивалентна системе (4.1) и легко
решается следующим образом. Из последнего
уравнения находим
 ,
подставляя
в предпоследнее уравнение, найдем
,
подставляя
в предпоследнее уравнение, найдем
 ,
затем
,
затем
 и т.д. до
.
находим из первого уравнения системы.
Таким образом, вычисления по методу
Гаусса распадаются на два этапа: на
первом этапе, называемом
прямым ходом метода Гаусса,
исходную систему преобразуют к
треугольному виду. На втором этапе,
который называют
обратным ходом, решают
треугольную систему (4.2), эквивалентную
исходной. Коэффициенты
и т.д. до
.
находим из первого уравнения системы.
Таким образом, вычисления по методу
Гаусса распадаются на два этапа: на
первом этапе, называемом
прямым ходом метода Гаусса,
исходную систему преобразуют к
треугольному виду. На втором этапе,
который называют
обратным ходом, решают
треугольную систему (4.2), эквивалентную
исходной. Коэффициенты
 называют
ведущими элементами метода
Гаусса. На каждом шаге предполагалось,
что
называют
ведущими элементами метода
Гаусса. На каждом шаге предполагалось,
что
 .
Если окажется, что это не так, то в
качестве ведущего элемента можно
использовать любой другой ненулевой
коэффициент системы. Однако, если
коэффициент
.
Если окажется, что это не так, то в
качестве ведущего элемента можно
использовать любой другой ненулевой
коэффициент системы. Однако, если
коэффициент
 мал, то после деления на этот элемент и
вычитания
k-го
уравнения из последующих возникают
большие погрешности округления. Чтобы
избежать этого, на каждом этапе уравнения
переставляют так, чтобы на главной
диагонали оказался наибольший по модулю
элемент
k-го
столбца. Если матрица системы хорошо
обусловлена, то в методе Гаусса с выбором
главного элемента погрешности округления
невелики. Одновременно с решением
системы можно найти определитель матрицы
системы. Нетрудно убедиться, что
определитель матрицы системы равен
произведению ведущих элементов, т.е.
мал, то после деления на этот элемент и
вычитания
k-го
уравнения из последующих возникают
большие погрешности округления. Чтобы
избежать этого, на каждом этапе уравнения
переставляют так, чтобы на главной
диагонали оказался наибольший по модулю
элемент
k-го
столбца. Если матрица системы хорошо
обусловлена, то в методе Гаусса с выбором
главного элемента погрешности округления
невелики. Одновременно с решением
системы можно найти определитель матрицы
системы. Нетрудно убедиться, что
определитель матрицы системы равен
произведению ведущих элементов, т.е.
 При этом необходимо учесть изменение
знака определителя при перестановке
строк.
При этом необходимо учесть изменение
знака определителя при перестановке
строк.
Варианты исходных данных
1 13 |
|
7 19 |
|
2 14 |
|
8 20 |
|
3 15 |
|
9 21 |
|
4 16 |
|
10 22 |
|
5 17 |
|
11 23 |
|
6 18 |
|
12 24 |
|
Схема алгоритма метода.

Алгоритм программы
Задание константы n;
описание переменных a, x, max_a, b, det, s, i, j, k, i_max, znak;
начало исполняемой части программы
задание значений коэффициентов системы; znak=1; det=1;
начало цикла по k от 1 до n-1 max_a=0; i_max=k;
в
цикле по i
oт
k
до n
если
 , то
, то
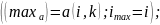
если
 то:
то:
начало цикла по j от k до n+1 b=a(k,j); a(k,j)=a(i_max,j); a(i_maax,j)=b
конец цикла по j;
znak=-znak;
det=det*a(k,k);
в цикле по j от n+1 до k a(k,j)=a(k,j)/a(k,k);
в цикле по i от k+1 до n в цикле по j от n+1 до k
a(i,j)=a(i,j)-a(i,k)*a(k,j)
конец цикла по k
det=det*a(n,n)*znak; вывод значения определителя;
в цикле по j от n+1 до n a(n,j)=a(n,j)/a(n,n);
x(n)=a(n,n+1)
начало цикла по i от n-1 до 1
s=0; в цикле по j от i+1 до n s=s+a(i,j)*x(j);
x(i)=a(i,n+1)-s
конец цикла по i; в цикле по i от 1 до n вывод x(i) с тремя цифрами после запятой
конец программы.
Контрольные вопросы
1. В чем состоит суть метода Гаусса?
2. Какие преобразования системы производят на первом этапе (прямой ход метода Гаусса)?
3. Какие действия производят на втором этапе (обратный ход метода Гаусса)?
4. Что означает выбор главного (ведущего) элемента и зачем он выполняется?
5. Как находится определитель матрицы системы?
Содержание отчета
Отчет должен содержать постановку задачи; формулы, применяемые для решения задачи;
текст программы и результаты расчетов.
ЛАБОРАТОРНАЯ РАБОТА № 5
АППРОКСИМАЦИЯ ФУНКЦИИ ПО МЕТОДУ НАИМЕНЬШИХ КВАДРАТОВ
Задание.
По данным значениям ,
вычислить коэффициенты аппроксимирующей
функции
,
вычислить коэффициенты аппроксимирующей
функции
 ,
протабулировать ее, сопоставить ее
значения с исходными данными и построить
график.
,
протабулировать ее, сопоставить ее
значения с исходными данными и построить
график.
Краткое описание метода
Очень часто, особенно при анализе эмпирических данных, возникает необходимость найти в явном виде функциональную зависимость между величинами х и у, которые получены в результате измерений. Как правило, общий вид этой функциональной зависимости известен, а некоторые числовые параметры закона неизвестны. В данной лабораторной работе заданную табличную функцию (число точек n=10) требуется аппроксимировать многочленом второй степени.

Согласно методу
наименьших квадратов
коэффициенты многочлена у(х)
нужно выбрать такими, чтобы сумма
квадратов отклонений
di
(рис. 6) многочлена от заданных значений
функции была минимальной. Другими
словами, коэффициенты
а,
b
и
с должны
минимизировать функцию
 . В точке минимума функции
F
ее производные
. В точке минимума функции
F
ее производные
 обращаются в нуль. Дифференцируя
F
и приравнивая нулю производные, получим
так называемую
нормальную
систему:
обращаются в нуль. Дифференцируя
F
и приравнивая нулю производные, получим
так называемую
нормальную
систему:
 ,
,
где A0=n=10,
 ,
,
 ,
,
 ,
,
 ,
, ,
,
 ,
,
 .
. Эта система хорошо обусловлена, и ее
можно решать методом Гаусса без выбора
главных элементов. Однако при степени
многочлена порядка 5 и выше нормальная
система становится плохо обусловленной
и погрешности определения коэффициентов
велики. Поэтому в настоящее время в
серьезной вычислительной практике
нормальная система, как правило, не
используется.
Эта система хорошо обусловлена, и ее
можно решать методом Гаусса без выбора
главных элементов. Однако при степени
многочлена порядка 5 и выше нормальная
система становится плохо обусловленной
и погрешности определения коэффициентов
велики. Поэтому в настоящее время в
серьезной вычислительной практике
нормальная система, как правило, не
используется.
Варианты исходных данных
|
Значения x (для всех вариантов) |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
||||||||||||||||
|
i |
Значение функции
|
|
|||||||||||||||||||||||
|
Вари-ант 1 |
Вари-ант 2 |
Вари-ант 3 |
Вари-ант 4 |
Вари-ант 5 |
Вари-ант 6 |
|
|||||||||||||||||||
|
1 |
9,987 |
2,707 |
7,408 |
7,274 |
2,076 |
8,688 |
|
||||||||||||||||||
|
2 |
9,529 |
1,672 |
7,862 |
4,762 |
3,716 |
7,103 |
|
||||||||||||||||||
|
3 |
9,957 |
2,100 |
8,845 |
4,262 |
5,642 |
6,190 |
|
||||||||||||||||||
|
4 |
9,358 |
2,072 |
8,617 |
2,999 |
6,356 |
4,912 |
|
||||||||||||||||||
|
5 |
8,884 |
2,741 |
9,228 |
3,012 |
7,788 |
4,902 |
|
||||||||||||||||||
|
6 |
7,473 |
3,045 |
7,888 |
2,986 |
7,996 |
4,010 |
|
||||||||||||||||||
|
7 |
6,839 |
4,696 |
7,439 |
4,275 |
8,863 |
4,017 |
|
||||||||||||||||||
|
8 |
4,706 |
5,420 |
5,749 |
5,211 |
8,560 |
3,992 |
|
||||||||||||||||||
|
9 |
3,061 |
7,204 |
4,289 |
7,314 |
9,303 |
4,649 |
|
||||||||||||||||||
|
10 |
0,664 |
8,787 |
1,456 |
8,896 |
8,043 |
4,843 |
|
||||||||||||||||||
i |
Значение функции полученные экспериментально |
|
|
|||||||||||||||||||||||
Вари-ант 7 |
Вари-ант 8 |
Вари-ант 9 |
Вари-ант 10 |
Вари-ант 11 |
Вари-ант 12 |
|
|
|||||||||||||||||||
1 |
5,208 |
6,930 |
10,640 |
3,281 |
7,258 |
7,022 |
|
|
||||||||||||||||||
2 |
6,462 |
4,912 |
10,440 |
2,507 |
7,912 |
5,034 |
|
|
||||||||||||||||||
3 |
8,245 |
4,143 |
10,950 |
3,024 |
9,095 |
4,551 |
|
|
||||||||||||||||||
4 |
8,817 |
2,769 |
10,160 |
2,804 |
9,067 |
3,545 |
|
|
||||||||||||||||||
5 |
10,230 |
2,998 |
9,612 |
3,398 |
9,878 |
3,568 |
|
|
||||||||||||||||||
6 |
9,688 |
1,770 |
8,727 |
4,227 |
8,738 |
4,039 |
|
|
||||||||||||||||||
7 |
10,040 |
2,353 |
7,635 |
5,420 |
8,489 |
5,090 |
|
|
||||||||||||||||||
8 |
9,149 |
1,916 |
6,127 |
6,770 |
6,999 |
6,511 |
|
|
||||||||||||||||||
9 |
8,489 |
2,562 |
4,643 |
8,614 |
5,739 |
8,641 |
|
|
||||||||||||||||||
10 |
6,459 |
2,854 |
2,334 |
10,410 |
3,109 |
10,930 |
|
|
||||||||||||||||||
Схема алгоритма метода.
 Алгоритм
программы
Алгоритм
программы
Описание переменных m, y, a, b, c, y1, d, y2, i, j, k, dr, reg, mx, my, s;
Начало исполняемой части программы
задание экспериментальных значений
 ;
;
в цикле по i от 1 до 3 в цикле по j от 1 до 4 выполнять обнуление элементов матрицы нормальной системы m(i,j)=0;
начало цикла по i от 1 до 10
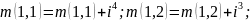



конец цикла по i

 =
0; начало цикла по / от 1 до 10 |
w(U)
= m(l,l)
+ /4;
w(l,2)==w(l,2)
+ /3;
=
0; начало цикла по / от 1 до 10 |
w(U)
= m(l,l)
+ /4;
w(l,2)==w(l,2)
+ /3;
в цикле no
i
от 1 до 3 в цикле по
j
от 1 до 3 если
 то в цикле по k
от
i+1
до 4 выполнять
то в цикле по k
от
i+1
до 4 выполнять


вывод на экран значений а, b, с;
начало цикла по i от 1 до 10
 I I
I I
| вывод на экран значений i, yi, у1, d
конец цикла по i;
ожидание нажатия клавиши «Enter»;
переход в графический режим 640480;
задание масштаба тх = 50 ; ту = 40;
линия от (10,460) до (630,460);
линия от (630,460) до (622,463);
линия от (630,460) до (622,457);
центровка текста по горизонтали и вертикали;
вывод буквы х в позицию (630,467);
начало цикла по i от 1 до 10
| линия от (50 + i*mx,460) до (50+i*mх,457 );
| преобразование значения i в строку s;
| вывод s в позицию (50 +i*mх, 467 );
| вывод окружности радиусом 3
|и центром (50 +i*тх, 460 – round(yt*ту))
конец цикла по i;
начало цикла по i от 50 до 499
|

|

| линия от

|
до

конец цикла по i; ожидание нажатия на любую клавишу
конец программы.
Контрольные вопросы
1. Для чего нужна аппроксимирующая функция?
2. В чем заключается метод наименьших квадратов?
3. Как получается нормальная система?
4. Каким методом можно решить нормальную систему?
5. Как графически проверить правильность расчета коэффициентов аппроксимирующей функции?
Содержание отчета.
Отчет должен содержать исходные данные, постановку задачи, сведения о методе решения, текст программы, полученные результаты и график.
ЛАБОРАТОРНАЯ РАБОТА № 6
ЗАДАЧА КОШИ ДЛЯ ОБЫКНОВЕННОГО
ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ
Задание. Найти частное решение дифференциального
Уравнения
 ,
удовлетворяющее условию
,
удовлетворяющее условию
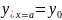 на отрезке [a,b]
с точностью
;
построить график функции y(x)
на отрезке [a,b].
на отрезке [a,b]
с точностью
;
построить график функции y(x)
на отрезке [a,b].
Краткое описание методов
В этой лабораторной работе решение
дифференциального уравнения проводится
одновременно тремя методами:
методом
Эйлера, модифицированным методом Эйлера
и
методом Рунге-Кутта.
Вычисления будут закончены, когда
требуемая точность будет достигнута
по одному из трех методов в конце отрезка
x=b.
Численное решение задачи состоит в
построении таблицы приближенных значений
 решения уравнения
в точках
решения уравнения
в точках
 Чаще всего
Чаще всего
 где n- число разбиений,
где n- число разбиений,
 -
шаг. В методе Эйлера величины
вычисляются по формуле
-
шаг. В методе Эйлера величины
вычисляются по формуле


Этот метод относится к группе одношаговых
методов, в которых для расчета точки
 требуется информация только о последней
вычисленной точке
требуется информация только о последней
вычисленной точке .
Геометрическая интерпретация одного
шага метода Эйлера заключается в
аппроксимации решения на отрезке
касательной
.
Геометрическая интерпретация одного
шага метода Эйлера заключается в
аппроксимации решения на отрезке
касательной
 ,
проведенной в точке
к интегральной кривой, проходящей через
эту точку (рис.7). А так как
,
проведенной в точке
к интегральной кривой, проходящей через
эту точку (рис.7). А так как
 .
Таким образом,
после выполнения N
шагов неизвестная интегральная кривая
заменяется ломаной линией (.ломаной
Эйлера),
для которой угловой коэффициент
очередного
i
-го звена
.
Таким образом,
после выполнения N
шагов неизвестная интегральная кривая
заменяется ломаной линией (.ломаной
Эйлера),
для которой угловой коэффициент
очередного
i
-го звена
 Для оценки погрешности метода на одном
шаге точное решение раскладывается в
ряд Тейлора в окрестности узла
Для оценки погрешности метода на одном
шаге точное решение раскладывается в
ряд Тейлора в окрестности узла
 .
Сравнение
этого разложения с формулой (6.1) показывает,
что они согласуются до членов первого
порядка по h. Поэтому метод
Эйлера - метод первого порядка точности.
В
модифицированном
методе Эйлера вычисления
разбивают на два этапа. На первом этапе
(этапе
прогноза)
в соответствии с методом Эйлера вычисляют
грубое приближение
.
Сравнение
этого разложения с формулой (6.1) показывает,
что они согласуются до членов первого
порядка по h. Поэтому метод
Эйлера - метод первого порядка точности.
В
модифицированном
методе Эйлера вычисления
разбивают на два этапа. На первом этапе
(этапе
прогноза)
в соответствии с методом Эйлера вычисляют
грубое приближение
 .
В точке
определяют угловой коэффициент
.
В точке
определяют угловой коэффициент
 .
На втором этапе вычисляют усредненное
значение углового коэффициента
.
На втором этапе вычисляют усредненное
значение углового коэффициента
 .
Уточненное значение находят по формуле
.
Уточненное значение находят по формуле
 .
Этот метод имеет второй порядок точности.
Методом Рунге-Кутта обычно называют
одношаговый четырехэтапный метод
четвертого порядка точности:
.
Этот метод имеет второй порядок точности.
Методом Рунге-Кутта обычно называют
одношаговый четырехэтапный метод
четвертого порядка точности:



Этот метод весьма прост и, как показывает практика, довольно эффективен в обычных расчетах, когда отрезок [a,b] не очень велик и нужна сравнительно невысокая точность.
Варианты исходных данных
Варианты |
Уравнения |
a |
b |
|
1, 13 |
|
1,9 |
2,9 |
2,6 |
2, 14 |
|
1.6 |
2,6 |
0,8 |
3, 15 |
|
0,6 |
1,6 |
0,6 |
4, 16 |
|
0,5 |
1,5 |
5,3 |
5, 17 |
|
1,7 |
2,7 |
2,2 |
6, 18 |
|
1,4 |
2,4 |
2,5 |
7, 19 |
|
1,4 |
2,4 |
2,5 |
8, 20 |
|
0,8 |
1,8 |
1,4 |
9, 21 |
|
1,2 |
2,2 |
2,1 |
10, 22 |
|
2,1 |
3,1 |
2,5 |
11, 23 |
|
1,8 |
2,8 |
2,6 |
12, 24 |
|
1,3 |
2,3 |
3,1 |
Схема алгоритма метода



















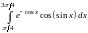


























 полученные экспериментально
полученные экспериментально