ФГБОУ ВПО «Воронежский государственный

технический университет»

Кафедра высшей математики

и физико-математического моделирования

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

для организации самостоятельной работы

по изучению раздела «Производная»

курса «Математический анализ»

для студентов направления подготовки

бакалавров 080100 «Экономика»

очной формы обучения

Воронеж 2014

Составители: канд. физ.-мат. наук Е.Г. Глушко,

канд. физ.-мат. наук Е.И. Максимова

УДК 517.9

Методические указания для организации самостоятельной работы по изучению раздела «Производная» курса «Математический анализ» для студентов направления подготовки бакалавров 080100 «Экономика» очной формы обучения / ФГБОУ ВПО «Воронежский государственный технический университет»; сост. Е.Г. Глушко, Е.И. Максимова. Воронеж, 2014. 41 с.

В методических указаниях содержатся основные теоретические положения по дифференциальному исчислению функции одной переменной, изложение теоретического материала иллюстрируется большим количеством примеров и задач, приводятся задачи и упражнения для самостоятельной работы.

Методические указания предназначены для организации самостоятельного изучения студентами первого курса раздела «Производная» по курсу математического анализа.

Методические указания подготовлены на магнитном носителе в текстовом редакторе MS Word 2007 и содержатся в файле «DERIV1. doc».

Ил. 1. Библиогр.: 6 назв.

Рецензент канд. физ.-мат. наук, доц. Н.А. Борщ

Ответственный за выпуск зав. кафедрой

д-р физ.-мат. наук, проф. И.Л. Батаронов

Издается по решению редакционно-издательского совета

Воронежского государственного технического университета

ФГБОУ ВПО «Воронежский государственный

технический университет», 2014

ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИИ

ОДНОЙ ПЕРЕМЕННОЙ

1. Производная. Правила дифференцирования

Пусть функция y = f(x) определена в некоторой окрестности точки x₀. Придадим значению переменной x в точке x₀ приращение x, при этом f(x) получит приращение f = f(x₀ + x) – f(x₀).

Определение. Если существует конечный предел

,

то он называется производной функции f(x) в точке x₀ и обозначается .

Общеприняты и другие обозначения производной функции y = f(x): , ; если же y зависит от значения переменной t (времени), то часто вместо пишут . Если вышеуказанный предел существует в каждой точке интервала (a, b), то становится функцией, определённой на (a, b).

Пример 1. Используя определение производной, найти производную функции y = sin (2x + 1).

Решение. Придадим значению переменной x приращение

 x , тогда функция y получит приращение

y = f(x +  x) – f(x) = sin (2(x +  x) + 1) – sin (2 x + 1)) =

= 2 sin x cos(2x + x + 1).

Отсюда находим

Таким образом, .

Процесс нахождения производной часто называют дифференцированием.

2. Таблица производных

(Здесь и ниже C – постоянная величина.)

; ;

; ;

; ;

; ;

; .

3. Правила дифференцирования

Если функции f(x) и g(x) имеют производные и , то функции , , , также имеют производные (последняя – при условии ), и при этом

1. ;

2. ;

3. ;

4. .

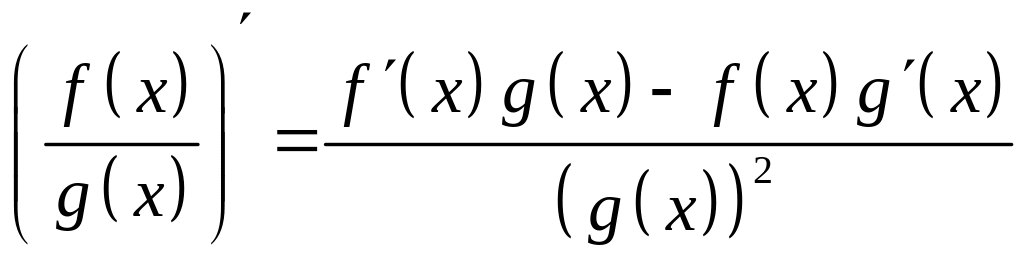Теорема 1 (о производной сложной функции). Пусть функции , определённая в окрестности точки x₀ , и z = g (y), определённая в окрестности точки y₀ = f (x₀) , обладают тем свойством, что существуют производные и . Тогда функция u (x) = g (f (x)) имеет производную в точке x₀ и при этом

.

Пример 2. Найти производные функций:

а) ; б) ;

в) ; г) .

Решение. а), б) Применяя правила дифференцирования, находим

= ;

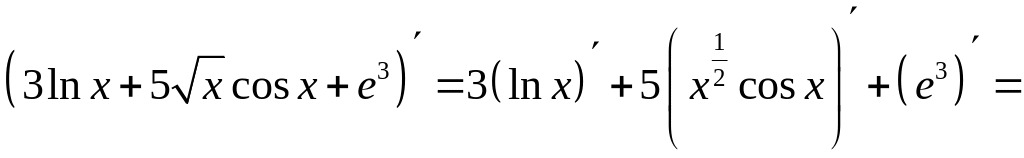
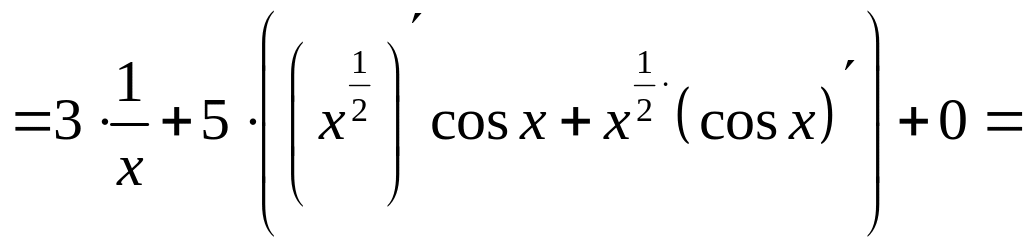
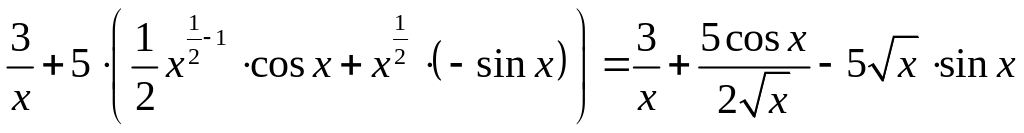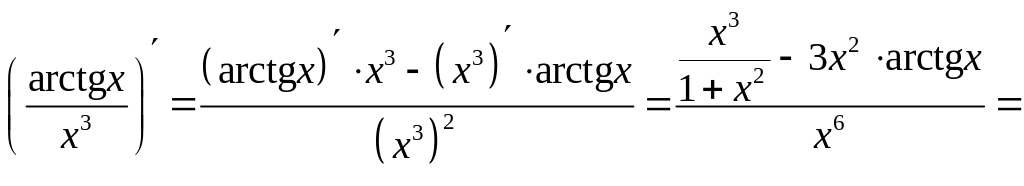
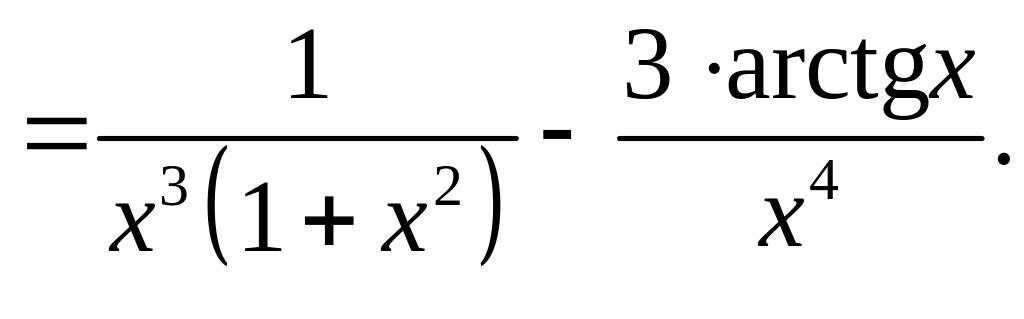
в), г) Применяя теорему о дифференцировании сложной функции, находим

= ;

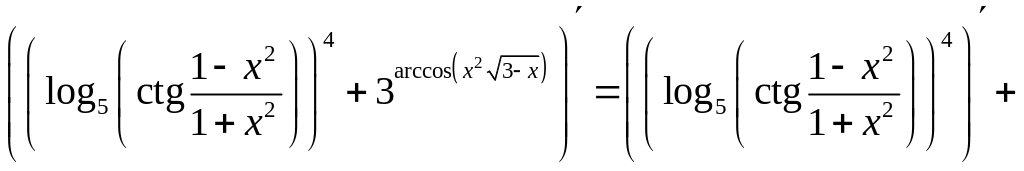
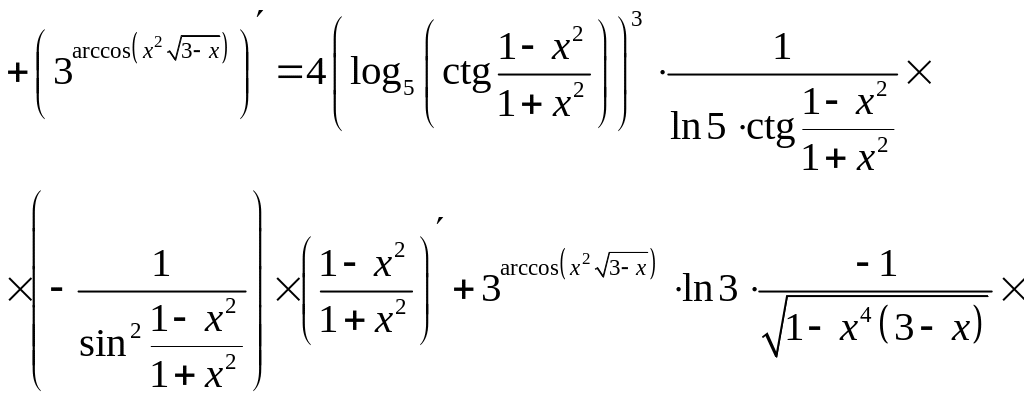
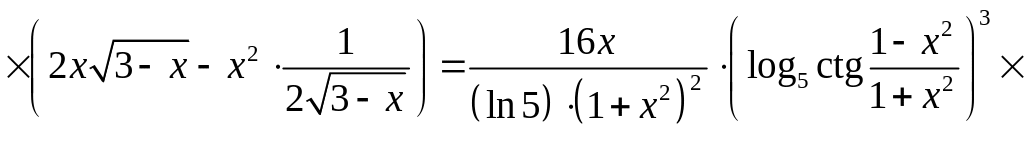
Пример 3. Показать, что функция удовлетворяет уравнению .

Решение. Найдём производную функции

.

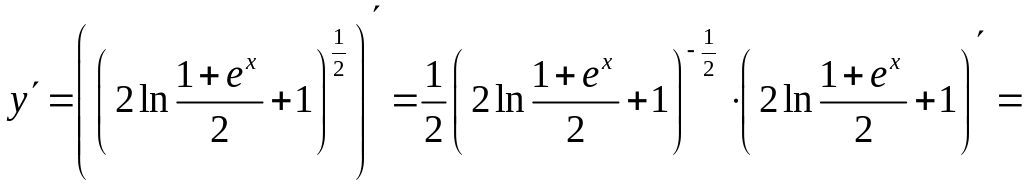
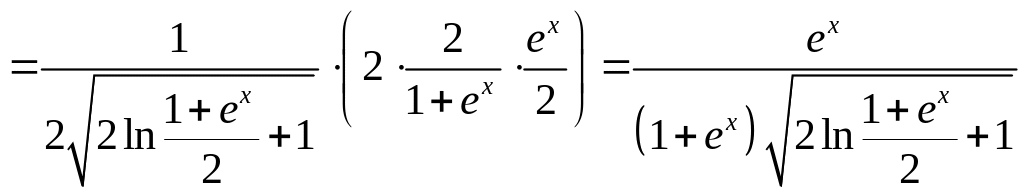Подставив это выражение в уравнение, получим

,

или .Это и доказывает, что наша функция удовлетворяет уравнению.

Для дифференцирования степенно-показательной (вида ) и некоторых других функций удобно пользоваться так называемым логарифмическим дифференцированием.

Пример 4. Найти производные функций:

а) ; б) .

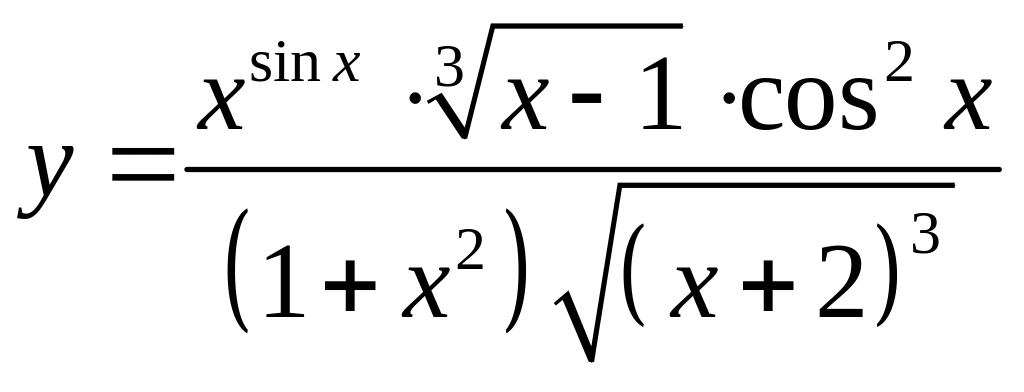Решение. а) Предварительно прологарифмируем обе части равенства , имеем . Продифференцируем обе части последнего равенства, считая ln y сложной функцией от x : ;

отсюда находим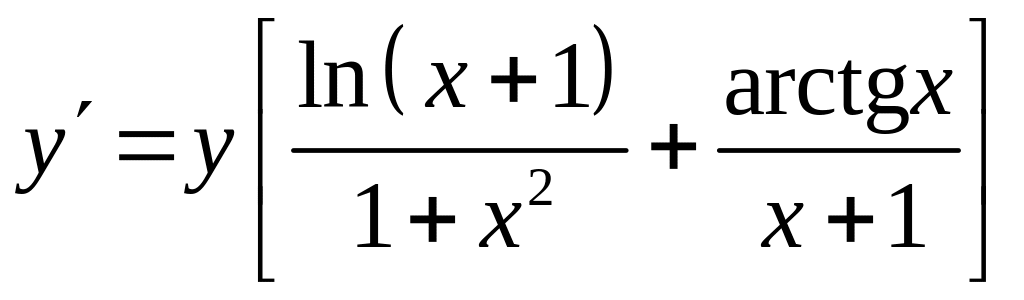 . Подставив , наконец получим

.

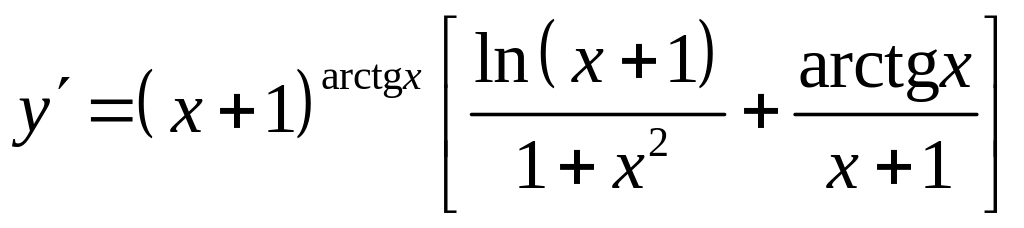б) Действуя так же, находим:

;

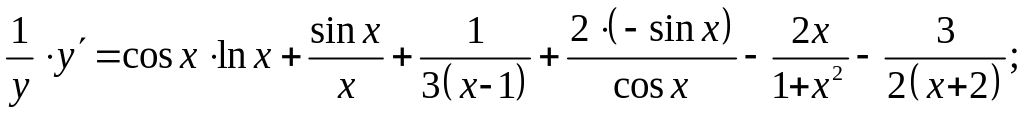
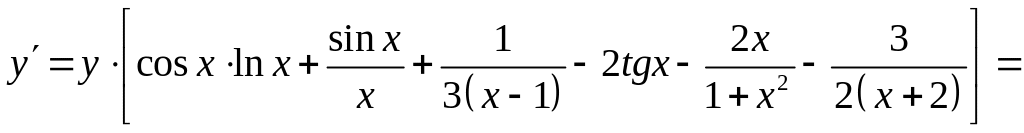
4. Производные высших порядков

Производную от производной называют второй производной от функции f(x) и обозначают . Производную от называют третьей производной функции f(x) и обозначают . Таким образом,

, , ... , , . . .

Общепринятыми являются и другие обозначения производной n-го порядка функции y = f(x): или . Если функция f(x) зависит от переменного t (времени), то вторую и третью производные иногда обозначают .

Пример 5. Найти , если y = ln(sinx) .

Решение. ;

.
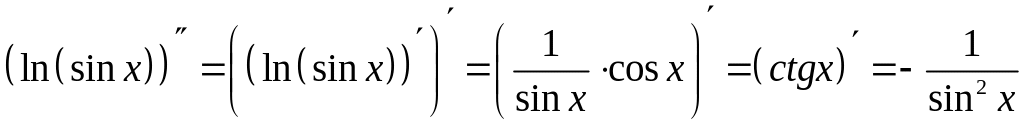
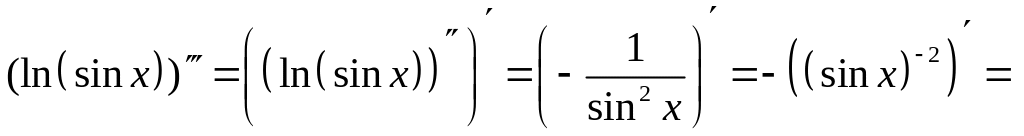