ФГ БОУВПО
«Воронежский государственный технический университет»
Кафедра автоматизированных и вычислительных систем
***-2011
Методические указания
по выполнению лабораторных работ по дисциплине "Дискретная математика"
для студентов специальности 230101
«Вычислительные машины, комплексы, системы и сети»
очной формы обучения
Часть 1
Воронеж 2011
Составители: д-р техн. наук Т.М. Леденева,
канд. техн. наук Т.Н. Недикова,
канд. физ.-мат. наук С.Ю. Балашева
УДК 681.3.06
Методические указания по выполнению лабораторных работ по дисциплине "Дискретная математика" для студентов специальности 230101 «Вычислительные машины, комплексы, системы и сети» очной формы обучения. Ч. 1 / ФГ БОУВПО «Воронежский государственный технический университет»; сост. Т.М. Леденева, Т.Н. Недикова, С.Ю. Балашева. Воронеж, 2011. 42 с.
В методических указаниях приводятся ключевые слова, примеры решения задач и задачи для самостоятельного решения по темам «Множества. Отношения. Комбинаторика».
Предназначены для студентов специальности 230101 по дисциплине "Дискретная математика".
Методические указания подготовлены в электронном виде в текстовом редакторе MS Word XP и содержатся в файле ДМ_очн_1.doc.
Ил. 2. Библиогр.: 6 назв.
Рецензент д-р техн. наук, доц. Т.В.Азарнова
Ответственный за выпуск зав. кафедрой д-р техн. наук, проф. С.Л. Подвальный
Издается по решению редакционно-издательского совета Воронежского государственного технического университета
ФГ БОУВПО "Воронежский государственный технический университет", 2011
Содержание
Введение……………………………………………………... |
2 |
Операции над множествами и их свойства………………... |
2 |
Операции над отношениями………………………………... |
12 |
Основные типы отношений………………………………… |
18 |
Элементы комбинаторики…………………………………. |
28 |
Библиографический список………………………………… |
41 |
|
|
|
|
Введение
Выполнение данных лабораторных работ позволяет лучше усвоить теорию, базовые понятия дисциплины, прочувствовать связи между ними и получить практические навыки работы с объектами, являющимися предметом изучения дискретной математики, а также отработать приемы решения основных типов задач по следующим разделам: множества, отношения, комбинаторика.
Операции над множествами и их свойства
Ключевые слова: множество, подмножество, булеан; отношения включения и равенства множеств; операции над множествами и их свойства; покрытие и разбиение.
Задача 1.1. Докажите, что
.
Решение.
Чтобы доказать равенство
двух множеств
и
,
нужно показать истинность включений
и
.
Докажем, что
.
Для этого выберем произвольный элемент
из множества
и покажем, что он принадлежит множеству
.
Итак, пусть
,
тогда
и
.
Если
,
то
,
и
.
Если
,
то
,
а значит,
.
Таким образом,
.
Теперь докажем другое включение
.
Пусть
.
Если
,
то
и
.
Отсюда следует, что
и
,
т.е.
.
Если
,
то
и
.
Отсюда следует, что
и
,
т.е.
.
Итак,
.
Таким образом, получили, что
и
,
а это значит, что эти два множества
равны.
Решение подобных задач можно оформлять в более формализованном виде, используя скобки { для системы высказываний, объединенных союзом «и», [ - для системы высказываний, объединенных союзом «или».
Задача
1.2. Докажите следующее утверждение: если
,
то
.
Решение.
Чтобы доказать
,
выберем произвольный элемент
и покажем, что
.
Итак,
Таким образом, , что и требовалось доказать.
Задача
1.3. Докажите, что
.
Решение. Используя свойства операций над множествами, покажем, что правую часть выражения с помощью равносильных преобразований можно свести к левой.
Задача
1.4. Упростите выражение
.
Решение. Упростим выражение с помощью равносильных преобразований
Задача 1.5. Пусть заданы множества
,
.
Убедитесь,
что
.
Решение. Прежде всего, заметим, что универсальным множеством здесь является
,
тогда
.
Найдем
,
,
,
,
откуда следует, что .
Задача
1.6. Существуют ли множества
,
удовлетворяющие условиям
?
Решение.
Изобразим множества
в виде прямоугольников, расположенных
на плоскости в общем положении, и поставим
в соответствие каждой полученной области
некоторый символ. Например, символ 4
обозначает совокупность всех элементов,
попавших во множества
и
,
но не попавших во множество
.
Теперь составим множества
и универсальное множество
,
так что каждому множеству будет
соответствовать совокупность определенных
символов (рис. 1.). Получим
.
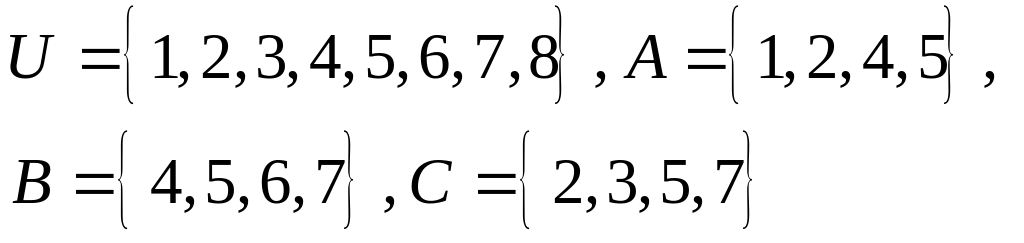Рис. 1.
Изменим
множества
так, чтобы выполнились условия нашего
задания. Из того, что
,
следует, что множество
не должно содержать элементов, т.е. из
удаляем
и
.
Чтобы выполнилось условие
,
нужно удалить элементы списков
.
Тогда получится, что множества
примут вид:
.
Заметим,
что для этих множеств
.
Если
под символами
понимать соответствующие числа, то мы
получим конкретный пример множеств
,
для которых выполнены все условия
заданного набора требований.
Задача 1.7. Выясните взаимное расположение множеств
,
если - произвольные подмножества универсального множества .
Решение. Возьмем множества , находящиеся в общем положении. Из рис.222 следует, что
.
В данном случае, как и при решении предыдущей задачи, цифры обозначают соответствующие совокупности элементов множеств. Тогда
,
,
тогда
.
Заметим,
что выполняются включения
и
для любых множеств
.
Таким образом, множества
и
могут находиться в общем положении.
Задача
1.8. Докажите, что для любых множеств
из условия
следует включение
.
Решение. Возьмем множества , находящиеся в общем положении, тогда на основе рис. определим
.
В
данном случае, как и при решении предыдущей
задачи, цифры обозначают соответствующие
совокупности переменных. Тогда
и из включения
следует, что список
пуст,
.
Рассмотрим
и
.
,
.
Так как
,
то включение
имеет место в предположении, что
.
Задачи для самостоятельного решения
1. Перечислите элементы множеств
а)
;
б)
;
в)
;
г)
;
д)
.
2. Опишите следующие множества с помощью характеристического свойства:
а)
;
б)
;
в)
;
г)
;
д)
.
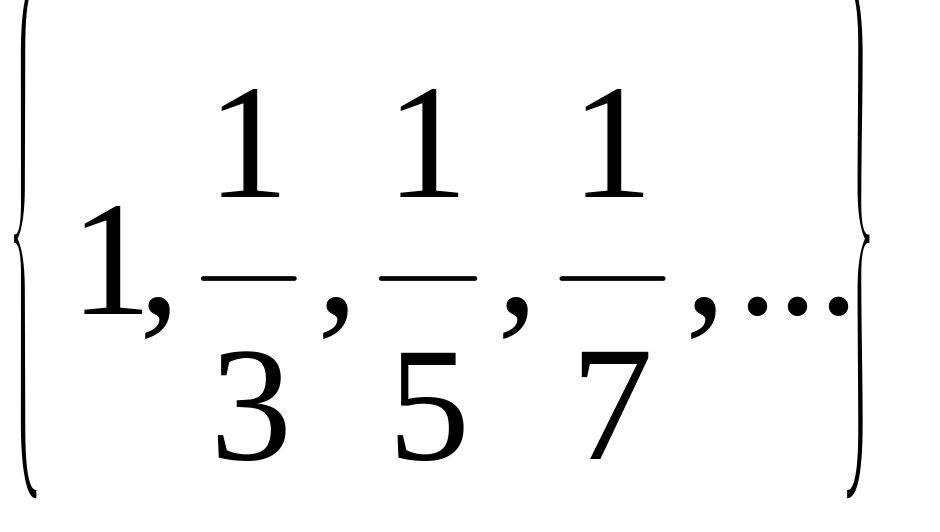3. Установите истинность или ложность каждого из следующих утверждений:
а)
( - произвольное множество);
б)
,
в)
.
4.
В качестве универсального множества
данной задачи зафиксируем
.
Пусть
,
,
.
Найдите элементы следующих множеств:
,
,
,
,
,
.
5. Рассмотрим следующие подмножества целых чисел
,
,
.
Используя операции на множествах, выразите следующие подмножества через :
а)
;
б)
;
в)
.
6.
Наследником множества
называется множество
.
Определите наследников следующих
множеств
а)
,
б)
,
в)
.
7.
Множество
всех подмножеств множества
называется булеаном (или показательным
множеством) Докажите, что
а)
;
б)
;
в)
покажите на примере, что
не всегда совпадает с
.
8. Выразите операции
а)
через
;
б)
через
;
в)
через
.
9. Доказать, что нельзя выразить
а)
через
и
;
б) через и .
10.
Докажите, что если
,
то справедливы следующие соотношения
для любых множеств
и
:
а)
;
б)
в)
;
г)
;
д)
.
11.
Докажите, что если
,
то
и
.
12.
Докажите, что если
,
то
.
13.
Докажите, что для любых множеств
,
таких что
,
справедливо
.
14.
Докажите, что для произвольных множеств
справедливы следующие соотношения:
а)
;
б)
;
в)
;
г)
.
15.
Пусть
и
.
Доказать, что в этом случае
.
16. Докажите
а)
,
б)
,
в)
,
г)
,
д)
.
17. Докажите:
а)
если
,
то
и
,
б)
если
,
то
и
,
в)
если
,
то
,
г)
если
,
то
.
18.
Для универсального множества
,
множества
,
заданного списком, и для
,
являющегося множеством корней уравнения
,
найдите множества
,
если
а)
,
,
б)
,
,
в)
,
,
г)
,
.
19. Постройте диаграммы Венна для следующих множеств
а)
,
б)
,
в)
,
г)
.
20.
С помощью диаграмм Венна докажите, что
.
Покажите на примере, что множество
не обязательно совпадает с множеством
.
21.
Определим операцию
по формуле
.
Изобразите на диаграмме Венна множество
.
С помощью законов алгебры множеств
докажите тождества
а)
,
б)
,
в)
.
23. Существуют ли множества , удовлетворяющие заданному набору условий?
а)
;
б)
;
в)
;
г)
;
д)
;
е)
.
24.
Выясните взаимное расположение множеств
,
если
- произвольные подмножества некоторого
универсального множества
:
|
|
|
|
1 |
|
|
|
2 |
|
|
|
3 |
|
|
|
4 |
|
|
|
5 |
|
|
|
6 |
|
|
|
25.
Проверьте, что для любых множеств
справедливо
включение
,
если
и
заданы в таблице:
|
|
|
1 |
|
|
2 |
|
|
3 |
|
|
4 |
|
|
5 |
|
|
6 |
|
|
