
Учебное пособие 1888
.pdf
Так как |
f (x) |
3x2 0.4x 0.2 |
и |
при x3 |
x |
1.5 имеем |
|
f (x) |
3 1.1982 |
0.4 1.5 |
0.2 |
3 1.43 0.8 |
3.49 , |
то можно |
|
принять |
|
|
|
|
|
|
|
|
0 |
x3 |
0.0072 |
0.002 . |
|
|
|
|
|
|
|
||||
|
3.49 |
|
|
||||
|
|
|
|
|
|
|
|
Таким образом, |
1.198 |
0.002 |
, |
где 0 |
1. |
|
|
4.4.МЕТОД НЬЮТОНА
Если известно хорошее начальное приближение решения уравнения (4.1), то эффективным методом повышения точности является метод Ньютона (метод касательных). Метод состоит в построении итерационной последовательности
|
|
|
|
xn 1 |
xn |
|
|
f (xn ) |
. |
|
|
|
(4.8) |
|
|
|
|
|
|
f (xn ) |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Достаточные условия сходимости этого метода содержатся в |
|||||||||||||
следующей теореме. |
|
|
|
|
|
|
|
|
|
|
||||
|
Теорема. Пусть функция |
f (x) |
определена и дважды |
диффе- |
||||||||||
ренцируема на отрезке a, b , |
причем f (a) |
f (b) |
0 , а производ- |
|||||||||||
ные |
f (x), f |
(x) |
сохраняют знак на отрезке |
a, b . Тогда, исходя |
||||||||||
из начального приближения |
x0 |
|
a, b , удовлетворяющего нера- |
|||||||||||
венству f (x0 ) |
f (x0 ) |
0 , |
можно построить последователь- |
|||||||||||
ность xn 1 |
xn |
|
f (xn ) |
, |
n |
0, 1, 2, ..., |
сходящуюся к един- |
|||||||
|
f (xn ) |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ственному на |
a, b решению |
|
|
уравнения f (x) 0 . |
|
|||||||||
|
Геометрически метод Ньютона эквивалентен замене не- |
|||||||||||||
большой дуги кривой y |
f (x) касательной, проведенной в некото- |
|||||||||||||
рой точке кривой (рис. 9). |
|
|
|
|
|
|
|
|
|
|
||||
|
Выберем, например, x0 |
b , для которого |
f (x0 ) f (x0 ) 0 . |
|||||||||||
Проведем касательную к кривой |
y |
f (x) в точке B0 (x0 , f (x0 )) . |
||||||||||||
В качестве первого приближения x1 |
корня |
возьмем абсциссу точ- |
||||||||||||
ки |
пересечения |
этой касательной |
с осью |
OX . |
Через |
точку |
||||||||
71
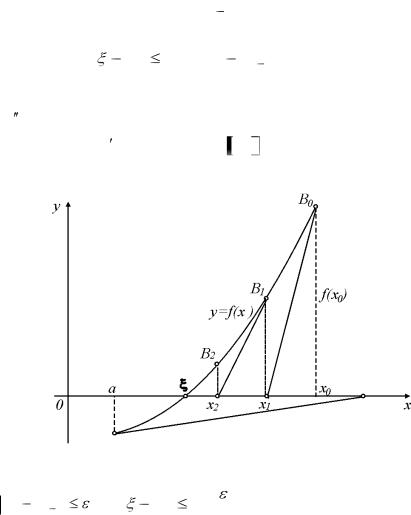
B1(x1, f (x1)) снова проведем касательную, абсцисса точки пересечения которой даст второе приближение x2 корня 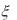 и т.д. (рис. 9).
и т.д. (рис. 9).
Для оценки погрешности n приближения корня можно воспользоваться неравенством
|
|
|
|
xn |
|
|
M 2 |
|
xn |
xn 1 |
|
2 |
, |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
2m1 |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где M 2 - наибольшее значение |
модуля второй производной |
|||||||||||||
|
f (x) |
на отрезке |
a, b |
; |
m1 - наименьшее значение модуля первой |
||||||||||
|
на отрезке a, b . Таким образом, |
|
|||||||||||||
производной |
f (x) |
если |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 9 |
||
|
|
|
|
|
|
|
M |
|
2 |
|
xn xn 1 |
|
, то |
|
xn |
|
|
2 |
|
. Последнее соотношение оз- |
|
|
|
|
|
|||||||
|
|
|
|
2m1 |
|
|||||
|
|
|
|
|
|
|
|
|
||
начает, что при хорошем начальном приближении корня после каждой итерации число верных десятичных знаков в очередном приближении удваивается, т.е. процесс сходится очень быстро.
72

4.5. КОМБИНИРОВАННЫЙ МЕТОД
Иногда для нахождения приближенного значения корня целесообразно использовать смешанные методы. Рассмотрим этот прием на примере метода хорд и касательных. Соединяя эти методы, получаем метод, на каждом этапе которого находим значения по не-
достатку и значения по избытку точного корня |
|
уравнения (4.1). |
||||||||
Пусть |
f (x) |
0 и |
f (x) 0 |
при |
a |
|
x b . Полагаем |
|||
x0 a , |
x0 |
b получим |
|
|
|
|
|
|
|
|
|
x |
a |
(b a) f (a) |
, |
x |
b |
|
f (b) |
. |
|
|
|
|
|
|||||||
|
1 |
|
f (b) |
f (a) |
1 |
|
|
f (b) |
||
|
|
|
|
|
|
|||||
Значения |
x1 |
и x1 , лежат по разные стороны от искомого корня |
||||||||
(так как |
f (x1 ) и |
f (x1 ) |
имеют разные знаки). Далее на x1, x1 |
|||||||
применим снова метод хорд и метод касательных. В результате по-
лучаем два числа |
x2 |
и |
x2 |
еще более близких к значению корня. |
||||||||||||||||
Продолжая |
таким образом до тех пор, пока разность между |
най- |
||||||||||||||||||
денными приближенными значениями не станет меньше, |
чем тре- |
|||||||||||||||||||
буемая точность, получим формулы |
|
|
|
|
|
|
|
|
||||||||||||
|
xn |
1 |
xn |
|
(xn |
|
xn ) f (xn ) |
, |
(n |
0, 1, 2, ...) . |
|
|
|
|||||||
|
|
|
f (xn ) |
|
f (xn ) |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
xn |
1 |
xn |
|
f (xn ) |
|
, |
(n |
|
0, 1, 2, ...) . |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
f (xn ) |
|
|
|
|
|
|
|
|
||||
|
Пример. Вычислить с точностью до |
0.0005 положительный |
||||||||||||||||||
корень уравнения x5 |
x |
0.2 |
|
0 . |
|
|
|
|
|
|
|
|
||||||||
|
Решение. |
Так как |
|
f (1) |
0 и |
f (1.1) |
0 , то корень |
лежит |
||||||||||||
в интервале (1; 1.1), т.е. |
1 |
|
1.1. |
Имеем: f (x) |
|
5x4 |
1 |
|||||||||||||
и |
f (x) |
20x3 . В |
выбранном нами интервале |
f |
(x) |
|
0 ; |
|||||||||||||
f |
(x) 0 , |
т.е. |
знаки производных сохраняются. |
|
|
|
|
|||||||||||||
Применим |
комбинированный |
метод, |
полагая |
x0 |
1 |
и |
||||||||||||||
x0 |
1.1 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Так как |
f (x0 ) |
|
f (1) |
|
|
0.2 ; |
|
f (x0 ) |
f (1.1) |
0.3105; |
|||||||||
73

f (x0 ) |
f |
(1.1) |
6.3205, |
то формулы (4.6) и (4.8) |
дают: |
|||||||||||
|
x |
1 |
0.1 0.2 |
|
1.039 ; |
x |
1.1 |
0.31051 |
|
1.051. |
||||||
|
|
|
|
|
|
|
|
|
||||||||
|
1 |
|
0.51051 |
|
|
|
1 |
|
6.3205 |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
||||||
|
Ввиду того, что x1 |
x1 |
0.012, то точность недостаточ- |
|||||||||||||
ная. |
Находим следующую пару приближений: |
|
||||||||||||||
x2 |
1.039 |
|
0.012 0.0282 |
1.04469, x2 |
1.051 |
0.313 |
|
1.04487. |
||||||||
|
|
|
|
|
|
|
|
|
|
|||||||
|
0.0595 |
|
|
|
5.1005 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||
Здесь x2 |
|
x2 |
0.00018, |
т.е. нужная степень точности достиг- |
||||||||||||
нута. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4.6. МЕТОД ИТЕРАЦИИ
Одним из наиболее важных способов численного решения уравнений является метод итераций (метод последовательных приближений), который заключается в следующем.
Пусть дано уравнение (4.1) и требуется определить его действительные корни. Заменим это уравнение равносильным уравнением вида:
|
|
x |
(x) . |
|
|
(4.9) |
|
|
Выберем каким-либо способом начальное приближение |
x0 |
|||||
искомого |
корня |
|
|
и |
вычислим |
||
x1 |
(x0 ), x2 |
(x1), ..., |
xn |
(xn |
1), .. . Получим последо- |
||
вательность чисел |
x0 , x1, ..., |
xn , ... |
. Если эта последовательность |
||||
– сходящаяся, т.е. существует предел, |
|
lim xn , то число |
яв- |
||||
|
|
|
|
|
n |
|
|
ляется корнем уравнения (4.1). Действительно, переходя к пределу в
равенстве |
xn |
(xn |
1) к |
пределу |
при n |
, |
получим |
( ) , |
то есть |
- |
корень уравнения |
(4.1). При достаточно |
|||
большом |
n xn мало отличается от , следовательно, |
xn |
является |
||||
приближенным значением корня уравнения (4.1). |
|
||
|
Геометрически способ итерации можно показать следующим |
||
образом. На плоскости XOY строятся графики функций |
y x и |
||
y |
(x) . Абсцисса точки пересечения |
этих графиков |
является |
действительным корнем. Взяв в качестве |
начальной произвольную |
||
74

точку x0 a, b , строим ломаную линию. Абсциссы вершин этой ломаной представляют собой последовательные приближения корня
. Из рисунков видно, что если |
(x) |
0 |
на отрезке a, b , то |
|
последовательные приближения xn |
(xn |
1) |
колеблются около |
|
корня |
(ломаная называется “спираль”) (рис. 10), |
|||
Рис. 10
если же производная (x) положительна, то последовательные
приближения сходятся к корню монотонно (ломаная называется “лестница” рис. 11).
Можно указать случаи, когда процесс итерации может быть расходящимся. Это происходит в том случае, когда (x) 1 .
Достаточные условия сходимости последовательности итераций содержатся в следующей теореме.
75
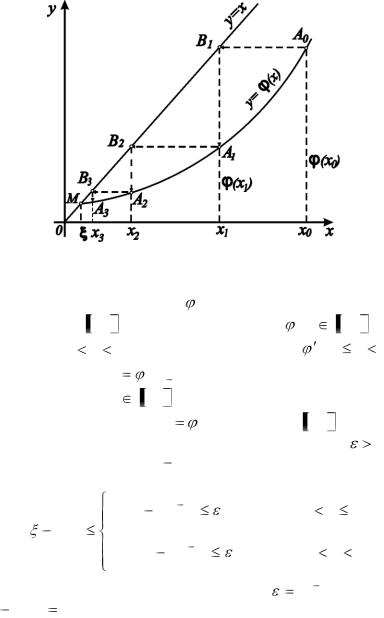
Рис. 11
Теорема. Пусть функция (x) определена и дифференцируе-
ма на отрезке |
a, b , причем все ее значения |
(x) |
a,b . Тогда, |
|||||||||||||||||||
если для всех a |
x |
|
b выполняется неравенство |
|
|
|
|
(x) |
|
|
q |
1, то |
||||||||||
|
|
|
|
|
|
|
||||||||||||||||
процесс итерации |
xn |
(xn 1 ) |
|
сходится независимо от |
началь- |
|||||||||||||||||
ного приближения |
x0 |
a, b . |
Предельное значение является един- |
|||||||||||||||||||
ственным корнем уравнения x |
|
|
(x) на отрезке |
|
a, b . |
|
|
|
|
|||||||||||||
При нахождении корня (4.1) с заданной точностью |
|
|
|
0 или |
||||||||||||||||||
при оценке погрешности |
k |
го приближения |
можно воспользо- |
|||||||||||||||||||
ваться следующей формулой |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
x(k ) |
|
x(k 1) |
|
|
|
при |
0 |
|
q |
|
1 |
|
; |
|||||
|
|
|
|
|
|
|
|
|
||||||||||||||
|
x(k ) |
|
|
|
|
|
|
2 |
|
|||||||||||||
|
|
|
|
x(k ) |
x(k |
|
|
|
|
1 |
|
|
|
|
|
|||||||
|
|
|
|
1) |
|
|
|
|
|
|
||||||||||||
|
|
|
10 |
|
при |
|
q |
1. |
||||||||||||||
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
2 |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Пример. |
Решить |
|
с |
точностью |
|
10 2 |
|
уравнение |
||||||||||||||
2x cos x 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
76

Решение. Для отделения корней представим это уравнение в |
|||||||
виде x |
|
1 |
cos x. Построив графики функций y |
x и y |
1 |
cos x , |
|
2 |
2 |
||||||
|
|
|
|
||||
видим, |
что корень этого уравнения содержится |
внутри |
отрезка |
||||
0, |
|
|
(рис.12). f (x) 2x |
cosx; f (x) 2 sin x 0. Поло- |
|||
2 |
|
||||||
жим, |
x(0) |
0.5. Последовательные приближения найдем по фор- |
|||||
мулам |
x(k |
1) |
1 |
cos x(k ) |
(k 0,1,2,...) : |
||
|
|||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 12 |
|
|
x(1) |
1 |
|
cos x(0) |
1 |
|
cos0.5 0.43879128; |
||||||||
2 |
2 |
|||||||||||||
|
|
|
|
|
|
|
|
|||||||
x(2) |
|
|
1 |
cos x(1) |
|
|
1 |
cos0.43879128 |
0.45263292; |
|||||
2 |
2 |
|||||||||||||
|
|
|
|
|||||||||||
x(3) |
|
1 |
cos x(2) |
|
1 |
cos0.45263292 |
0.44964938; |
|||||||
2 |
2 |
|||||||||||||
|
|
|
|
|
|
|||||||||
77
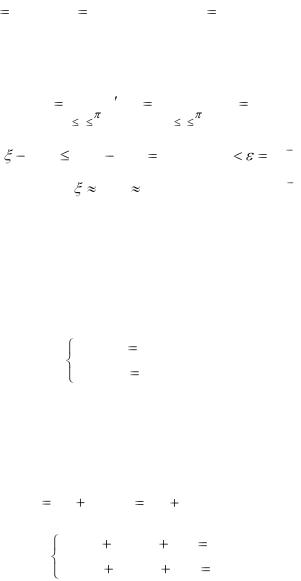
x(4) |
1 |
cos x(3) |
1 |
cos0.44964938 0.45029978. |
|
|
|||
2 |
|
2 |
|
|
Для оценки погрешности четвертого приближения воспользуемся неравенством (11.1).
|
|
|
|
|
|
|
|
1 |
|
|
|
1 |
|
||||
Так как |
q |
max |
q (x) |
|
max sin x |
, |
|||||||||||
|
2 |
2 |
|||||||||||||||
|
|
|
|
0 x |
|
|
|
|
0 x |
|
|
|
|||||
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
2 |
|
|
|
|
|
|
2 |
|
|
|
|||
|
x(4) |
|
|
x(4) x(3) |
|
0.0006504 |
|
10 3. |
|||||||||
то |
|
|
|
|
|
||||||||||||
Следовательно, |
|
|
x(4) |
|
0.450 с точностью 10 3. |
||||||||||||
4.7. МЕТОД НЬЮТОНА ДЛЯ СИСТЕМЫ ДВУХ УРАВНЕНИЙ
Рассмотренные выше способы решения уравнений могут быть перенесены на случай нелинейных систем уравнений с несколькими неизвестными. Разберем случай системы двух уравнений с двумя неизвестными.
Пусть система уравнений имеет вид:
F1 |
(x, y) 0 |
|
(4.10) |
F2 (x, y) 0,
где F1(x, y) и F2 (x, y) - непрерывно дифференцируемые функции. Пусть xn , y n - приближенные корни этой системы и будем искать поправки к этим значениям. Обозначив эти поправки соот-
ветственно через hn и |
kn , |
запишем точные значения корней x , y |
в виде: |
|
|
x xn |
hn , |
y yn kn . |
Таким образом, |
вместо системы (4.10) имеем: |
|
F1(xn |
hn , yn |
kn ) 0 |
|
|
(4.11) |
F2 (xn |
hn , yn |
kn ) 0. |
Разложим функции F1(x, y) и F2 (x, y) в ряд Тейлора, ограничиваясь линейными членами относительно hn и kn . Будем иметь
78

F1(xn , yn ) hn |
|
|
F1(xn , yn ) |
kn |
|
F1(xn , yn ) |
0 |
||||||||||||||
|
|
|
x |
|
|
|
|
|
y |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(4.12) |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F2 |
(xn , yn ) hn |
|
F2 (xn |
, yn ) |
|
kn |
|
F2 |
(xn |
, yn ) |
0. |
||||||||||
|
|
x |
|
|
|
|
|
|
y |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Если якобиан этой системы |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
F1(xn , yn ) |
|
F1(xn , yn ) |
|
|
||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||
|
J (xn , yn ) |
|
|
x |
|
|
|
|
|
|
|
y |
|
|
|
|
0 , |
||||
|
|
F2 |
(xn , yn ) |
|
F2 (xn , yn ) |
|
|||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
y |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
то из системы (4.12) получаем значения для поправок
|
1 |
|
|
F1(xn , yn ) |
||||
hn |
|
|
|
|
|
|||
|
|
|
|
|
|
|
||
J (xn , yn ) |
F2 (xn , yn ) |
|||||||
|
||||||||
|
|
|
|
|
||||
|
|
|
|
|
|
F1(xn , yn ) |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|||
kn |
1 |
|
|
x |
||||
|
|
|
|
|
F2 (xn , yn ) |
|||
|
J (xn |
, yn ) |
|
|||||
|
|
|
||||||
|
|
|
|
|
|
x |
||
|
|
|
|
|
|
|
|
|
Следовательно, можно положить:
|
F1(xn , yn ) |
|
|
|
|
y |
, |
(4.13) |
|
|
F2 (xn , yn ) |
|||
|
y |
|
|
|
|
F1(xn , yn ) |
|
|
|
|
|
|
. |
(4.14) |
F2 (xn , yn )
|
|
1 |
|
F1(xn , yn ) |
|
xn 1 |
xn |
|
|
|
|
|
|
|
|
||
J (xn , yn ) |
|
F2 |
(xn , yn ) |
||
|
|
|
|||
|
|
|
|
||
|
|
|
|
|
|
|
F1(xn , yn ) |
|
|
|
|
y |
, |
(4.15) |
|
|
F2 (xn , yn ) |
|||
|
y |
|
|
|
|
|
|
|
|
79

|
|
|
|
|
|
|
|
|
|
|
|
F1 |
(xn , yn ) |
|
|
F1(xn , yn ) |
|
||||||
yn 1 |
yn |
|
|
|
1 |
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
(4.16) |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
F2 (xn |
, yn ) |
|
|
|
|
|
|||||||
|
J (xn , yn ) |
|
|
|
F2 (xn , yn ) |
||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( n |
|
0, 1,2,...) . |
|
|
|
|
|
||||||
Начальные значения x0 , |
y0 |
определяются приближено. |
|||||||||||||||||||||
Пример. Найти действительные корни системы |
|||||||||||||||||||||||
|
|
|
F (x, y) 2x3 |
y 2 1 0 |
|
|
|
|
|||||||||||||||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
F (x, y) |
|
|
|
xy3 |
y 4 0. |
|
|
|
|
|||||||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Решение. Графическим путем найдем грубо приближенные |
|||||||||||||||||||||||
значения корней |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
x0 |
1.2 , |
|
|
|
|
y0 1.7 . |
|
|
|
|
|
|
|||||||||
Подставив в систему в (4.10) получим: |
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
F1(1.2,1.7) |
0.434 |
|
|
|
||||||||||||
|
|
|
|
|
|
|
F2 (1.2,1.7) |
0.1956. |
|
|
|
||||||||||||
Вычислим Якобиан |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
J (x, y) |
|
6x2 |
|
|
|
|
2 y |
|
, |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
y3 |
3xy2 |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|||||||
отсюда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
J |
|
3.4 |
|
|
|
97.91. |
|
|
||||||||||
|
|
|
|
|
|
8.64 |
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
4.91 |
9.4 |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
По формуле (4.13) |
вычисляем h0 |
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
h0 |
|
|
|
1 |
|
|
0.434 |
|
3.4 |
|
|
3.389 |
0.0349, |
|||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
0.1956 |
|
9.4 |
|
|
|
|
|
|
|||||||||
|
97.91 |
|
|
|
97.91 |
||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||
отсюда по формуле (4.15) находим |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
x1 |
1.2 |
0.0349 |
|
|
|
1.2349. |
|
|
||||||||||
80
