
Учебное пособие 1828
.pdf
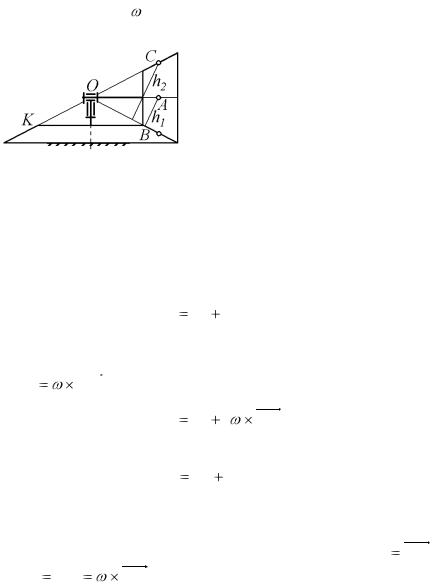
вокруг осей Oz и Oz1 (рис. 4.2). При повороте на угол dφ вокруг оси Oz любая точка тела, лежащая в плоскости zOz1 (внутри угла zOz1 ), получит элементарное, перпендикулярное к этой плоскости перемещение h1d , где h1 - расстояние точки от оси Oz . Одновременно при повороте вокруг оси Oz1 та же точка получит противоположно направленное перемещение, равное h2d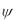 Тогда внутри угла zOz1 найдется такая точка В, для которой h1d
Тогда внутри угла zOz1 найдется такая точка В, для которой h1d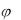 = h2d
= h2d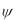 и пере-
и пере-
мещение которой равно нулю (если направление одного из вращений противоположно показанному на рис. 4.2, то такая точка лежит вне угла zOz1 ). Следовательно, элементарное перемещение, получаемое телом в результате поворотов вокруг осей Oz и Oz1 , будет таким же, как у тела, имеющего две неподвижные точки О и В, т. е. является элементарным поворотом вокруг оси ОВ, проходящей через точку О. Рассуждая таким же образом, можно установить, что элементарные повороты вокруг осей ОВ и ОК будут в свою очередь эквивалентны одному элементарному повороту вокруг некоторой, проходящей через точку О, оси ОР (рис. 4.2). Теорема доказана.
148
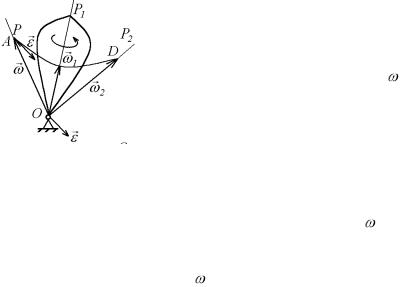
Ось ОР, элементарным поворотом вокруг которой тело перемещается из данного положения в положение соседнее, бесконечно близкое к данному, называется мгновенной осью вращения. Скорости всех точек тела, лежащих на мгновенной оси вращения, равны в данный момент времени нулю. От неподвижной оси мгновенная ось вращения отличается тем, что ее направление и в пространстве и относительно самого тела все время меняется. Переместившись поворотом вокруг оси ОР в соседнее положение, тело из этого положения в соседнее положение перемещается поворотом вокруг новой мгновенной оси вращения OP1 и т. д. Таким об-
разом, движение твердого тела вокруг неподвижной точка сводится к серии последовательных элементарных поворотов вокруг мгновенных осей вращения, проходящих через эту неподвиж-
ную точку (рис. 4.3).
Рассмотрим кинематические характеристики этого движения.
1) Угловая скорость , с которой тело совершает элементарный поворот вокруг мгновенной оси вращения, называется угловой скоростью тела в данный момент времени или мгновенной угловой скоро-
стью тела. Мгновенную угловую скорость можно изобразить соответствующим вектором , направленным вдоль оси ОР. Поскольку направление оси ОР непрерывно изменяется, модуль и направление вектора также изменяться и его конец А описывает в пространстве некоторую
149

кривую AD, являющуюся годографом вектора
(рис. 4.3).
2) Угловое ускорение тела в данный момент времени или мгновенное угловое ускорение , определяющее в данном случае изменение вектора угловой скорости , будет векторной величиной, равной
|
|
d |
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
dt |
|
||
|
Из сравнения этого выражения с равенством |
||||
|
|
|
|
|
|
v |
dr / dt следует, что |
|
угловое ускорение |
|
|
можно определять как скорость, с которой конец вектора перемешается вдоль кривой AD (см. рис. 4.3). В частности, направление совпадает с направлением касательной к кривой АD в соответствующей точке. Следовательно, при вращении тела относительно неподвижной точки, в отличие от случая вращения тела во-
круг |
неподвижной |
оси, направления векторов |
и |
различны. |
|
Векторы и |
являются основными кинема- |
|
тическими характеристиками движения тела вокруг неподвижной точки. Интегрирование этих векторов дает законы изменения угловой скорости и угла поворота тела соответственно.
Следует помнить, что конечный угол поворота тела не является вектором. Вектором может быть только бесконечно малый угол поворота тела.
§ 4.2. Скорости и ускорения точек тела
Так как при движении около неподвижной
150

точки тело имеет в каждый момент времени мгновенную ось вращения ОР, модуль скорости некоторой его точки М (рис. 4.4) будет в этот момент определяться равенством
v h , |
(4.2) |
где - угловая скорость тела, h - расстояние от точки М до мгновенной оси вращения.
|
|
|
|
|
|
|
|
|
Вектор скорости |
v |
направлен |
||||
|
перпендикулярно плоскости МОР, |
||||||
|
проходящей |
через |
|
мгновенную |
|||
|
ось ОР и точку М, в сторону |
||||||
|
вращения тела. |
|
|
|
|||
|
Формулой |
(4.2) |
|
не |
всегда |
||
|
удобно |
пользоваться |
для |
опре- |
|||
|
|
|
|
|
|
|
|
|
деления v , так как за счет пе- |
||||||
|
ремещения |
тела |
относительно |
||||
Рис. 4.4. |
вектора |
входящая в нее вели- |
|||||
чина h |
зависит от |
времени. По |
|||||
|
|||||||
этой же причине из формулы (4.2) нельзя получить выражение для ускорения точки М дифференцированием скорости этой точки, как делается при постоянном h.
Для непосредственного |
определения |
вектора |
|||
|
|
|
|
|
|
скорости v |
точки |
М рассмотрим векторное про- |
|||
|
|
|
|
|
|
изведение |
|
r , |
где r |
- вектор - |
радиус, |
проходящий из неподвижной точки О в точку М. Модуль векторного произведения
|
|
r sin |
h |
|
r |
||
|
|
|
|
совпадает с величиной скорости точки М.
|
|
|
|
|
|
Направление и размерность векторов |
|
r |
и |
|
|
|
|
|
v |
также совпадают. Следовательно, |
|
|
|
151
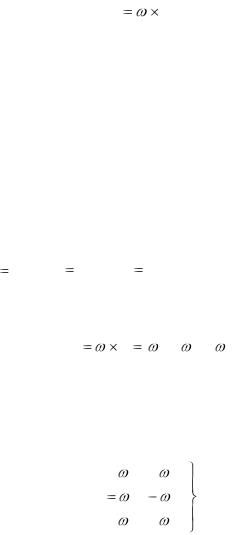
|
|
|
v |
|
r , |
(4.3)
т.е. вектор линейной скорости некоторой точки М тела равен, векторному произведению мгновенной угловой скорости тела на вектор - радиус этой точки.
Аналитически вектор v определяется по его проекциям на какие - либо оси координат, например на оси Oxyz , жестко связанные с телом
и движущиеся вместе с ним (см. рис. 4.4). Эти оси имеют то преимущество, что в них координаты х, у, z точки М будут постоянными величинами, не зависящими от времени. Учитывая,
что rx x , ry |
y , |
,rz |
|
z , |
по |
известной формуле |
|
векторной алгебры получим |
|
|
|||||
|
|
|
|
i |
j |
k |
|
|
|
||||||
|
|
|
|
|
|||
v |
|
r |
|
x |
y |
z |
. |
|
|
|
|
x |
y |
z |
|
|
|
|
|
|
|
|
|
Отсюда следуют выражения для проекций вектора скорости точки М на оси подвижной системы координат Oxyz :
vx 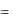 y z
y z 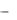 z y,
z y,
vy |
z x x z, . |
(4.4) |
vz 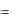 x y
x y 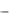 y x.
y x.
Формулы (4.3) и (4.4) называют формулами Эйлера.
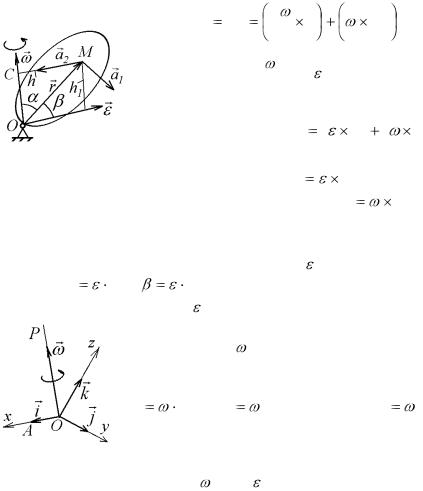
Для определения ускорения точки М продифференцируем по времени равенство (4.3). Тогда получим
152
|
|
|
|
|
|
|
|
|
|
|
|
|
d |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
dv |
|
|
|
|
|
|
|
|
|
dr |
|
|
||||||||
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
. |
|
||
|
|
|
|
|
|
|
dt |
|
|
|
|
dt |
|
|
|
|
|
dt |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
d |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dr |
|
|||||
|
|
|
|
|
Так |
как |
|
|
|
|
= |
|
, |
а |
|
|
|
|
= |
v |
||||||||
|
|
|
|
|
|
dt |
|
|
|
|
|
dt |
||||||||||||||||
|
|
|
|
то |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( |
|
|
|
|
( |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
r ) |
|
v ) |
||||||
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
(4.5) |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Рис. 4.5. |
|
|
Ускорение |
|
|
a1 |
|
|
r |
называ- |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
ется вращательным, а ускорение |
|
a2 |
|
|
|
|
v |
- |
||||||||||||||||||||
осестремительным |
ускорением |
|
|
|
точки |
М. |
|
|
Вектор |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a1 |
направлен перпендикулярно плоскости, про- |
|||||||||||||||||||||||||||
ходящей через точку M и вектор |
. Его |
|
|
модуль |
||||||||||||||||||||||||
равен |
a1 |
|
r sin |
|
h , |
где |
|
h1 |
|
|
- |
расстояние |
от |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
точки |
М |
до вектора |
|
. Вектор же |
|
a2 |
, |
перпен- |
||||||||||||||||||||
|
|
|
|
дикулярный одновременно к векто- |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
рам |
v |
|
и |
|
|
|
, |
|
|
|
|
будет |
|
направлен |
||||||||||
|
|
|
|
вдоль МС (см. рис. 4.4 и 4.5). |
||||||||||||||||||||||||
|
|
|
|
Модуль |
|
|
|
|
|
этого |
|
|
|
|
вектора |
|||||||||||||
|
|
|
|
a |
v sin90 |
|
2h , так как |
v |
|
h . |
||||||||||||||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Формулы (4.3) и (4.5) верны, |
||||||||||||||||||||||||
|
|
|
|
нечно, |
|
и |
|
при |
|
|
|
вращении |
|
|
тела |
|||||||||||||
|
Рис. 4.6. |
круг неподвижной оси, когда оба |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
вектора |
|
и |
|
|
будут |
|
направлены |
|||||||||||||||||
вдоль оси вращения. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
§ 4.3. Производные от ортов подвижных |
|||||||||||||||||||||||||||
осей |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
При |
решении |
задач |
механики в ряде |
|
|
случа- |
|||||||||||||||||||||
ев, в частности при изучении сложного движения (см. гл. 5), пользуются подвижными осями Oxyz . Когда такие оси движутся поступательно,
153

их орты i , |
|
j , k не изменяются. Если же сис- |
тема координат Oxyz (рис. 4.6) вращается,
кроме того, вокруг какой-либо оси ОР, то орты осей системы уже не будут переменными величинами, так как их направления будут зависеть от времени. В этом случае для определения производной от какого - либо заданного проек-
|
|
|
|
|
|
|
|
|
|
циями на оси Oxyz |
вектора |
u |
uxi |
uy j |
uz k надо |
||||
|
|
|
|
|
|
i , |
j |
|
|
знать |
производные |
от |
ортов |
, k . Орт i |
|||||
можно |
рассматривать |
как |
вектор |
- |
радиус- |
||||
|
|
|
|
|
|
|
|
|
|
rA |
i |
точки А, лежащей на |
оси |
Ох |
на |
расстоя- |
|||
нии единицы длины от начала О.
Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
di |
drA |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
vA . |
|
|
|
|
|
|
|
|
|
dt |
dt |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
.3), |
|
vA |
|
|
rA |
|
i , |
где |
|
- |
|||
|
|
|
поворота вокруг оси ОР. |
||||||||||||
|
|
соотношения |
получаются и |
для |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
j |
и |
k . В результате получаем |
|
||||||||||
Рис. 4.7. |
|
|
|
|
|
|
|
|
|
|
|||||
|
di |
|
i , |
|
dj |
|
j , |
dk |
k . |
(4.6) |
|||||
|
dt |
|
|
dt |
|
|
dt |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|||||
Выражения (4.6) называют формулами Пуассона.
§4.4. Общий случай движения
свободного твердого тела
Рассмотрим наиболее общий случай движения твердого тела, когда оно является свободным и может произвольно перемещаться относительно
154
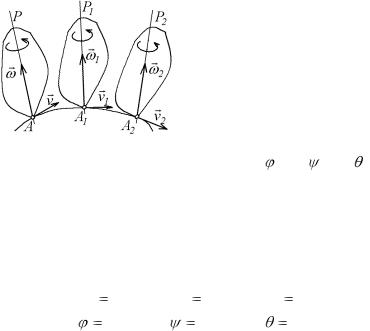
системы отсчета Ox1 y1 z1 (рис. 4.7). Составим
уравнения, определяющие закон рассматриваемого движения. Выберем произвольную точку А тела в качестве полюса и проведем через нее оси движении тела будут переме-
|
полюсом поступательно. |
Тогда |
|||
|
системе отсчета Ox1 y1 z1 |
будет |
|||
|
известно положение полю- |
||||
|
координаты x1A , y1A , z1A |
|
и по- |
||
|
тельно осей |
Axyz , определяе- |
|||
|
вращении тела относительно не- |
||||
|
подвижной |
|
точки, |
|
углами |
Рис. 4.8. |
Эйлера |
, |
, |
, |
(см. |
рис. 4.1; на рис. 4.7 углы Эйлера не показаны, чтобы не затемнять чертеж). Следовательно, уравнения движения свободного твердого тела, позволяющие найти его положение относи-
тельно системы отсчета Ox1 y1 z1 |
в любой |
момент |
|
времени, имеют вид: |
|
|
|
x1A f1( t ), y1A |
f2 ( t ), z1A |
f3 ( t ); |
|
f4 ( t ), |
f5 ( t ), |
f6 ( t ). . |
(4.7) |
Нетрудно видеть, что элементарное перемещение свободного твердого тела можно сложить из поступательного перемещения вместе с полюсом А, за счет которого полюс приходит в соседнее положение A1 , и из некоторого перемещения относительно осей Axyz , т. е. вокруг
условно неподвижной точки А. Однако последнее перемещение, согласно теореме Эйлера – Даламбера, является поворотом тела вокруг мгновенной оси вращения АР, проходящей через точку А. Следовательно, любое элементарное перемещение свободного твердого тела можно
155

представить в виде суммы элементарного по-
ступательного перемещения |
вместе |
с полюсом А |
и элементарного поворота |
вокруг |
мгновенной |
оси вращения АР, проходящей через этот полюс. Поскольку движение тела - это совокупность элементарных перемещений, движение свободного твердого тела состоит в общем случае из поступательного движения, при котором все точки тела движутся как произвольно выбранный полюс
|
|
А со скоростью vA , и из серии элементарных |
|
поворотов с угловой скоростью |
вокруг мгно- |
венных осей вращения, проходящих |
через полюс |
А (рис. 4.8). |
|
Таким будет, например, движение любого произвольно перемещающегося в воздухе тела: брошенного камня, самолета, проделывающего фигуры высшего пилотажа, артиллерийского снаряда и т. д. Наконец, аналогичной может быть движение и несвободного твердого тела при наличии соответствующих связей.
Поступательная часть движения свободного твердого тела описывается первыми тремя из уравнений (4.7), а вращение относительно полюса - последними тремя из этих уравнений.
Основными |
кинематическими |
характеристиками |
|
|
|
|
|
движения |
являются скорость |
vA |
и ускорение aA |
полюса, определяющие скорость и ускорение поступательной части движения, а также угловая скорость и угловое ускорение вращения вокруг полюса. Величины этих скоростей и ускорений в любой момент времени можно найти по уравнениям (4.7).
В частном случае движение свободного тела может быть плоскопараллельным (глава 3). При
156
этом вектор будет все время перпендикулярен плоскости движения.
в общем случае, как и в араллельного движения, движения (в частности и
полюса не зависит.
скоростей и ускорений точек свободно движущегося тела можно использо-
вать результатыРис. 4.9. |
§ 4.2. |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Скорость |
vM |
любой |
|
точки |
М |
тела, |
как |
и в |
|||||
случае |
плоскопараллельного движения, |
склады- |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
вается |
из |
|
скорости vA |
полюса |
А и |
скорости |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
vMA , которую получает точка М, двигаясь вме- |
||||||||||||||
сте с телом вокруг полюса А, т. е. |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
vM |
vA |
vMA |
, |
|
|
(4.8) |
||
|
Правильность этого результата доказывает- |
|||||||||||||
ся |
так |
же, |
как |
в |
§3.2. |
Согласно |
(4.3), |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
vMA |
|
AM . Поэтому |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
vM |
vA |
( |
|
AM ) . |
|
(4.9) |
||
|
Аналогично для ускорения любой точки М |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
aM |
aA |
aMA . |
|
|
|
|
||
|
|
|
|
|
|
(4.10) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Здесь |
величина |
aMA |
определяется |
равенст- |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
AM , |
вом (4.5), в котором следует полагать |
r |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а v |
vMA |
|
|
AM . |
|
|
|
|
|
|
|
|
||
§ 4.4. Примеры решения задач
Пример 4.1. Определить скорости точек В и
157
