
Учебное пособие 1631
.pdf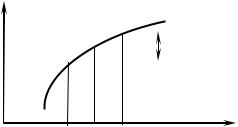
Например, функция y x2 6x 7 монотонно убывает на промежутке , 3 и монотонно возрастает на промежутке
3, . |
|
Функция y f x называется четной, если |
f x f x , |
и нечетной, если f x f x . График нечетной функции |
|
симметричен относительно начала координат, а нечетной функции — относительно оси Oy .
Функция y f x |
называется |
периодической, если |
||||
существует такое число T 0 , что |
для всех |
x |
из области |
|||
определения выполняется |
условие |
f |
x T f x . Число |
T |
||
называется периодом. |
|
|
|
|
|
|
Введем понятие предела функции. |
|
y f x при |
|
|||
Число A называется пределом функции |
x , |
|||||
стремящемся к а ( x a ), если для любого сколь угодно малого положительного ε > 0 найдется такое δ(ε) > 0, что для всех х,
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
удовлетворяющих |
|
|
неравенству |
x a |
|
имеет место |
|||||||||||||||
неравенство |
|
|
f x A |
|
. Если |
A есть предел функции y f x |
|||||||||||||||
|
|
||||||||||||||||||||
при x a , то пишут |
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim f x A . |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x a |
|
||||||
Определение |
предела |
функции y f x графически |
|||||||||||||||||||
иллюстрируется следующим образом (рис. 4). |
|
||||||||||||||||||||
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
А + |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
А |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
А – |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a – |
а |
|
a + |
x |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Рис. 4
30
Для сколь угодно малой -окрестности A ; A около
ординаты A найдется такая окрестность точки a , что для |
||||||
всех точек |
x |
из окрестности точки a |
a ; a |
точки |
||
графика |
функции |
y f x |
будут |
лежать |
внутри |
|
полосы A ; A . |
|
|
|
|
||
Число |
A |
называется пределом функции y f x при |
||||
x , если для любого сколь угодно малого ε > 0 найдется
такое N 0 , что |
для всех x N |
будет выполняться |
||||
неравенство |
|
f x A |
|
, что записывается |
||
|
|
|||||
|
|
|
|
|
lim f x A . |
|
|
|
|
|
|
x |
|
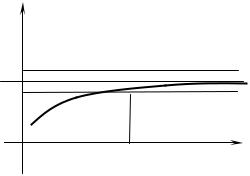
Графически это |
иллюстрируется |
следующим образом |
||||
(рис. 5). |
|
|
||||
у
A +
А
A –
О |
N |
х |
Рис. 5
Для сколь угодно малой -окрестности около ординаты A найдется такое значение N , что для всех x N график функции не будет выходить за пределы полосы A ; A .
Пределы обладают следующими свойствами:
1. Предел алгебраической суммы функций u x и v x равен алгебраической сумме пределов этих функций.
lim u x v x |
lim u x |
lim v x . |
x a |
x a |
x a |
31 |
|
|
Пример 3.1.
|
3x4 |
2x2 |
|
|
2 |
|
|
2 |
|
lim |
|
|
lim 3 |
|
|
|
lim 3 |
lim |
|
|
|
|
|
||||||
x |
|
x4 |
x |
|
x2 |
|
x |
x x2 |
|
2. Предел произведения функций u x и произведению пределов этих функций.
lim u x v x lim u x lim v x . |
||
x a |
x a |
x a |
3.
v x равен
|
Постоянный множитель можно выносить за знак предела |
lim cv x c lim v x . |
|
x a |
x a |
3. Предел частного от деления двух функций и v x равен частному от деления пределов этих функций
|
|
|
|
u x |
|
lim u x |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
x a |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
lim |
|
|
|
|
|
. |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
lim v x |
|
|
|
|
|
|
|
||||||
|
|
|
|
x a v x |
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
x a |
|
|
|
|
|
|
|
|
||
|
Пример 3.2. Вычислить предел lim |
4x2 |
5x 1 |
. |
|
|
|
|
|||||||||||||
|
3x |
4 |
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
x 3 |
|
|
|
|
|
|
||||
|
4x2 5x 1 |
|
lim 4x2 5x 1 |
|
|
4lim x2 |
5lim x lim1 |
|
15 |
||||||||||||
lim |
|
|
|
x 3 |
|
|
|
x 3 |
|
|
x 3 |
x 3 |
|
|
|
|
|||||
3x 4 |
lim 3x 4 |
|
|
|
|
|
|
|
|
||||||||||||
x 3 |
|
|
|
|
|
3lim x lim 4 |
|
|
|
5 |
|||||||||||
|
|
|
|
x 3 |
|
|
|
|
x 3 |
x 3 |
|
|
|
|
|
||||||
u x
3 .
Если при вычислении пределов алгебраической суммы, произведения или частного от деления функций сами функции стремятся к некоторым константам, не равным одновременно нулю в случае деления функций, то вычисление пределов не вызывает затруднения.
Пределы отношения бесконечно малых величин, отношения бесконечно больших величин, произведения бесконечно малой и бесконечно большой величины могут принимать различные значения или даже не существовать.
32
Выражения вида |
0 |
, |
|
, 0 , , 1 |
называются |
||
|
|
|
|||||
|
|
|
|
||||
|
0 |
|
|
|
|
||
неопределенностями.
Укажем приемы для «раскрытия неопределенности».
1. Пусть в числителе и знаменателе стоят многочлены, стремящиеся к бесконечности при x , т. е. чтобы убрать
неопределенность , необходимо выносить старшие степени
x в числителе и знаменателе дроби для последующего сокращения.
Пример 3.3.
|
|
|
|
|
x2 |
(3 |
7 |
|
|
1 |
|
) |
|
(3 |
7 |
|
1 |
) |
|
|||||||
|
3x2 7x 1 |
|
|
|
|
|
|
x2 |
|
|
|
x2 |
||||||||||||||
lim |
lim |
|
|
|
|
x |
|
|
|
|
lim |
|
x |
|
|
|
. |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
x 5x3 4x2 2 |
x |
|
|
3 |
4 |
2 |
|
|
x |
4 |
2 |
|
|
|
||||||||||||
|
|
|
|
|
x |
|
(5 |
|
|
|
|
) |
|
x (5 |
|
|
|
) |
|
|||||||
|
|
|
|
|
|
x |
|
x3 |
|
x |
x3 |
|||||||||||||||
Так как дроби вида |
|
const |
являются бесконечно малыми, |
|||||||||||||||||||||||
|
xn |
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
то в качестве слагаемых с числами 3 и 5 ими можно
пренебречь. Имеем lim |
|
3 |
|
0. |
|
|
|
|
|
|
|
|
|
|
|
||
x 5 |
х |
|
|
|
|
|||
2. Неопределенность вида |
0 |
|
получается при |
|||||
|
|
|
||||||
|
|
|
|
|
|
|
||
|
|
|
|
|
0 |
|
|
|
стремлении многочленов числителя и знаменателя к нулю при
х → а. Разложение на множители позволяет |
выделить |
|
в числителе и знаменателе бесконечно малые |
x а |
как |
множители для дальнейшего сокращения и избавления от неопределенности.
Пример 3.4.
lim |
x2 |
3x 10 |
lim |
(x 2) x 5 |
|
|
lim |
x 5 |
|
7 |
. |
|||
|
|
|
|
|
|
|
|
|
||||||
x 2 x2 5x 2 |
x 2 |
1 |
|
|
x 2 |
2x 1 3 |
|
|||||||
|
|
|
|
|
2(x 2) x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
33 |
|
|
|
|
|
|
|
|
|

3. Если дробь содержит иррациональные выражения, то
для того, чтобы убрать неопределенность |
0 |
, необходимо |
|
||
0 |
|
|
избавиться от иррациональности, домножая числитель и знаменатель на иррационально сопряженные выражения. Если корни квадратные, то числитель и знаменатель умножается на сопряженное выражение, тем самым получается разность квадратов. Если же корни кубические, то выражения доводятся до разности или суммы кубов.
Пример. 3.5.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
lim |
|
3x 1 2 |
|
lim |
( 3x 1 2)( |
3x 1 2) |
|
|
|
||||||||||||||||||||
|
|
2 4x 5 |
x 2 4x 5 ( |
|
|
2) |
|
|||||||||||||||||||||||
|
x 1 x |
|
|
|
|
x 1 |
3x 1 |
|
|
|
||||||||||||||||||||
|
lim |
|
|
(3x 1) 4 |
|
|
|
|
lim |
3 x 1 |
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
x 2 4x 5 ( |
|
|
|
|
|
|
|
4 x 1 x 5 |
|||||||||||||||||||||
|
x 1 |
3x |
1 2) |
x 1 |
|
|||||||||||||||||||||||||
lim |
|
|
(3x 1) 4 |
|
|
|
|
|
lim |
|
3 x 1 |
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
x 2 |
4x 5 ( |
|
|
|
|
|
|
2) |
|
4 x 1 x 5 |
|
|
|
|||||||||||||||||
x 1 |
3x 1 |
|
x 1 |
|
|
|
|
|
||||||||||||||||||||||
|
= lim |
3 |
|
|
|
1 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
x 1 |
4(х 5) |
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
4. Дробь содержит тригонометрические функции, |
|||||||||||||||||||||||||||||
которые при |
x 0 |
стремятся к нулю. Получается неопре- |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
деленность вида |
|
|
. |
Для решения необходимо восполь- |
||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
зоваться первым замечательным пределом lim |
sin x |
1 . |
|||||||
|
|
||||||||
|
|
|
|
x 0 |
x |
|
|
||
Пример. 3.6. |
|
|
|
|
|
|
|
|
|
lim |
sin 6x |
lim |
6sin 6x |
6 lim |
sin 6x |
|
6. |
||
|
|
|
|||||||
x 0 |
x |
x 0 |
6x |
x 0 6x |
|
|
|||
34
Пример. 3.7.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin 16x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
x |
16x |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
||||||||
|
x sin 16x |
|
|
|
|
16 |
|
|
|
|
x |
|
|
|
4 |
|
32 |
|
|||||||||||||||||
lim |
|
lim |
|
|
|
16x |
|
|
|
|
|
lim |
|
|
|
|
|
|
|
|
|
|
|
|
. |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
5x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
x 0 |
1 cos5x |
|
x 0 |
|
|
|
2 |
|
|
2 |
|
x 0 |
|
|
2 |
5x |
|
25x2 |
|
|
25 |
|
|||||||||||||
|
|
|
|
|
|
2sin |
|
|
|
|
|
|
|
|
|
|
|
sin |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
25x2 |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
5. Рассмотрим неопределенность 1 . Воспользуемся
вторым замечательным |
пределом |
lim(1 x)1/ x |
e или |
|||||||
|
|
|
|
|
|
|
x 0 |
|
|
|
lim(1 |
1 |
)x e , где e — иррациональное число (e 2,71828...) . |
||||||||
|
||||||||||
x 0 |
x |
|
|
|
|
|
|
|
|
|
|
|
|
x 5 |
2 x 7 |
x 4 9 |
2 x 7 |
|
|||
Пример 3.8. |
lim |
|
|
= lim |
|
|
= |
|
||
|
|
|
x x 4 |
|
x |
x 4 |
|
|
||
|
|
|
9 |
2 x 7 |
|
|
|
|
|
|
|
|
|
x 4 |
|
9 2 x 7 |
|
|
||||||||
|
|
|
|
|
|
|
9 |
|
9 |
x 4 |
|
|
|
|||||||||||||
= lim |
1 |
|
|
|
|
|
|
|
= lim 1 |
|
|
|
|
|
|
|
|
|
= |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
x |
|
|
x 4 |
|
|
|
|
x |
|
|
|
x 4 |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
9 2 x 7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
x 4 |
|
|
x 4 |
|
|
|
|
9 2 x 7 |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
9 |
|
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
18 |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
x |
lim |
|
x |
4 |
|
e . |
|
|
|||||||||
lim 1 |
|
|
|
|
|
|
|
e |
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
x 4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рассмотрим понятие непрерывности функции в точке. |
||||||||||||||||||||||||||
Функция у = f (х) непрерывна в точке х0 , если: |
|
|||||||||||||||||||||||||
1) функция определена в точке х0; |
|
|
|
|
|
|
|
|
|
|||||||||||||||||
2) существуют |
|
lim |
f (x) и |
|
lim |
|
|
|
f (x) ; |
|
|
|||||||||||||||
|
|
|
|
|
x x0 |
0 |
|
|
x x0 |
0 |
|
|
|
|
|
|
||||||||||
3) выполняется |
|
равенство |
|
|
|
lim |
|
|
|
f (x) = lim |
f (x) = |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x x0 0 |
|
|
|
|
x x0 |
0 |
||||||
= f (х0).
35
Если хотя бы одно из требований непрерывности не выполнено, то в точке х0 функция у = f(х) разрывна. Точка
х = х0 |
в этом случае называется точкой разрыва. |
|
|||||||||||
Если существуют конечные односторонние различные |
|||||||||||||
пределы |
lim |
f (x) |
lim |
f (x) , |
то |
х = х0 называется |
|||||||
|
|
x x0 0 |
|
|
|
x x0 0 |
|
|
|
|
|
||
точкой разрыва 1-го рода (скачок). |
|
|
|
||||||||||
Если |
хотя |
бы |
один |
из |
односторонних |
пределов |
|||||||
lim |
f (x) |
или |
lim |
f (x) |
не является конечным, |
то точка |
|||||||
x x0 0 |
|
|
|
x x0 0 |
|
|
|
|
|
|
|||
х = х0 |
является точкой разрыва 2-го рода. |
|
|
||||||||||
Рассмотрим понятия бесконечно малой и бесконечно |
|||||||||||||
большой функций. |
|
|
|
|
|
|
|
|
|
||||
Функция |
y f (x) |
называется |
бесконечно |
малой |
|||||||||
величиной при x a , если lim f (x) 0 . |
|
|
|||||||||||
|
|
|
|
|
|
|
x a |
|
|
|
|
|
|
Пример 3.9. Функция |
y |
1 |
будет бесконечно малой при |
||||||||||
|
|||||||||||||
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
x , так как lim |
1 |
0 . |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|||||||
|
|
|
x x |
|
|
|
|
|
|
|
|||
1. Сумма конечного числа бесконечно малых величин |
|||||||||||||
есть величина бесконечно малая. |
|
|
|
||||||||||
2. |
Произведение любого (конечного или бесконечного) |
||||||||||||
числа бесконечно малых величин есть бесконечно малая
величина. |
|
|
|
|
|
|
|||
|
|
|
3. Произведение бесконечно малой величины и ограни- |
||||||
ченной функции есть бесконечно малая величина. |
|
||||||||
|
|
|
Функция |
y f |
x |
называется |
бесконечно большой |
||
величиной при x a , |
если lim f x . |
|
|
|
|||||
|
|
|
Если f x |
|
|
x a |
|
|
|
|
|
|
является |
бесконечно |
малой |
величиной, |
то |
||
1 |
|
есть бесконечно большая величина. |
|
|
|||||
|
|
|
|
|
|||||
|
f x |
|
|
||||||
|
|
малая величина f x |
|
|
|
||||
|
|
|
Бесконечно |
является бесконечно |
|||||
малой величиной более |
высокого порядка |
малости |
по |
||||||
|
|
|
|
|
|
36 |
|
|
|

сравнению с |
бесконечно малой |
величиной x , если |
|||
lim |
f x |
0 . |
|
|
|
|
|
|
|
||
x a x |
|
f x и |
f x называются |
||
|
Бесконечно |
малые величины |
|||
бесконечно малыми величинами одного порядка малости при |
||||
x a , если lim |
f x |
C , где C |
является |
не равной нулю |
|
||||
x a x |
|
|
||
константой. |
|
|
f x и |
x называются |
Бесконечно |
малые величины |
|||
эквивалентными бесконечно малыми величинами при x a , |
|||||||||||||||
если lim |
f x |
|
1. |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
||||||
x a x |
|
|
|
|
|
|
|
|
|
|
|
||||
Пример 3.10. Бесконечно малые величины x |
и ln 1 x |
||||||||||||||
при x 0 являются эквивалентными, так как |
|
||||||||||||||
|
lim |
ln 1 x |
|
lim |
1 |
ln 1 x lim ln 1 x 1/ x |
ln e 1. |
||||||||
|
|
|
|
||||||||||||
|
x 0 |
|
x |
|
|
x 0 x |
x 0 |
|
|||||||
При вычислении пределов бесконечно малые величины |
|||||||||||||||
могут заменяться эквивалентными. |
|
||||||||||||||
Основные эквивалентности: |
|
|
|||||||||||||
1. |
x ~ |
sin x ~ |
tgx |
~ e x 1 |
~ ln(1 x) . |
|
|||||||||
|
|
|
x 0 |
|
|
x 0 |
|
x 0 |
x 0 |
|
|||||
2. |
(1 cos x) |
~ |
|
x2 |
2 |
. |
|
|
|
|
|||||
|
|
|
|
|
|
|
x 0 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
3. |
log a 1 x ~ |
x log a e . |
|
|
|||||||||||
|
|
|
|
|
|
|
x 0 |
|
|
|
|
|
|
||
4. |
a x 1 ~ |
x ln a . |
|
|
|
|
|
|
|||||||
|
|
|
|
|
x 0 |
|
|
|
|
|
|
|
|
|
|
5. |
1 x k 1 ~ kx . |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
x 0 |
|
|
|
|
|
|
||
|
|
|
|
x |
|
|
|
|
|
|
|||||
6. |
k 1 x 1 ~ |
. |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
x 0 |
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
37 |
|
|
||
|
Пример 3.11. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
lim |
sin2 5x |
lim |
25x2 |
|
25 |
lim x 0 . |
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
x 0 tg 2x |
|
x 0 |
2x |
|
2 x 0 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
Пример 3.12. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
lim |
log2 1 sin x |
lim |
|
log2 1 x |
log2 e . |
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
x 0 |
|
|
|
|
|
|
|
|
x 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
Пример 3.13. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
lim |
|
7x |
6x |
lim |
7x 1 1 6x |
|
lim |
|
7x |
1 6x 1 |
|
|||||||||||||||||||||||||||||
|
|
|
|
|
3x |
|
x2 3x |
|
|
|
|
|
|
|
x2 |
3x |
|
|||||||||||||||||||||||||
|
|
x 0 x2 |
|
x 0 |
|
|
|
|
x 0 |
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x ln 7 x ln 6 |
|
|
|
|
x ln |
|
|
|
|
|
7 |
|
|
1 |
|
|
1 |
|
|
5 |
|
|||||||||||||||||||
|
lim |
|
lim |
|
6 |
|
|
|
ln |
lim |
|
|
|
ln |
|
. |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
x 0 |
|
x2 3x |
|
x 0 x x 3 |
6 |
|
x 0 x |
3 3 4 |
||||||||||||||||||||||||||||||||
|
Рассмотрим понятие производной функции и правила ее |
|||||||||||||||||||||||||||||||||||||||||
вычисления. |
|
|
|
|
|
|
|
y f x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
Пусть |
|
|
функция |
|
определена |
|
в |
некотором |
|||||||||||||||||||||||||||||||||
промежутке. |
Функция y f x |
называется дифференцируемой |
||||||||||||||||||||||||||||||||||||||||
в точке |
x , |
|
|
если приращение функции y |
|
при приращении |
||||||||||||||||||||||||||||||||||||
аргумента |
x |
имеет вид y A x ( x) , |
где |
A не зависит |
||||||||||||||||||||||||||||||||||||||
от x , а |
( x) является бесконечно малой |
более высокого |
||||||||||||||||||||||||||||||||||||||||
порядка малости по сравнению с x . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
Для дифференцируемой функции предел отношения |
|||||||||||||||||||||||||||||||||||||||||
приращения функции y к вызвавшему |
|
это |
|
приращение |
||||||||||||||||||||||||||||||||||||||
приращению |
|
|
аргумента |
|
|
|
|
x , |
|
|
|
при |
|
|
|
x 0 , |
|
т. е. |
||||||||||||||||||||||||
lim |
y |
|
|
lim |
|
A x ( x) |
A |
|
|
|
называется |
производной |
||||||||||||||||||||||||||||||
x |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
x 0 |
|
x |
0 |
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
функции |
f(x) |
по |
|
независимой |
переменной |
x, |
обозначается |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
38 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||

f (x), |
y , |
dy |
. Операцию |
нахождения производной назы- |
|
||||
|
|
dx |
|
|
вают дифференцированием. |
|
|||
Если функция y f x |
дифференцируема, то она непре- |
|||
рывна. Обратное утверждение неверно, т. е. непрерывная функция может не иметь производную в этой точке.
Производная имеет геометрический смысл. Значение производной f x при данном значении аргумента x равняется
тангенсу угла, образованного с положительным направлением |
|||||||||||||||||||||||||||||||||
оси Оx касательной к |
графику функции f |
x |
в соответ- |
||||||||||||||||||||||||||||||
ствующей точке M x, y . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
С другой стороны, производная функции есть скорость |
|||||||||||||||||||||||||||||||
изменения этой функции. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
Основные формулы дифференцирования |
|
|
|
|
|||||||||||||||||||
1. |
y const , |
|
|
|
y' 0 . |
9. (sin x) cos x . |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
2. |
(xn ) nxn 1 . |
10. |
(cosx) sin x . |
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
||
3. |
( |
|
|
x ) |
|
|
|
|
|
|
. |
|
11. |
(tgx) |
|
|
|
|
|
. |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
cos2 x |
|
|
|
|
|
|
||||||||||||||||||
|
2 |
|
|
x |
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
12. |
(ctgx) |
|
|
1 |
. |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
4. |
|
|
|
|
|
|
|
|
. |
|
|
|
|
sin |
2 |
x |
|
|
|
|
|
|
|||||||||||
|
x2 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
5. |
(e x ) e x . |
|
|
|
|
|
13. |
(arcsin x) |
|
|
|
|
1 |
|
|
|
|
. |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 x2 |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
6. |
(a x ) a x ln a . |
14. |
(arccosx) |
|
|
|
|
1 |
|
|
|
. |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 x2 |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
7. |
(ln x) |
|
1 |
. |
|
|
|
|
|
15. |
(arctgx) |
|
|
1 |
|
|
. |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
x2 |
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|||||||
8. |
(log |
x) |
|
|
1 |
. |
16. |
(arcctgx) |
|
|
1 |
. |
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
a |
|
|
|
|
|
|
x ln a |
|
|
|
|
1 x2 |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
39 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
