Учебное пособие 941

волны λ равна такому расстоянию, на которое распространяется определенная фаза волны за

где Т - период, ν = 1/Т - частота волны, ϑ – скорость распространения волны

Уравнением упругой волны называется выражение, кото-

рое дает смещение ξ колеблющейся частицы среды, заданной координатами равновесного положения х, у, z в произвольный момент времени:

ξ = ξ(x,y,z,t).

Получим вид уравнения плоской волны, распространяющейся вдоль оси Х. Волновые поверхности представляют собой плоскости, перпендикулярные оси Х.

Все точки выбранной волновой поверхности колеблются одинаково. Смещение ξ всех точек этой плоской поверхности будет зависеть от ее координаты х и времени t: ξ=ξ(х,t). Пусть точки плоскости x = 0 (рис. 14) совершают колебания по зако-

ну

ξ(0,t) = a cos(ωt+α).

Найдем закон колебаний точек в плоскости, соответствующей произвольному значению х. Для того, чтобы пройти путь от плоскости х = 0 до этой плоскости, волне требует-

ся время τ = x/ϑ . Следовательно, колебания частиц лежащих в

плоскости х, будут отставать на время τ от колебаний частиц в плоскости х = 0, т.е. будут совершаться по закону

ξ(x,t) = a cos[ω(t-τ)+α] = a cos[ω(t-x/ϑ )+α].

Итак, уравнение плоской волны (как продольной, так и поперечной), распространяющейся в направлении оси х, получает вид:

21

название фазовой скорости волны.

Из равенства (44) следует, что скорость распространения

Согласно (44), dx/dt>0. Следовательно, уравнение (42) описывает волну, распространяющуюся в сторону возрастания

.

Волна, распространяющаяся в противоположном направлении, определяется уравнением:

ξ = a cos[ω(t+x/ϑ )+α]. (46)

Уравнению (46) можно придать симметричный вид относительно переменных х и t. Для этого введем величину

и назовем ее волновым числом. Умножая числитель и знамена-

тель выражения (47) на частоту ν, представляем волновое число в виде:

Раскрывая в (42) круглые скобки и принимая во внимание (48), придём к следующему уравнению плоской волны, распространяющейся вдоль положительного направления оси x

Уравнение плоской волны, распространяющейся в противоположную сторону, отличается от (49) только знаком при члене kx.

Уравнение плоской волны является решением некоторого дифференциального уравнения, называемого волновым. В декартовых координатах волновое уравнение плоской волны имеет вид:

∂2ξ2 + ∂2ξ2 + ∂2ξ2 = 12 ∂2ξ2

∂x ∂y ∂z ϑ ∂t

Здесь ξ смещение частицы среды с координатами x,y,z в момент времени t.

Отметим, представленные уравнения распространяющейся плоской волны справедливы для сред без поглощения.

Если размеры изотропного источника упругой волны малы, то на большом расстоянии от него волновые поверхности будут образовывать семейство сфер с общим центром в точке положения источника (семейство концентрических сфер).

Уравнение сферической волны при отсутствии поглощения средой имеет вид

(50)

Здесь 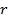- расстояние от точечного источника до заданной точки (x,y,z); - амплитуда колебаний частиц на расстоянии r = 1м, k = ωϑ = 2λπ - волновое число.

23

2.2. Скорость волны в различных средах

При распространении упругих волн происходит деформация среды. При продольных волнах - деформация растяжения и сжатия, при поперечных – сдвига. Если деформировать (сжать, растянуть или сдвинуть относительно друг друга) крайние точки тела, то эта деформация будет распространяться в теле с некоторой скоростью ϑ . Эта скорость будет определяться взаимодействием молекул или атомов в среде – чем больше взаимодействие, тем больше скорость. Таким образом, максимальная скорость будет в твердых телах, минимальная – в газах.

Можно показать, что скорость продольной волны в твердых телах равна

, (51)

а поперечных –

. (52)

Здесь Е – модуль Юнга, G – модуль сдвига среды, ρ - плотность тела.

Выражение z = Eρ называется волновым сопротивлени-

ем или импедансом среды.

Скорость упругих волн в жидкостях и газах равна

щенной среды. Модуль объемной упругости для определенной жидкости или реального газа находится экспериментально. Если процесс объемной деформации жидкости или газа при распространении в них упругих волн считать адиабатным, то для

идеального газа K = γ p, где p – давление невозмущенного газа, γ

– показатель адиабаты.

Если учесть, что плотность идеального газа равна

24

ρ = MPRT ,

где М – молярная масса, R – газовая постоянная и T – абсолютная температура, то для скорости звука в идеальном газе получим

При нормальных условиях (p = 105 Па, Т = 300 К) атмосферный воздух по своим свойствам подобен идеальному газу. Отсюда получим оценку скорости звука в воздухе, для которого

2.3. Энергия упругой волны

Пусть в некоторой среде вдоль оси Х распространяется плоская продольная волна

Выделим в среде элементарный объем ∆V, настолько малый, чтобы скорость движения и деформацию во всех точках этого объема можно считать одинаковыми и равными, соответствен-

но, ∂ξ/∂t и ∂ξ/∂x.

Выделенный объем обладает кинетической энергией:

(ρ∆V-масса объема, ∂ξ/∂t- скорость движения точек среды). Рассматриваемый объем обладает также потенциальной энергией упругой деформации:

25

∆Wp = Eε22∆V = E ∂∂ξx2 2∆V

(57)

(ε = ∂ξ/∂x-относительная деформация, Е - модуль Юнга среды). Заменим в (57), полагаясь на формулу υ =, модуль Юнга на

ρ υ2 (ρ - плотность среды, υ – фазовая скорость волны). Тогда потенциальную энергию колеблющихся частиц среды в объеме

∆V можно представить в виде

Выражения (56) и (58) в сумме дают полную энергию выделяемого объёма

Разделив эту энергию на объем ∆V, в котором она содержится, получим плотность энергии

Из (60) следует, что плотность энергии в каждый момент времени в разных точках пространства различна. Средняя плот-

Здесь учтено, что среднее значение квадрата синуса за пе-

риод равно 1/2, т.е. <sin2 (ωt-кх)>=1/2.

26

Видно, что плотность энергии пропорциональна плотности

среды ρ, квадрату частоты и квадрату амплитуды волны.

Итак, среда, в которой распространяется волна, обладает дополнительным запасом энергии. Эта энергия доставляется от источника колебаний в различные точки среды самой волной.

Количество энергии, переносимое волной через некоторую поверхность в единицу времени, называется потоком энергии через эту поверхность. Если через данную поверхность за время dt переносится энергия dW, то по определению поток энергии будет равен

Поток энергии в разных точках среды может быть различной интенсивности.

Для характеристики переноса энергии в различные точки пространства вводится векторная величина, называемая плотностью потока энергии. Эта величина численно равна потоку энергии через единичную площадку, помещенную в данной точке перпендикулярно к направлению, в котором переносится энергия. Направление вектора плотности потока энергии совпадает с направлением переноса энергии. Модуль потока энергии равны

Через площадку ∆S (рис.15) будет перенесена за время ∆t энергия ∆W, заключенная в объеме цилиндра с основанием ∆S и

высотой ϑ ∆t (ϑ – фазовая скорость волны). Если размеры цилиндра достаточно малы, чтобы плотность энергии во всех точках цилиндра можно было счи-

тать одинаковой, то ∆W можно найти, как произведение плотно-

сти энергии w на объем цилиндра ∆S ϑ ∆ t: ∆W = w∆S v∆t. Подставив это выражение в формулу (63), получим для плотности потока энергии:

27

Наконец, введя вектор , модуль которого равен фазовой

скорости волны, а направление совпадает с распространением волны (переноса энергии), можно написать

Этот вектор называется вектором Умова. Среднее значение плотности потока энергии равно

Отметим, что когда говорят об интенсивности волны в данной точке, то имеют в виду среднее по времени значение плотности потока энергии, переносимое волной.

2.4. Стоячие волны

Если в среде распространяется одновременно несколько волн, то колебания частиц среды оказываются геометрической суммой колебаний, которые совершали бы частицы при распространении каждой из волн в отдельности. Следовательно, волны просто накладываются одна на другую. Это утверждение назы-

вается принципом суперпозиции (наложения) волн.

В случае, когда колебания, обусловленные отдельными волнами в каждой точке среды, обладают постоянной разностью фаз, волны называются когерентными (согласованными).

При сложении когерентных волн возникает явление интерференции, заключающееся в том, что колебания в одних точках усиливают, а в других точках ослабляют друг друга.

Очень важный случай интерференции наблюдается при наложении двух встречных плоских волн с одинаковой амплитудой. Возникающий в результате колебательный процесс называется стоячей волной. Практически стоячие волны возникают при отражении волн от преград. Падающая на преграду волна и бегущая ей навстречу отраженная волна, налагаясь друг на друга, дают стоячую волну.

28

Напишем уравнение двух плоских волн, распространяющихся вдоль оси х в противоположных направлениях

Сложив эти уравнения и преобразовав результат по фор-

муле

называемое уравнением стоячей волны. Из (68) видно, что в каждой точке стоячей волны происходит колебание той же частоты, что и у встречных волн, причем амплитуда зависит от х:

Аст = 2a cos( 2λπx ).

В точках, координаты которых удовлетворяют условию

2λπx = ± nπ, (n = 0,1,2,…),

амплитуда колебаний достигает максимального значения. Эти точки называют пучностями стоячей волны.

Для координат пучностей получаем:

При этом отметим, что пучность представляет собой не одну единственную точку, а плоскость, точки которой имеют одну и ту же координату, определяемую формулой (69).

В точках, координаты которых удовлетворяют условию

амплитуда колебаний обращается в ноль. Эти точки называются узлами стоячей волны. Точки среды, находящиеся в узлах, колебаний не совершают (рис.16). Координаты узлов имеют значения:

29

Продифференцировав уравнение стоячей волны

ξ = ξ(x,t) один раз по t, а другой раз по x, найдем выражение для скорости частицы и для деформации среды ε в точках х:

Рис.16 Рис.17

Уравнение (71) описывает стоячую волну скорости, а (72)

– стоячую волну деформации (см. рис. 17).

На рис.17 сопоставлены «моментальные фотографии» смещения ξ(x), скорости ∂ξ/∂t и деформации ∂ξ/∂x для моментов

времени 0 и π/4. Из графиков видно, что узлы и пучности скорости совпадают с узлами и пучностями смещения; узлы же и пучности деформации совпадают соответственно с пучностями

и узлами смещения. В то время, как ξ и ε достигают максималь-

ных значений, ξ обращается в ноль и наоборот. Соответственно дважды за период происходит превращение энергии стоячей волны то полностью в потенциальную, сосредоточенную вблизи узлов волны, то полностью в кинетическую, сосредоточенную в основном вблизи пучностей волны. В результате происходит

30