Методическое пособие 612

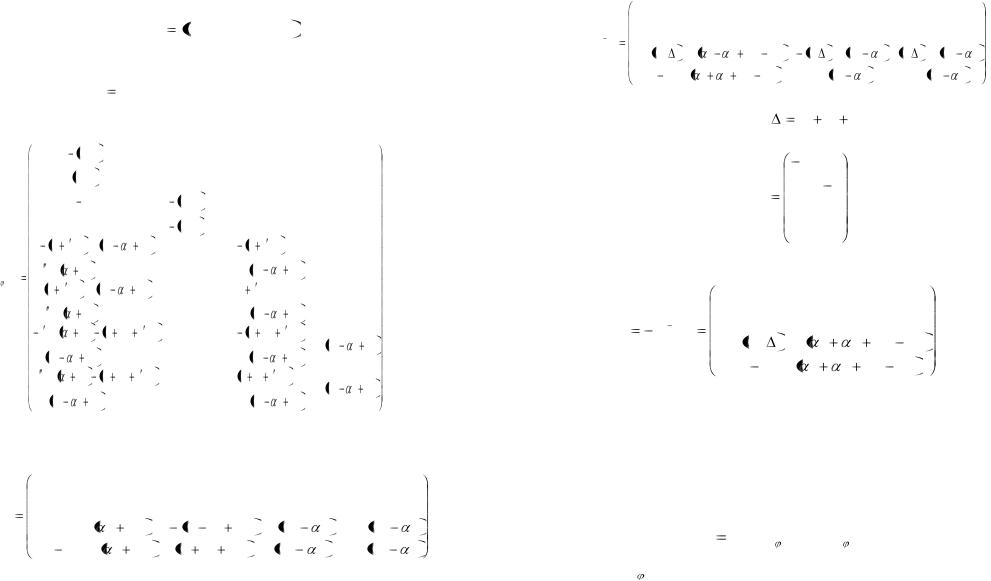
(3.33), определяющую связи в частично разомкнутой цепи, причем

Предполагая, что масса звеньев сосредоточена в их центрах, имеем,

Mx diag(m1 E 2 m2 E 2 m3 E 2 m4 E 2 ).

Определим якобиеву матрицу

найти путем непосредственного дифференцирования уравнений связи и определения из них зависимости p от q . Кинетическая энергия механизма в новых координатах равна:

Где J (p) определяется формулой (3.46). Вычисляя про-

изводные матрицы

100

можно получить движение механизма, используя уравнение

(3.15):

решая его совместно с уравнениями связи (3.44). Эту задачу, как мы видели, можно решать с помощью множителей Лагранжа, т.е. применяя уравнения Лагранжа первого рода.

Согласно рассмотренному выше подходу, следует вернуться к переменным q и записать кинетическую энергию в виде

Теперь можно интегрировать непосредственно уравнения

~

(3.41), определяя производные от матрицы A(q) с учетом формул,

приведенных в § 3.1. Поскольку эта матрица зависит от р, то на каждом шаге необходимо решать уравнения связей (3.44), определяя новые значения обобщенных координат р, соответствующие полученным при интегрировании на одном шаге значениям q. Приближенно эта задача может быть решена путем линеаризации уравнения связи в форме (3.30).

При достижении координатами предельных значений pi*, обусловленных конструкцией механизма, происходит наложение дополнительных связей на его движение. К уравнению (3.32) в этом случае добавляют pi = const = pi* , что приводит к изменениям

матрицы J (p) и выражения для кинетической энергии К.

~

Обозначим p значения скоростей обобщенных координат в момент, предшествующий удару, J * (p) — соответствующую мат-

рицу, вычисленную после наложения связи. Тогда, согласно теореме Карно, в предположении, что удар является абсолютно неупругим, получим

Отсюда можно найти начальные значения производных р0 для последующего интегрирования уравнений движения с наложенными связями и производных

Аналогичный подход следует применять и при наложении внешних связей, например при сборке. В момент удара необходимо определить новые начальные значения скоростей обобщенных координат в соответствии с теоремой Карно, после чего интегрировать уравнения движения с наложенными связями тем или иным способом.

3.3.Принцип Гаусса

3.3.1.Общая формулировка принципа Гаусса

Как известно, уравнения движения могут быть получены на основе вариационных принципов механики. Принцип Гаусса относится к числу вариационных принципов дифференциального типа. Он является наиболее общим принципом механики

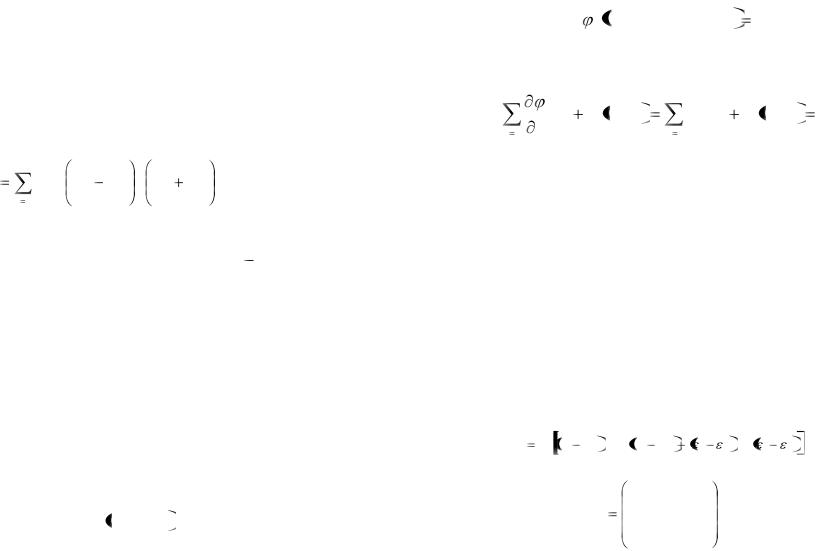
и позволяет получить уравнения движения системы при наложенных связях, как голономных, так и неголономных. Напомним, что принцип Даламбера — Лагранжа справедлив только для голономных и линейных голономных связей. В основе принципа Гаусса лежит понятие принуждения (Zwang), под которым понимают меру отклонения истинного движения, происходящего при наложении связей, от свободного движения, которое имело бы место в их отсутствие. В частности, для системы материальных точек с массами mi i = 1, 2, . . . , N , принуждение определяют следующим образом:

корение свободного движения. Таким образом, принуждение — это скалярная величина, имеющая в каждый момент времени смысл среднего (для системы материальных точек) квадратичного отклонения истинного ускорения от ускорения свободного движения.

Принцип Гаусса заключается в том, что в каждый момент времени истинное движение системы происходит таким образом, что принуждение минимально.

Поскольку единственными переменными в выражении (3.50) являются ускорения, то в соответствии с принципом Гаусса эти ускорения выбирают из условия минимального принуждения

при дополнительных ограничениях, определяемых уравнениями связей. В общем случае эти связи могут быть нелинейными и него- лоном-ными, и их уравнения имеют вид

Продифференцировав левую часть этого равенства по t, получим выражение вида

Итак, задача сводится к определению ускорений w j из

условия минимума выражения (3.50) при линейных относительно wj ограничениях (3.53). Эту задачу можно решить с помощью множителей Лагранжа, однако значительно более эффективным приемом является непосредственная (численная) минимизация принуждения, например с использованием методов динамического программирования.

3.3.2. Применение принципа Гаусса для исследования движения манипуляционных механизмов

Рассмотрим понятие принуждения для манипуляционного механизма. Для каждого из звеньев механизма, совершающих одновременно поступательное движение с ускорением wf и вращательное с ускорением £,, меру принуждения можно определить следующим образом:

моменты, приложенные к звену двигателем соответствующей степени подвижности и направленные вдоль орта оси zi, соответствующей кинематической пары; ~i , — угловые скорости звень-

Для всего механизма меру принуждения определяют так:

матрица масс и моментов инерции звеньев. Теперь задача сводит-

определяющих взаимное положение звеньев. Эти уравнения имеют вид

где rc — вектор центров масс звеньев.

Дважды продифференцировав правую часть этих уравнений, мы в п. 3.1 получили выражение для ускорения (3.38), которое в данном случае определяет наложенные на движение звеньев свя-

приложенных к звеньям в свободном движении, то уравнения

(3.59). Заметим, что положения, и скорости звеньев на каждом шаге вычисляются по ускорениям, определенным на предыдущем шаге. Таким образом, задача минимизации решается только для ускорений.

3.3.3. Определение ускорений вынужденного движения

Итак, при использовании принципа Гаусса задача сводится к определению ускорений истинного движения, минимизирующих принуждение. Эту задачу можно решить несколькими способами. Во-первых, можно получить выражение функции принуждения от

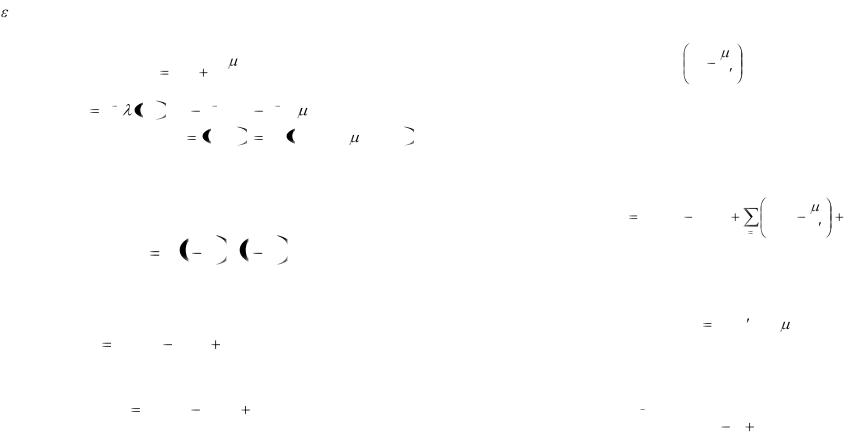
ускорений обобщенных координат q и рассмотреть методы его

численной минимизации. Во-вторых, можно использовать метод неопределенных множителей Лагранжа. Рассмотрим вначале пер-

(3.61)

причем функции Фi, определяются как правые части равенств (3.60). Теперь полученные выражения можно подставить в фор-

мулу

В последнем выражении мы выписали только слагаемые, зависящие от q . Вид остальных слагаемых, зависящих от обобщенных координат, их производных и внешних сил, не имеет значения при минимизации Z относительно ускорений q .

Во многих случаях полученное выражение нуждается в уточнениях, так как в кинематических парах могут действовать и другие силы, которые не учитываются нашей приближенной моделью. Например, при использовании двигателей постоянного тока с редуктором в выражении Z возникают дополнительные составляющие, обусловленные моментом инерции I’i вращающихся частей редуктора и ротора

приведенный к валу нагрузки момент инерции вращающихся частей (см. далее гл. 7) или же добавляя дополнительные слагае-

Задача состоит теперь в минимизации выражений (3.63) или (3.64) с учетом уравнения связей (3.59). Заметим, что в отсутствие связей, исходя из необходимого условия минимизации выражения (3.64), получим уравнения движения системы свободных тел

x Ф , Ii qi 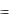i i=1,..,N

Рассмотрим задачу об определении ускорений путем минимизации квадратичной формы (3.64) с учетом линейных ограничений (3.59) методом динамического программирования [45].

Пусть Z k 1 — функция принуждения для механизма, со-

стоящего из последних N k 1 звеньев кинематической цепи манипулятора (т.е. от k-го звена до N -гo — схвата):

(3.65)

где Ii. — элементы диагональной (блочной) матрицы I .

В соответствии с основным принципом динамического программирования минимизация Zk позволяет записать следующее рекуррентное соотношение:

где Zk+1 — минимальное значение, полученное на предыдущем шаге минимизации.

В свою очередь, ускорение xk с помощью соотношений, по-

лученных в § 3.1, может быть рекуррентно вычислено по формуле вида

в которой матрица Ak и векторы Bk, Ck зависят только от обобщенных координат и их первых производных. Таким образом,

(остальные слагаемые на данном шаге вычислений уже известны).

Дифференцируя выражение, стоящее в квадратных скобках, по qk и приравнивая результат к нулю, получим ускорение qk , минимизирующее правую часть равенства (3.68):

щенные координаты qk и их первые производные qk . На первом шаге с учетом (3.67), (3.69) определяется ускорение в последней степени подвижности q N из рассмотрения движения N-го звена

(схвата) под действием внешних и управляющих сил и моментов. Далее определяют матрицы, входящие в правую часть равенства (3.69), и ускорения qk при k = N - 1, N -2, ..., 0. После двукратного интегрирования ускорений на одном шаге и определения новых значений qk , qk процедуру повторяют.

Итак, рассмотренная численная процедура позволяет осуществить моделирование движения манипуляционного механизма. Более подробно она описана А. Ф. Верещагиным в [45], где решение задачи обобщено на случай, когда на движение схвата наложены дополнительные ограничения (например, при движении по поверхности), а также на случай, когда подвижно основание манипулятора. Там приведены также рекуррентные формулы для вычисления матричных коэффициентов уравнения (3.69), значительно упрощающие процедуру вычислений.

Кратко остановимся на процедуре минимизации принуждения Z с использованием метода Лагранжа. В этом случае для того, чтобы найти движение, минимизирующее Z и совместимое со свя-

Заметим, что подставив в это уравнение выражение х через производные обобщенных координат по формуле (3.59), вновь получим уравнение движения в форме уравнения кинетостатики (5.52). Преимущество метода Гаусса достигается, таким образом, именно в тех случаях, когда используются численные методы минимизации функции принуждения на каждом шаге интегрирования уравнений движения.

Контрольные вопросы и задания

1.При каких условиях справедливы уравнения Лагранжа? Сопоставьте области применения модели динамики манипулятора в форме Лагранжа и в форме Даламбера (см. гл. 5).

2.Запишите уравнения движения манипулятора в форме уравнений Лагранжа первого рода для случая, когда схват перемещается в вертикальной плоскости.

3.Каким образом можно составить уравнения Лагранжа для манипулятора, механизм которого содержит замкнутые контуры?

4.Как учитывается явление абсолютно неупругого удара при моделировании уравнений динамики манипулятора?

5.Сформулируйте принцип Гаусса для системы материальных точек и манипуляционного механизма. Каковы

условия применимости этого принципа?

3.Составьте выражение, из которого путем минимизации можно найти ускорения обобщенных координат манипулятора для случая плоского двух-звенного механизма с вращательными парами.

7.Каким образом в выражении для принуждения по Гауссу можно учесть моменты инерции роторов двигателей вращательных степеней подвижности манипулятора?

8.Составьте алгоритм моделирования динамики манипулятора, согласно принципу Гаусса, с минимизацией принуждения методом динамического программирования (приведите пример).

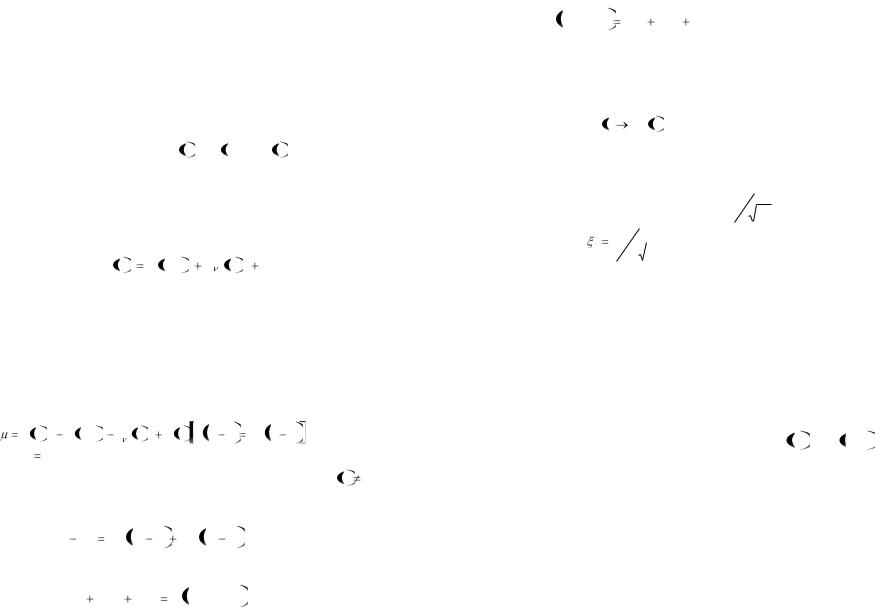
4. МЕТОДЫ, ОСНОВАННЫЕ НА РЕШЕНИИ ОБРАТНЫХ ЗАДАЧ ДИНАМИКИ

К обратным задачам динамики относят задачи, связанные с вычислением сил и моментов по заданному движению. Этот подход используется и в данном случае. Обратимся к уравнению динамики манипулятора в форме Даламбера (5.52). Будем считать, что известны желаемая траектория движения и соответствующие ей законы изменения обобщенных координат, их скоростей и ускорений q0 t , q 0 t и q 0 t , полученные

в результате процедуры планирования траектории Ограничимся случаем, когда внешние моменты отсутст-

вуют, а внешние силы представлены только силами тяжести звеньев и нагрузки, которые заранее известны. Таким образом, уравнение динамики манипулятора запишем в виде

Если задано движение манипулятора, т.е. векторы q , q , и q в функции времени, то из этого уравнения можно определить необходимые управляющие силы и моменты — вектор µ

. В этом состоит существо рассматриваемых здесь методов. 4.1. Компенсация динамики манипулятора в реальном вре-

мени Выберем вектор управляющих сил и моментов, исполь-

зуя формулу

функция, зависящая от выбора программной траектории. Нетрудно выбрать такие значения параметров матриц

K , К2, чтобы решение уравнения (4.3) для каждой степени подвижности манипулятора было асимптотически устойчивым. Тогда q t q0 t , т.е. процессы в системе стремятся к

своим программным значениям.

Можно обеспечить и заданные показатели качества переходных процессов. Действительно, для z-й степени подвиж-

ности постоянная времени Ti 1 k1i , а коэффициент демп-

k1i k2i, если заданы требования по времени переходного процесса и показателю колебательности (см. п. 3.2) для г-го канала управления. Поскольку определенная таким образом динамическая система состоит из N автономных каналов с желаемыми характеристиками, требование к каждому каналу управления нетрудно определить из обобщенных требований, предъявляемых к движению схвата манипулятора (см. п. 3.3).

Полностью реализовать управление (4.2) невозможно по ряду причин. Прежде всего, для этого потребовалось бы вы-

числять в реальном времени матрицы A q и , которые должны быть точно известны. Практически их можно определить для конкретного манипулятора лишь с известной степенью приближения. Вычисление этих матриц, к тому же, настолько сложно (см. гл. 5), что это обычно превосходит возможности управляющих устройств. Наконец, для того чтобы

скомпенсировать соответствующие слагаемые, зависящие от q и q, их следовало бы вычислить к моменту компенсации, совпадающему с моментом измерения, что невозможно.

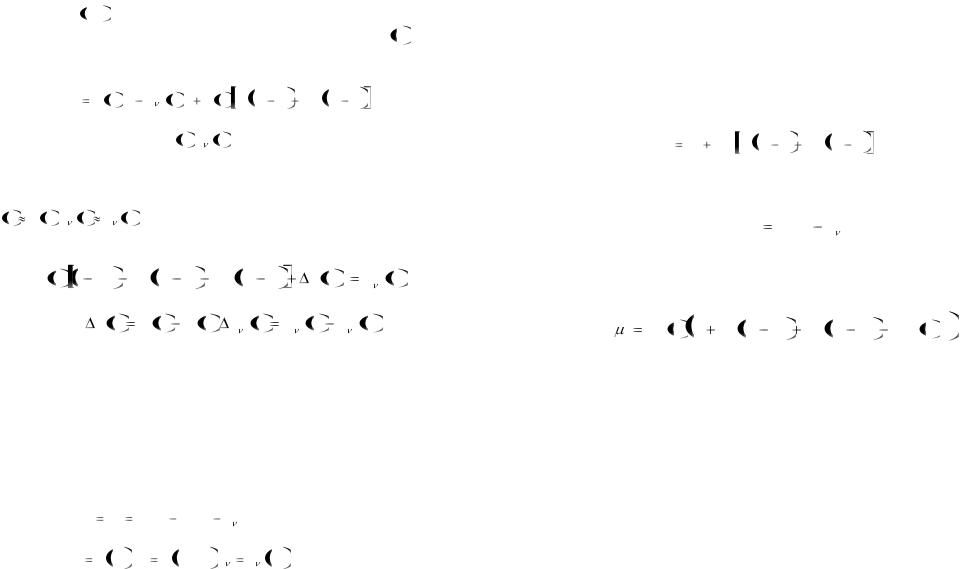
Тем не менее такое управление в ряде случаев можно рассматривать как идеализированную модель, к которой можно приближаться. Например, в тех случаях, когда влияние слагаемых B q, q q , определяющих относительные и кориоли-

совы ускорения, значительно меньше, чем слагаемых A q q , определяющих силы и моменты инерции, можно положить

что даже небольшие погрешности при расчетe управляющих моментов приводят к быстрому накоплению ошибок. Так, при

уравнении (4.1) слагаемым, зависящим от скорости, вместо

Следовательно, погрешность в правой части будет дважды интегрироваться по времени, что и приведет к накоплению ошибки.

4.2. Компенсация динамики программного движения

Из уравнения (4.1) следует, что для реализации программного движения необходимо развить в степенях подвижности манипулятора силы (моменты)

Непосредственная, без обратной связи реализация такого управления не даст ожидаемого результата, так как незначительные и неизбежные погрешности в вычислении µ0 приведут в результате интегрирования дифференциального уравнения второго порядка (4.1) к быстрому накоплению ошибок. Программное задание сил по этой причине никогда само по себе не приводит к программному изменению координат. Однако и в этом случае можно поступить также, как в п. 4.1.1, выбрав своеобразный моментный регулятор по формуле, аналогичной (4.2):

Как и ранее, в данном случае возможны упрощения. Например, пренебрегая вторым слагаемым в правой части выражения (4.5), получаем

μ0 A0q0 B0T G.

если к тому же можно пренебречь и перекрестными связями, обусловленными динамикой механизма, то формулы для управляющих сил (или моментов) приобретают особенно простой вид

Обоснованность тех или иных упрощений можно установить путем предварительного моделирования уравнений движения манипулятора.

Реализация управляющих моментов (4.5), (4.6) не представляет трудности в вычислительном отношении, поскольку заранее были рассчитаны все матричные коэффициенты. Однако в этом случае уже не происходит полной компенсации динамики манипуляционного механизма и вместо уравнения (4.3) получим нелинейное уравнение вида

116

ренциальное уравнение в отклонениях от программного движения:

это решение асимптотически устойчиво, то асимптотически устойчиво и решение q 0 t уравнения (4.7), т.е. программное

движение, реализуемое с помощью выбранного управления. Для того чтобы исследовать устойчивость тривиального

решения уравнения (4.8), выполним его линеаризацию в окрестности этого решения. Сохраняя принятые в § 3.1 обозначения, получим

т.е. матричное дифференциальное уравнение второго порядка (или систему нелинейных дифференциальных уравнений порядка 2N вида:

уравнения с переменными коэффициентами (4.9). В частности, в окрестности отдельных точек траектории, например конечной ее точки, устойчивость определяется расположением кор-

117

условие Re i 0 , то отклонения, обусловленные неточностью

компенсации динамических составляющих, стремятся к нулю с течением времени. Итак, в случае использования приближенных формул (4.5), (4.6) для вычисления управляющих сил и моментов, необходимо убедиться в устойчивости получаемой при этом системы.

4.3. Проблема реализуемости

Обратим теперь внимание на то, что представленные в п. 4.1.1 и 4.1.2 способы управления основаны на непосредственном формировании управляющих сил и моментов согласно одному из рассмотренных законов. Это возможно, например, при использовании высокомоментных безредукторных электродвигателей «прямого управления» (о которых упоминалось в гл. 5) или электрогидравлического привода. В настоящее время манипуляторы чаще всего оснащают высокооборотными электродвигателями с редуктором. В связи с этим возникает проблема формирования управляющих сигналов g(t) приводов, обеспечивающих заданный закон изменения управляющих сил и моментов t . Если речь идет о приводах,

замкнутых по положению, что характерно для промышленных роботов с контурным управлением, то связь между g(t) и t

определяется уравнениями (3.14 ), из которых следует где WE (р) , Wq (р) — диагональные матрицы передаточных функций.

Из последнего уравнения видно, что задачу определения g(~) по виду t можно в общем случае решить только при-

118