Задания для самостоятельного решения

1. Построить кривые:

а) (архимедова спираль);

б) (лемниската Бернулли);

в) (трехлепестковая роза).

2. Записать в декартовых координатах уравнение линии и построить ее.

Контрольные вопросы

1. Какие кривые называются алгебраическими?

2. Какие соотношения связывают декартовые и полярные координаты точек?

3. Как вычисляется производная функции, заданной параметрически?

5. Вычисление площадей

Если фигура ограничена кривой, имеющей параметри­ческие уравнения , прямыми и осью , то площадь ее вычисляется по формуле

(13)

где пределы интегрирования находятся из уравнений на отрезке [ , ]). Формула (6.1) применима также для вычисления площади фигуры, ограниченной замк­нутой кривой (изменение параметра от , до должно соот­ветствовать обходу контура по часовой стрелке).

Пример 1. Вычислить площадь фигуры, ограниченной линиями, заданными уравнениями

Решение. Выразим из уравнений и , возведем их в квадрат и сложим. Получим

.

Это уравнение эллипса с полуосями равными 8 и 2. Данные линии изображаем на рисунке и заштриховываем искомую площадь (рис. 10). Найдем значения параметра , соответст­вующие точкам пересечения данных кривых. Для этого реша­ем уравнение и получаем (соответствует точке В) и (соответствует точке D). Искомая площадь , где - площадь фигуры ABCDE, a - площадь прямоугольника ABDE. По формуле (6.1) получаем

Для вычисления площади прямоугольника ABDE найдем координаты точек B и D. Получаем

Тогда и искомая площадь

Рис. 10

Пример 2. Вычислить площадь фигуры, ограниченной линиями, заданными уравнениями

Решение. Изобразим данные линии и заштрихуем искомую площадь (рис. 11). Найдем значения параметра , соответствующие точкам пересечения данных кривых. Для этого решаем уравнение или и получаем (соответствует точке B) и (соответствует точке C). Точке A соответствует значение параметра так как и

Площадь фигуры ABC находим как удвоенную площадь верхней половины ABD, интегрируя при этом в направлении возрастания от точки A до точки B:

x

Рис. 11

В полярных координатах площадь сектора, ограниченного дугой кривой и лучами и выражается интегралом

(14)

Пример 3. Найти площадь фигуры, лежащей вне окружности и ограниченной кривой

Решение. Так как функция имеет период то при изменении от 0 до радиус-вектор описывает два равных лепестка кривой. При этом допустимыми для являются те значения, при которых откуда

Следовательно, один из лепестков описывается при изменении от до Второй лепесток получается при изменении от до (рис. 12). Вырезая из лепестков части, принадлежащие кругу мы получим фигуру, площадь которой нужно определить. Ясно, что искомая площадь В свою очередь Точкам B и C соответствует значение полярного угла Найдем полярные координаты точки A пересечения данных кривых. Для этого решим уравнение т.е. Между 0 и находится только корень Таким образом, точке A, соответствует полярный угол

Рис. 12

Далее, пользуясь формулой (14) и найденными значениями полярных углов, определяем искомую площадь:

Пример 4. Вычислить площадь фигуры, ограниченной кривыми и (рис.13).

Решение. Так как при то первая кривая лежит в верхней полуплоскости и проходит через полюс Чтобы построить ее, перейдем в декартовые координаты, пользуясь соотношениями и Получаем Приведя это уравнение к каноническому виду, будем иметь Это уравнение окружности с центром (0, 1/2) и радиусом

Рис. 13

равным . Вторая кривая определена при т.е. при и также проходит через полюс Преобразуем уравнение второй кривой

и перейдем в декартовые координаты

Приведем полученное уравнение к каноническому виду:

Видно, что это уравнение окружности с центром и радиусом равным

Из вышесказанного следует, что полюс есть точка пересечения окружностей. Другая точка пересечения окружностей находится из решения уравнения или откуда Из рис.13 видно, что искомая площадь равна сумме площадей сегментов и причем сегменты примыкают друг к другу по лучу Дуга первого сегмента описывается концом полярного радиуса второй окружности при поэтому его площадь

Дуга второго сегмента описывается концом полярного радиуса первой окружности при поэтому его площадь

Таким образом, искомая площадь

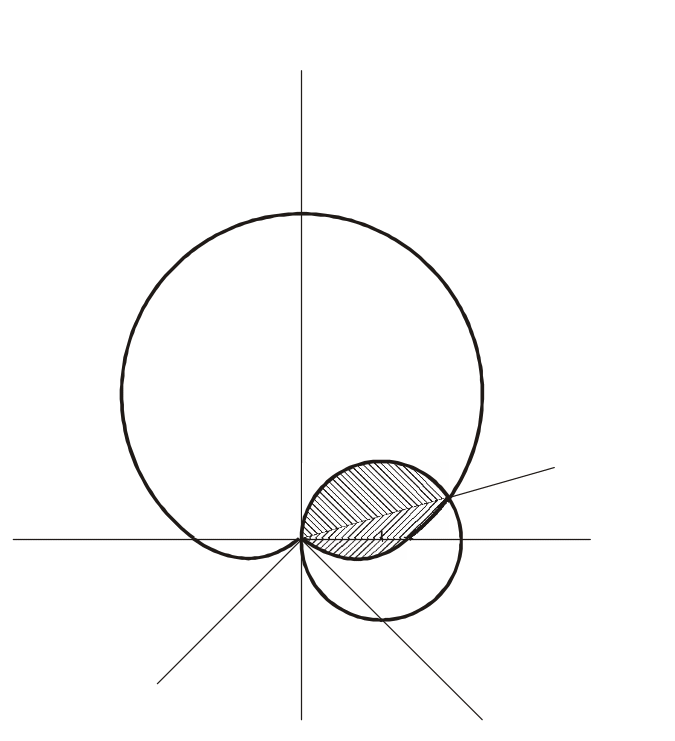
Пример 5. Найти площадь фигуры, ограниченной кривыми и (рис.14).

Решение. Определим область, в которой расположена первая кривая. Для этого решим неравенство Получаем Так как то в декартовых координатах уравнение первой кривой запишется следующим образом или в каноническом виде - это уравнение окружности с центром и радиусом, равным

Рис. 14

Окружность расположена в правой полуплоскости и проходит через полюс

Для построения второй кривой решаем неравенство Получаем Видно, что при граничных значениях полярного угла а при достигает максимального значения

Из вышеизложенного следует, что одной точкой пересечения данных кривых является полюс. Найдем остальные точки пересечения кривых. Для этого решим систему

Здесь указан диапазон углов, общих для обеих кривых. Приравнивая правые части уравнений, получаем

Из рисунка видно, что искомая площадь равна сумме площадей и двух сегментов, причем сегменты примыкают к друг другу по лучу Дуга первого сегмента описывается концом полярного радиуса при изменении полярного угла от до поэтому

.

Дуга второго сегмента описывается концом полярного радиуса при изменении полярного угла φ от π/12 до π/2, поэтому

Таким образом, искомая площадь равна

.

Задания для самостоятельного решения

1. Найти площадь фигуры, ограниченной астроидой

х = а cos³t, у = a sin³t.

2. Найти площадь фигуры, ограниченной аркой циклои­ды х = 2(t - sint), у = 2(l - cost) и прямой у = 2 (у>2).

3. Найти площадь фигуры, ограниченной эллипсом

х = 2cost, = 3sint и прямой .

4. Найти площадь фигуры, ограниченной пятилепестковой розой .

5. Найти площадь фигуры, ограниченной линиями и (рассмотреть два случая: r > 1 и r <1).

6. Найти площадь фигуры, ограниченной первым и вто­рым витками логарифмической спирали и лучом .

7. Найти площадь фигуры, ограниченной кардиоидой .