
Динамика точки и системы / Теоретическая механика
.pdf41
Коэффициент k называется коэффициентом трения качения.
Он определяется экспериментально, измеряется в системе СИ в метрах и определяет плечо пары (P; N ) при качении колеса.
16. Методика решения задач статики
Общая схема решения задач о равновесии тела (или конструкции, состоящей из нескольких тел) содержит несколько этапов.
Необходимо:
1.Выбрать тело (или конструкцию), исследование равновесия которого позволит определить требуемые величины. Начертить расчётную схему - упрощённый рисунок, на который вынесены лишь необходимые для решения линейные размеры и углы, а несущественные детали опущены.
2.Изобразить на схеме активные силы, заданные в условии задачи.
3.Если тело несвободно, отбросить наложенные на него механические связи, заменив их действие реакциями в соответствии с видами связей. После такой замены тело становится свободным.
4.Проверить выполнение необходимого условия статистической определимости задачи: число неизвестных, появившихся на расчётной схеме, не должно превышать числа уравнений равновесия для рассматриваемой системы сил.
5.Если задача статически определима, то, используя условия равновесия системы сил, составить систему уравнений равновесия и решить её.
При решении задачи рекомендуется действовать строго по описанной схеме.
42
КИНЕМАТИКА
В кинематике изучается движение твердых тел без учета их масс и действия на них сил. Движение тел происходит в пространстве и связано с изменением времени. В системе СИ расстояние измеряется в метрах, а время в секундах. Кинематическими характеристиками движения являются траектория, скорость и ускорение. Задать движение точки (или тела) - значит каким-то образом определить положение точки (или тела) в пространстве в любой момент времени.
Кинематика точки
Траектория – это множество последовательных положений точки в пространстве, то есть кривая, которую описывает точка при движении в пространстве.
Способы задания движения точки: Векторный способ задания движения точки.
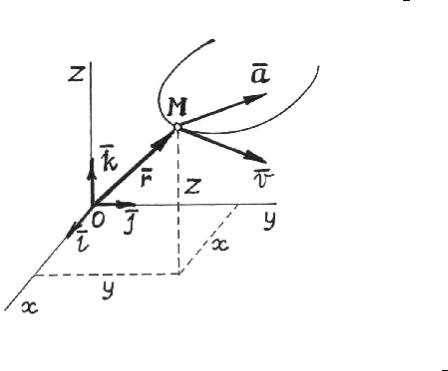
Положение точки в пространстве определяется радиус-вектором r , который меняется с течением времени (рис. 2.1).
Рис. 2.1
Закон движения точки задаётся, как функция изменения вектора r(t) за время от t0 до tk
ìr |
|
|
|
|
|
|
|
(t)= x(t)×i + y(t)× j + z(t)×k |
|||||||
ír |
|||||||
î |
t0 £ t £ tk |
||||||
Координатный способ задания движения.
Для того, чтобы движение было определено, можно задать закон движения, как систему функций изменения координат точки.

43
ìx(t)
ïïy(t)
í
ïz(t)
ï
î
=f1 (t)
=f2 (t)
=f3 (t)
Координатный способ представляет собой параметрическое задание траектории движения, где параметр – время t.
Зная закон движения, можно определить кинематические характеристики движения точки.
Скорость материальной точки.
V = ddtr = dxdt i + dydt j + dzdt k V =Vx (t)×i +Vy (t)× j +Vz (t)×k
Vx = x& , Vy = y& , |
Vz = z& |
V = V = 
 Vx2 +Vy2 +Vz2
Vx2 +Vy2 +Vz2
Вектор скорости V направлен по касательной к траектории в точке М.
Ускорение – первая производная от скорости. a = ddtV = dVdtx i + dVdty j + dVdtz k
Вектор a можно представить в виде проекций: a = ax (t)i + ay (t) j + az (t)k
Сравнивая эти векторные равенства, получим:
ax |
|
|
& |
= y |
& |
; az |
|
& |
|
= x = Vx ; ay |
= Vy |
= z = Vz |
|||||||
|
&& |
|
|
&& |
|
|
&& |
|
|
|
|
r |
|
|
|
|
|
|
|
|
|
= a = ax2 |
+ ay2 + az2 |
|
|
||||
|
|
a |
|
|
|||||
Скорость – векторная величина. Она изменяется по абсолютной величине и по направлению
Вектор ускорения лежит в плоскости, проходящей через две близкие касательные, проведенные практически в одной точке траектории. Предельное положение такой плоскости называется соприкасающейся плоскостью.
Таким образом, вектор ускорения точки лежит в соприкасающейся плоскости и направлен в сторону вогнутости траектории.
Естественный способ задания движения точки.
Естественный способ задания движения состоит в задании траектории точки, начала отсчета на траектории, положительного направления отсчета и закона движения по траектории.

44
Закон движения - это функция изменения естественной координаты S.
ìS = f (t)
íît0 £ t £ tk
S(t) – естественная координата.
Для определения естественной координаты S (рис. 2.2)задаются:
1)траектория (кривая L);
2)начальная точка траектории OS ;
3)положительное и отрицательное направления движения по траектории.
Естественная координата S - это длина дуги, отсчитываемая от на-
чальной точки OS до движущейся точки M на траектории. Если отсчёт длины дуги ведётся в положительном направлении, то естественная координата положительная, в противном случае - отрицательная (рис. 2.2).
Рис. 2.2
В каждой точке траектории определяются естественные оси координат τ , n,b .
Векторы τ , n,b - орты естественных осей координат; τ = n = b =1 .
Вектор τ направлен по касательной к траектории в положительном направлении изменения естественной координаты S, a вектор n перпендикулярен τ , лежит в соприкасающейся плоскости и направлен в сторону во-

45
гнутости траектории. Вектор b перпендикулярен τ и n и направлен так, что векторы τ , n,b расположены в пространстве аналогично единичным
r r
векторам i , j,k декартовой прямоугольной системы координат. Естественные оси координат перемещаются вместе с точкой. Длина дуги OM, взятой со знаком, определяет естественную координату.
Проекции векторов скорости и ускорения на естественные оси координат.
Вектор скорости точки M проецируется на ось, образованную единичным вектором τ .
r |
; |
& |
V = Vτ ×τ |
Vτ = S . |
Вектор ускорения проецируется на оси векторов τ и n a = aτ + an
aτ - касательное ускорение; an - нормальное ускорение.
Касательное ускорение характеризует изменение вектора скорости по величине. Нормальное ускорение характеризует изменение вектора скорости по направлению.
a = aττ + an n .
Проекции касательного и нормального ускорения равны
an = |
V 2 |
; |
|
ρM |
|||
|
|
aτ = V&τ = S&& ,
где ρM – радиус кривизны траектории
2.2).
Производная модуля скорости равна:
dV = d 
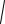 Vx2 +Vy2 +Vz2 dt dt
Vx2 +Vy2 +Vz2 dt dt
вданной точке (CM на рис.
=±aτ .
В зависимости от того, как выбрано положительное направление естественной координаты S, берётся знак “-“ или “+”.
На рис. 2.2 показан случай, когда проекция aτ отрицательная, а проекция скорости Vτ положительная.
Поступательное движение твёрдого тела.
Движение твердого тела называется поступательным, если любая прямая, проведенная в теле остается параллельной своему первоначальному положению.
Это наиболее простое движение твёрдого тела.
Вектор AB = const (рис. 2.3). Этот вектор постоянен по величине, т. к. тело абсолютно твердое, а по направлению – в силу определения посту-

46
пательного движения.
Рис. 2.3
Для точек A и B выполняется векторное равенство: rB = rA + AB . Дифференцируя его, получаем:
|
|
|
|
d( |
|
) |
|
|
||||
|
|
|
|
|
(т. к. |
AB |
= 0 ) и |
aA = aB . |
||||
VA = VB |
||||||||||||
dt |
|
|||||||||||
|
|
|
|
|
|
|
|
|||||
При поступательном движение твердого тела траектории всех точек одинаковы, скорости всех точек равны и ускорения также равны.
Вращательное движение твердого тела вокруг неподвижной оси.
Это такое движение, при котором хотя бы две точки, принадлежащие телу или неизменно с ним связанные, остаются неподвижными.
Рис. 2.4 |
Рис. 2.5 |

47
Ось, проходящая через две неподвижные точки, неподвижна и на-
зывается осью вращения твердого тела. На рис. 2.4 ось вращения Oz.
На рис. 2.5 показано сечение вращающегося тела, проходящее через точку M перпендикулярно оси вращения Oz.
Положение тела в пространстве определяется углом поворота ϕ (рис.
2.5).
Закон вращательного движения твёрдого тела вокруг неподвижной оси:
ϕ = f (t) , t0 £ t £ tk
Кинематические характеристики движения тела:
ϕ = ω - |
угловая скорость; |
& |
- угловое ускорение. |
ϕ = ω = ε |
|
&& & |
|
Векторы угловой скорости и углового ускорения ω и ε .
Эти векторы лежат на оси Oz и направлены так, что проекция на ось
Oz:
прozω = ω и прozε = ε (рис. 2.4).
При вращении твердого тела вокруг неподвижной оси каждая его точка движется по окружности, радиус которой равен расстоянию r от этой точки до оси вращения (рис. 2.5).
Скорости и ускорения точки определяют по формулам:
VM = ω ×OM
aM = aMτ + aMn
aMτ = ε ×OM
|
|
|
aMn |
|
= |
VM2 |
= ω 2 r |
|
|
|
|
||||
|
|
|
|
r |
|||
|
|
|
|
|
|
совпадают с направлением угло- |
|
|
|
|
|||||
Направления векторов VM и aM |
|||||||
вой скорости ω и углового ускорения ε соответственно. На рис. 2.4 и рис. 2.5 показан случай, когда ω и ε положительны.
Вектор скорости точки М можно определить по формуле Эйлера:
VM = ω ´OM
Движение твердого тела с одной неподвижной точкой (Сферическое движение).
Это такое движение, при котором одна точка, принадлежащая телу или неизменно с ним связанная, остается неподвижной (рис. 2.6).
Так как каждая точка тела движется по некоторой сферической поверхности, такое движение тела называют также сферическим.
В каждый момент времени при движении твёрдого тела с одной неподвижной точкой существует мгновенная ось вращения, проходящая через эту точку. Вдоль этой оси направлен вектор мгновенной угловой ско-

48
рости ω .
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 2.6 |
||||||||||
Скорость точки М определяется по формуле Эйлера |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
VM = |
ω |
× OM |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
& |
- угловое ускорение. |
|||||||||||||||
|
|||||||||||||||||||||||||||||
Вектор ε = ω |
|||||||||||||||||||||||||||||
Векторы |
|
|
и |
|
|
в общем случае неколлинеарны. |
|||||||||||||||||||||||
ω |
ε |
||||||||||||||||||||||||||||
Ускорение точки М равно: |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
aM = ε |
× |
|
+ |
ω |
× ( |
ω |
× |
|
) , |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
OM |
OM |
||||||||||||
ε |
× |
|
|
|
|
- вращательное ускорение; |
|||||||||||||||||||||||
OM |
|||||||||||||||||||||||||||||
|
ω |
× ( |
ω |
× |
|
) - |
осестремительное ускорение. |
||||||||||||||||||||||
|
OM |
||||||||||||||||||||||||||||
Общий случай движения твердого тела.
Для изучения такого движения в твёрдом теле фиксируется произвольная точка А, которая называется полюсом (рис. 2.7)
Движение твердого тела рассматривается, как сложение поступательного движения вместе с системой координат, взятой в точке А с осями Ax1, Ay1, Az1, параллельными осям Ox, Oy, Oz, и вращательного движения вокруг точки А, как неподвижной.
Определение скорости произвольной точки М:
rM = rA + AM .
Дифференцируем по времени
∙
r&M = r&A + AM .
Скорость точки M равна
VM = VA + ω × AM .
Определение ускорения точки M:
∙
aM = V&M = V&A + ω& × AM + ω × AM .

49
|
|
|
|
|
|
|
|
|
Рис. 2.7 |
||||||||||
|
|
& |
|
|
∙ |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Так как |
|
и AM = ω × AM , то |
|||||||||||||||||
ω = ε |
|||||||||||||||||||
|
|
|
|
|
aM = aA + ε |
× |
|
+ |
ω |
× ( |
ω |
× |
|
) . |
|||||
|
|
|
|
|
AM |
AM |
|||||||||||||
|
|
|
|
|
Сложное движение точки. |
||||||||||||||
Предположим, что некоторое тело движется относительно неподвижной (абсолютной) системы координат Oxyz (рис. 2.8). Свяжем жёстко с этим телом систему координат Ax1y1z1, которую назовём подвижной (относительной).
Рис. 2.8

50
Предположим, что материальная точка М движется относительно подвижной системы координат Ax1y1z1 по некоторой траектории Тотн. В этом случае по отношению к неподвижной системе координат Oxyz точка М совершает сложное движение, так как она движется вместе с телом (подвижной системой координат Ax1y1z1) и ещё сама движется по отношению к этому телу.
При изучении такого движения точки различают три вида движения этой точки.
Абсолютным движением точки М называется её движение по от-
ношению к неподвижной (абсолютной) системе координат. Скорость и ускорение точки в абсолютном движении называют соответственно абсо-
лютной скоростью и абсолютным ускорением и обозначают V и a . Относительным движением точки М называется её движение по
отношению к подвижной системе координат. Скорость и ускорение точки в относительном движении называются относительной скоростью и от-
носительным ускорением и обозначают Vr и ar .
Переносным движением называется движение подвижной системы координат по отношению к неподвижной. При этом движении подвижная система «переносит» вместе с собой множество неизменно связанных с ней точек.
Переносной скоростью и переносным ускорением называются скорости и ускорения той неизменно связанной с подвижной системой точки (В), с которой в данный момент времени совпадает движущаяся точка М, и обозначают Ve и ae .
Основные теоремы.
Теорема о скорости при сложном движении точки: вектор абсо-
лютной скорости равен геометрической сумме векторов относительной и переносной скоростей
V = Vr + Ve .
Теорема об ускорении при сложном движении точки (теорема Кориолиса): вектор абсолютного ускорения равен геометрической сумме векторов относительного, переносного и кориолисова ускорений
a = ar + ae + ak
Вектор ускорения Кориолиса определяется формулой ak = 2(ωe ×Vr ) .
и находится в соответствии с правилами вычисления векторного про-
изведения. |
|
|
Его абсолютная величина равна |
aкор |
= 2ωeVr sin α (рис. 2.9). |
При нахождении векторов ar |
и ae |
необходимо иметь в виду, что |
каждый из них может являться геометрической суммой нескольких составляющих, например касательного и нормального ускорений.
